沪科版(2012)初中数学八年级上册 12.2.5 一次函数的应用 同步习题(word解析版)
文档属性
| 名称 | 沪科版(2012)初中数学八年级上册 12.2.5 一次函数的应用 同步习题(word解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 140.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览




文档简介
第三单元
函
数
第11课时
一次函数及其应用
基础达标训练
1.
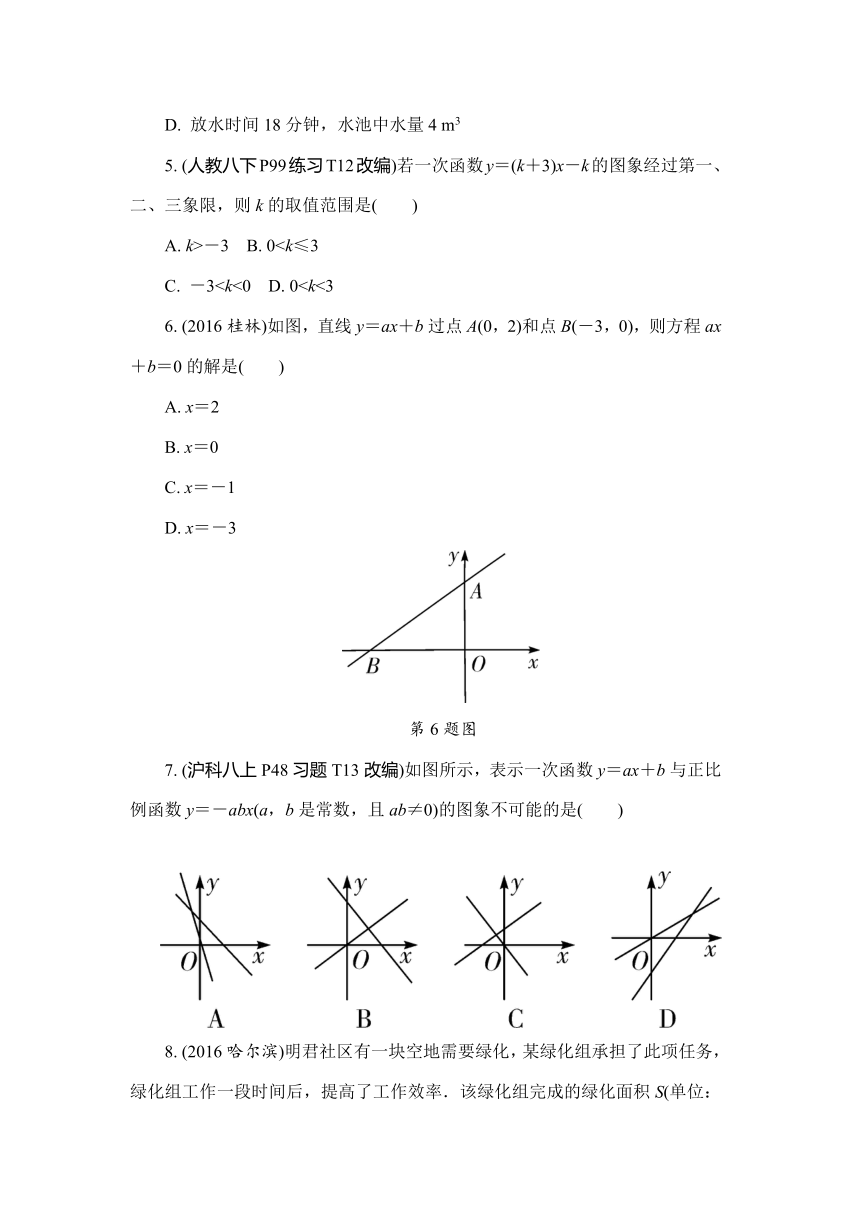
(2016郴州)当b<0时,一次函数y=x+b的图象大致是( )
2.
(沪科八上P61复习题A组T7(3)改编)函数y=-x的图象与y=2x+b的图象的交点在第四象限,则b的取值范围是( )
A.
b>0 B.
b=0 C.
b<0 D.
不能确定
3.
(2016玉林)关于直线l:y=kx+k(k≠0),下列说法不正确的是( )
A.
点(0,k)在l上
B.
l经过定点(-1,0)
C.
当k>0时,y随x的增大而增大
D.
l经过第一、二、三象限
4.
一蓄水池中有水40
m3,如果每分钟放出2
m3的水,水池里的水量与放水时间有如下关系:
放水时间(分)
1
2
3
4
…
水池中水量(m3)
38
36
34
32
…
下列数据中,满足此表格的是( )
A.
放水时间8分钟,水池中水量25
m3
B.
放水时间20分钟,水池中水量4
m3
C.
放水时间26分钟,水池中水量14
m3
D.
放水时间18分钟,水池中水量4
m3
5.
(人教八下P99练习T12改编)若一次函数y=(k+3)x-k的图象经过第一、二、三象限,则k的取值范围是( )
A.
k>-3
B.
0C.
-3D.
06.
(2016桂林)如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )
A.
x=2
B.
x=0
C.
x=-1
D.
x=-3
第6题图
7.
(沪科八上P48习题T13改编)如图所示,表示一次函数y=ax+b与正比例函数y=-abx(a,b是常数,且ab≠0)的图象不可能的是( )
8.
(2016哈尔滨)明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
A.
300
m2
B.
150
m2
C.
330
m2
D.
450
m2
第8题图
9.
(2016娄底改编)将直线y=2x+1向左平移3个单位长度后所得直线的解析式是________.
10.
(2016资阳)已知关于x的方程mx+3=4的解为x=1,则直线y=(m-2)x-3一定不经过第____象限.
11.
(2015广州)某水库的水位在5小时内持续上涨,初始的水位高度为6米,水位以每小时0.3米的速度匀速上升,则水库的水位高度y米与时间x小时(0≤x≤5)的函数关系式为________________.
12.
(沪科八上P39练习T3改编)直线y=-(k2+1)x+b经过点A(x1,y1)和B(x2,y2),当x1>x2时,y1________y2.(填“>”、“<”或“=”)
13.
(沪科八上P42练习T2改编)某地区采用分段计费的方法计算电费,月用电量x(度)与应缴纳电费y(元)之间的函数关系如图所示.那么当用电量为260度时,应缴电费________元.
第13题图
14.
(2016天津)若一次函数y=-2x+b(b为常数)的图象经过第二、三、四象限,则b的值可以是__________(写出一个即可).
15.
(2016东营)如图,直线y=x+b与直线y=kx+6交于点P(3,5),则关于x的不等式x+b>kx+6的解集是________.
第15题图
16.
(10分)(2016北京)如图,在平面直角坐标系xOy中,过点A(-6,0)的直线l1与直线l2:y=2x相交于点B(m,4).
(1)求直线l1的表达式;
(2)过动点P(n,0)且垂直于x轴的直线与l1,l2的交点分别为C,D,当点C位于点D上方时,写出n的取值范围.
第16题图
17.
(10分)(2016宜昌)如图,直线y=x+与两坐标轴分别交于A、B两点.
(1)求∠ABO的度数;
(2)过A的直线l交x轴正半轴于C,AB=AC,求直线l的函数解析式.
第17题图
18.
(10分)(2016三明)小李是某服装厂的一名工人,负责加工A,B两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工A型服装1件可得20元,加工B型服装1件可得12元.已知小李每天可加工A型服装4件或B型服装8件,设他每月加工A型服装的时间为x天,月收入为y元.
(1)求y与x的函数关系式;
(2)根据服装厂要求,小李每月加工A型服装数量应不少于B型服装数量的,那么他的月收入最高能达到多少元?
19.
(10分)(2016眉山)“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,顺风车行经营的A型车2015年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份A型车销售总额增加25%.
(1)求今年6月份A型车每辆售价多少元?(用列方程的方法解答)
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格如下表:
A型车
B型车
进货价格(元/辆)
1100
1400
销售价格(元/辆)
今年的销售价格
2400
能力提升拓展
1.
甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
①甲车的速度为50
km/h;②乙车用了3
h到达B城;③甲车出发4
h时,乙车追上甲车;④乙车出发后经过1
h或3
h两车相距50
km.
A.
1个
B.
2个
C.
3个
D.
4个
第1题图
第2题图
2.
如图,直线y=x+1分别与x轴、y轴相交于点A,B,以点A为圆心,AB长为半径画弧交x轴于点A1,再过点A1作x轴的垂线交直线于点B1,以点A为圆心,AB1长为半径画弧交x轴于点A2,…,按此作法进行下去,则点A8的坐标是( )
A.
(15,0)
B.
(16,0)
C.
(8,0)
D.
(8-1,0)
3.
(2016无锡)一次函数y=x-b与y=x-1的图象之间的距离等于3,则b的值为( )
A.-2或4
B.
2或-4
C.
4或-6
D.
-4或6
4.
(10分)(沪科八上P48习题T14改编)在如图所示的直角坐标系中,一次函数y=-2x+m的图象与y轴交于点B,与正比例函数y=2x的图象交于点P(2,n).
(1)求实数m,n的值;
(2)求△POB的面积.
第4题图
5.
(10分)(2016昆明)春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
6.
(12分)(2016南充)小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500
m,如图是小明和爸爸所走路程s(m)与步行时间t(min)的函数图象.
(1)直接写出小明所走路程s与时间t的函数关系式;
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早20
min到达公园,则小明在步行过程中停留的时间需作怎样的调整?
第6题图
答案
基础达标训练
1.
B 【解析】∵k=1>0,且b<0,∴函数图象过第一、三、四象限.
2.
C 【解析】∵直线y=-x经过第二、四象限,∴若两直线的交点在第四象限,则直线y=2x+b也经过第四象限,∵k=2>0,∴直线y=2x+b一定经过第一、三象限,从而直线y=2x+b经过第一、三、四象限,∴b<0.
3.
D 【解析】
选项
逐项分析
正误
A
令x=0,则y=k.∴点(0,k)在l上
√
B
当x=-1时,函数值y=-k+k=0,∴直线l经过定点(-1,0)
√
C
当k>0时,y随x的增大而增大
√
D
当且仅当k
是正数时;直线l经过第一、二、三象限,当k
是负数时,函数图象经过第二、三、四象限
×
4.
D 【解析】设蓄水量为y,时间为t,则可得y=40-2t.A.放水8分钟,水池中水量为24
m3,本选项错误;B.放水时间20分钟,水池中水量为0,本选项错误;C.放水时间26分钟,水池中水量为0,本选项错误;D.放水时间18分钟,水池中水量为4
m3,本选项正确,故选D.
5.
C 【解析】因为一次函数y=(k+3)x-k的图象经过第一、二、三象限,所以??-36.
D 【解析】一次函数y=ax+b与方程ax+b=0的关系是:方程的解就是一次函数的图象与x轴交点的横坐标.观察图象可知,点B(-3,0)就是直线与x轴的交点,所以方程的解就是x=-3.
7.
A 【解析】
选项
逐项分析
正误
A
由正比例函数图象得ab>0,由一次函数图象得a<0,b>0,矛盾,符合题意
√
B
由正比例函数图象得ab<0,由一次函数图象得a<0,b>0,成立,不符合题意
×
C
由正比例函数图象得ab>0,由一次函数图象得a>0,b>0,成立,不符合题意
×
D
由正比例函数图象得ab<0,由一次函数图象得a>0,b<0,成立,不符合题意
×
8.
B 【解析】设提高效率后对应的直线解析式为S=kt+b,由图可知,该直线经过(4,1200)和(5,1650)两点,代入得:,解得:,所以提高效率之后,S与t的函数解析式为:S=450t-600,则当t=2时,S=300,所以在前2个小时内,一共完成的绿化面积为300
m2,∴提高效率前每小时的绿化面积为:300÷2=150
m2.故选B.
9.
y=2x+7 【解析】根据直线的平移规律:左加右减,上加下减,可得到平移后的解析式为y=2(x+3)+1=2x+7.
10.
一
【解析】由题意知m+3=4,即m=1,将m=1代入一次函数有y=(1-2)x-3=-x-3,故函数图象一定不过第一象限.
11.
y=6+0.3x 【解析】根据题意可得:y=-6+0.3x(0≤x≤5).
12.
< 【解析】∵-(k2+1)<0,∴y随x的增大而减小,∴当x1>x2时,y1<y2.
13.
172 【解析】当x≥100时,设y与x之间的函数关系式为y=kx+b,由图象得,解得.∴y与x之间的函数关系式为y=0.7x-10,当x=260时,y=260×0.7-10=172元.
14.
-1(答案不唯一,满足b<0即可) 【解析】∵一次函数y=-2x+b的图象经过第二、三、四象限,∴b<0,故b的值可以是-1.
15.
x>3 【解析】由题图知:当x>3时,x+b>kx+6,即不等式x+b>kx+6的解集为x>3.
16.
解:(1)∵点B在直线l2上,
∴4=2m,
∴m=2,则B(2,4),
设直线l1的表达式为y=kx+b,
由A、B两点均在直线l1上得,
解得,
则l1的表达式为y=x+3;
(2)∵C、D分别为直线x=n与直线l1、l2的交点,
∴当点C位于点D的上方时,l1>l2,
结合图象可知,当x<2时,l1>l2成立,
∴n<2.
17.
解:(1)对于y=x+,令x=0,则y=.
∴点A的坐标为(0,),
∴OA=,
令y=0,则x=-1,
∴OB=1.
在Rt△AOB中,tan∠ABO==,
∴∠ABO=60°;
(2)∵在△ABC中,AB=AC,且AO⊥BC,
∴BO=CO,
∴点C的坐标为(1,0).
设直线l的函数解析式为y=kx+b(k、b为常数),
代入A、C两点的坐标,可得,
解得,
∴直线l的函数解析式为y=-x+.
18.
解:(1)由题意得:y=20×4x+12×8×(22-x)+900,
即y=-16x+3012;
(2)依题意得4x≥×8×(22-x),
解得,x≥12,
在y=-16x+3012中,
∵-16<0,
∴y随x的增大而减小.
∴当x=12时,y取最大值,此时y=-16×12+3012=2820元.
答:当小李每月加工A型服装12天时,月收入最高,可达2820元.
19.
解:(1)设去年6月份A型车每辆售价x元,则今年6月份每辆售价(x+400)元,
由题意得,=,
解得x=1600,
经检验,x=1600是原方程的根,且符合题意,
∴x+400=2000(元),
答:今年6月份A型车每辆售价为2000元;
(2)设今年7月份新进A型车m辆,则新进B型车(50-m)辆,获得的总利润为y元,
由题意得50-m≤2m,
解得m≥16,
y=(2000-1100)m+(2400-1400)(50-m)
=-100m+50000,
∵k=-100<0,
∴y随m的减少而增大,但m只能取整数,
∴当m取17时,可以获得最大利润.
答:当进货方案为:A型车17辆,B型车33辆时,才能使这批车获利最多.
能力提升拓展
1.
D 【解析】①v甲==50
km/h,正确;②乙车用了5-2=3
h到达B城,正确;③∵甲的解析式为y甲=50x,乙的解析式为y乙=100x-200,∴交点坐标为(4,200),即甲出发4
h时,乙车追上甲车,正确;④当|y甲-y乙|=50时,50x-(100x-200)=50或100x-200-50x=50,解得x1=3,x2=5,∴乙车出发时间为3-2=1h或5-2=3h,正确.
2.
A 【解析】对于直线y=x+1,当x=0时,y=1;当y=0时,x=-1,可得A(-1,0),B(0,1),AA1=AB===;AA2=AB1==2;AA3=AB2==2,则A1(-1,0),A2(2-1,0),A3(2-1,0),即A1(-1,0),A2(-1,0),A3(-1,0),从而可得点A8和横坐标为-1=16-1=15,则点A8的坐标为(15,0).
3.
D 【解析】∵直线y=x-1
与x轴的交点A的坐标为(
,0),与y轴的交点C的坐标为(0,-1),∴OA=,OC=1,直线y=x-b与直线y=x-1相距3,可分为两种情况:(1)如解图①,点B的坐标为(0,-b),则OB=-b,BC=1-b,易证△OAC∽△DBC,则=
,即=,解得b=-4;(2)如解图②,点F的坐标为(0,-b),则CF=b-1,易证△OAC∽△ECF,则=
,即=,解得b=6,故b=-4或6.
第3题解图
4.
解:(1)把P(2,n)代入y=2x得,n=2×2=4,
∴P点坐标为(2,4),
把P(2,4)代入y=-2x+m得,-4+m=4,解得m=8,
∴实数m=8,n=4;
(2)把x=0代入y=-2x+8得y=8,
∴B点坐标为(0,8),
∴S△POB=×8×2=8.
5.
解:(1)设甲种商品每件的进价为x元,乙种商品每件的进价为y元,
依题意得:,解得:,
答:甲种商品每件的进价为30元,乙种商品每件的进价为70元;
(2)设该商场购进甲种商品m件,则购进乙种商品(100-m)件,
由已知得:m≥4(100-m),
解得:m≥80.
设卖完A、B两种商品商场的利润为w,
则w=(40-30)m+(90-70)(100-m)=-10m+2000,
∵k=-10<0,
∴w随m的增大而减小,
∴当m=80时,w取最大值,最大利润为1200元.
∴100-m=20,
答:该商场获利最大的进货方案为购进甲商品80件,乙商品20件,最大利润为1200元.
6.
解:(1)小明所走路程s与时间t的函数关系式为:
(2)设爸爸走的路程s与时间t的函数关系式为s=kt+b,
由图象得,
解得,
则爸爸所走的路程s与时间t的函数关系式为s=30t+250.
由图象知,小明与爸爸第三次相遇是t>30
min,
根据题意得,
解得,
即小明出发37.5
min时与爸爸第三次相遇;
(3)当s=2500时,由题意得2500=30t+250,
解得t=75.
爸爸到达公园时t=75
min,小明到达公园时t=60
min,小明比爸爸早15
min到达公园,如果小明希望比爸爸早20
min到达公园,小明在步行过程中停留的时间应该减少5
min.
函
数
第11课时
一次函数及其应用
基础达标训练
1.
(2016郴州)当b<0时,一次函数y=x+b的图象大致是( )
2.
(沪科八上P61复习题A组T7(3)改编)函数y=-x的图象与y=2x+b的图象的交点在第四象限,则b的取值范围是( )
A.
b>0 B.
b=0 C.
b<0 D.
不能确定
3.
(2016玉林)关于直线l:y=kx+k(k≠0),下列说法不正确的是( )
A.
点(0,k)在l上
B.
l经过定点(-1,0)
C.
当k>0时,y随x的增大而增大
D.
l经过第一、二、三象限
4.
一蓄水池中有水40
m3,如果每分钟放出2
m3的水,水池里的水量与放水时间有如下关系:
放水时间(分)
1
2
3
4
…
水池中水量(m3)
38
36
34
32
…
下列数据中,满足此表格的是( )
A.
放水时间8分钟,水池中水量25
m3
B.
放水时间20分钟,水池中水量4
m3
C.
放水时间26分钟,水池中水量14
m3
D.
放水时间18分钟,水池中水量4
m3
5.
(人教八下P99练习T12改编)若一次函数y=(k+3)x-k的图象经过第一、二、三象限,则k的取值范围是( )
A.
k>-3
B.
0
-3
0
(2016桂林)如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )
A.
x=2
B.
x=0
C.
x=-1
D.
x=-3
第6题图
7.
(沪科八上P48习题T13改编)如图所示,表示一次函数y=ax+b与正比例函数y=-abx(a,b是常数,且ab≠0)的图象不可能的是( )
8.
(2016哈尔滨)明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
A.
300
m2
B.
150
m2
C.
330
m2
D.
450
m2
第8题图
9.
(2016娄底改编)将直线y=2x+1向左平移3个单位长度后所得直线的解析式是________.
10.
(2016资阳)已知关于x的方程mx+3=4的解为x=1,则直线y=(m-2)x-3一定不经过第____象限.
11.
(2015广州)某水库的水位在5小时内持续上涨,初始的水位高度为6米,水位以每小时0.3米的速度匀速上升,则水库的水位高度y米与时间x小时(0≤x≤5)的函数关系式为________________.
12.
(沪科八上P39练习T3改编)直线y=-(k2+1)x+b经过点A(x1,y1)和B(x2,y2),当x1>x2时,y1________y2.(填“>”、“<”或“=”)
13.
(沪科八上P42练习T2改编)某地区采用分段计费的方法计算电费,月用电量x(度)与应缴纳电费y(元)之间的函数关系如图所示.那么当用电量为260度时,应缴电费________元.
第13题图
14.
(2016天津)若一次函数y=-2x+b(b为常数)的图象经过第二、三、四象限,则b的值可以是__________(写出一个即可).
15.
(2016东营)如图,直线y=x+b与直线y=kx+6交于点P(3,5),则关于x的不等式x+b>kx+6的解集是________.
第15题图
16.
(10分)(2016北京)如图,在平面直角坐标系xOy中,过点A(-6,0)的直线l1与直线l2:y=2x相交于点B(m,4).
(1)求直线l1的表达式;
(2)过动点P(n,0)且垂直于x轴的直线与l1,l2的交点分别为C,D,当点C位于点D上方时,写出n的取值范围.
第16题图
17.
(10分)(2016宜昌)如图,直线y=x+与两坐标轴分别交于A、B两点.
(1)求∠ABO的度数;
(2)过A的直线l交x轴正半轴于C,AB=AC,求直线l的函数解析式.
第17题图
18.
(10分)(2016三明)小李是某服装厂的一名工人,负责加工A,B两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工A型服装1件可得20元,加工B型服装1件可得12元.已知小李每天可加工A型服装4件或B型服装8件,设他每月加工A型服装的时间为x天,月收入为y元.
(1)求y与x的函数关系式;
(2)根据服装厂要求,小李每月加工A型服装数量应不少于B型服装数量的,那么他的月收入最高能达到多少元?
19.
(10分)(2016眉山)“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,顺风车行经营的A型车2015年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份A型车销售总额增加25%.
(1)求今年6月份A型车每辆售价多少元?(用列方程的方法解答)
(2)该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格如下表:
A型车
B型车
进货价格(元/辆)
1100
1400
销售价格(元/辆)
今年的销售价格
2400
能力提升拓展
1.
甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
①甲车的速度为50
km/h;②乙车用了3
h到达B城;③甲车出发4
h时,乙车追上甲车;④乙车出发后经过1
h或3
h两车相距50
km.
A.
1个
B.
2个
C.
3个
D.
4个
第1题图
第2题图
2.
如图,直线y=x+1分别与x轴、y轴相交于点A,B,以点A为圆心,AB长为半径画弧交x轴于点A1,再过点A1作x轴的垂线交直线于点B1,以点A为圆心,AB1长为半径画弧交x轴于点A2,…,按此作法进行下去,则点A8的坐标是( )
A.
(15,0)
B.
(16,0)
C.
(8,0)
D.
(8-1,0)
3.
(2016无锡)一次函数y=x-b与y=x-1的图象之间的距离等于3,则b的值为( )
A.-2或4
B.
2或-4
C.
4或-6
D.
-4或6
4.
(10分)(沪科八上P48习题T14改编)在如图所示的直角坐标系中,一次函数y=-2x+m的图象与y轴交于点B,与正比例函数y=2x的图象交于点P(2,n).
(1)求实数m,n的值;
(2)求△POB的面积.
第4题图
5.
(10分)(2016昆明)春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
6.
(12分)(2016南充)小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500
m,如图是小明和爸爸所走路程s(m)与步行时间t(min)的函数图象.
(1)直接写出小明所走路程s与时间t的函数关系式;
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早20
min到达公园,则小明在步行过程中停留的时间需作怎样的调整?
第6题图
答案
基础达标训练
1.
B 【解析】∵k=1>0,且b<0,∴函数图象过第一、三、四象限.
2.
C 【解析】∵直线y=-x经过第二、四象限,∴若两直线的交点在第四象限,则直线y=2x+b也经过第四象限,∵k=2>0,∴直线y=2x+b一定经过第一、三象限,从而直线y=2x+b经过第一、三、四象限,∴b<0.
3.
D 【解析】
选项
逐项分析
正误
A
令x=0,则y=k.∴点(0,k)在l上
√
B
当x=-1时,函数值y=-k+k=0,∴直线l经过定点(-1,0)
√
C
当k>0时,y随x的增大而增大
√
D
当且仅当k
是正数时;直线l经过第一、二、三象限,当k
是负数时,函数图象经过第二、三、四象限
×
4.
D 【解析】设蓄水量为y,时间为t,则可得y=40-2t.A.放水8分钟,水池中水量为24
m3,本选项错误;B.放水时间20分钟,水池中水量为0,本选项错误;C.放水时间26分钟,水池中水量为0,本选项错误;D.放水时间18分钟,水池中水量为4
m3,本选项正确,故选D.
5.
C 【解析】因为一次函数y=(k+3)x-k的图象经过第一、二、三象限,所以??-3
D 【解析】一次函数y=ax+b与方程ax+b=0的关系是:方程的解就是一次函数的图象与x轴交点的横坐标.观察图象可知,点B(-3,0)就是直线与x轴的交点,所以方程的解就是x=-3.
7.
A 【解析】
选项
逐项分析
正误
A
由正比例函数图象得ab>0,由一次函数图象得a<0,b>0,矛盾,符合题意
√
B
由正比例函数图象得ab<0,由一次函数图象得a<0,b>0,成立,不符合题意
×
C
由正比例函数图象得ab>0,由一次函数图象得a>0,b>0,成立,不符合题意
×
D
由正比例函数图象得ab<0,由一次函数图象得a>0,b<0,成立,不符合题意
×
8.
B 【解析】设提高效率后对应的直线解析式为S=kt+b,由图可知,该直线经过(4,1200)和(5,1650)两点,代入得:,解得:,所以提高效率之后,S与t的函数解析式为:S=450t-600,则当t=2时,S=300,所以在前2个小时内,一共完成的绿化面积为300
m2,∴提高效率前每小时的绿化面积为:300÷2=150
m2.故选B.
9.
y=2x+7 【解析】根据直线的平移规律:左加右减,上加下减,可得到平移后的解析式为y=2(x+3)+1=2x+7.
10.
一
【解析】由题意知m+3=4,即m=1,将m=1代入一次函数有y=(1-2)x-3=-x-3,故函数图象一定不过第一象限.
11.
y=6+0.3x 【解析】根据题意可得:y=-6+0.3x(0≤x≤5).
12.
< 【解析】∵-(k2+1)<0,∴y随x的增大而减小,∴当x1>x2时,y1<y2.
13.
172 【解析】当x≥100时,设y与x之间的函数关系式为y=kx+b,由图象得,解得.∴y与x之间的函数关系式为y=0.7x-10,当x=260时,y=260×0.7-10=172元.
14.
-1(答案不唯一,满足b<0即可) 【解析】∵一次函数y=-2x+b的图象经过第二、三、四象限,∴b<0,故b的值可以是-1.
15.
x>3 【解析】由题图知:当x>3时,x+b>kx+6,即不等式x+b>kx+6的解集为x>3.
16.
解:(1)∵点B在直线l2上,
∴4=2m,
∴m=2,则B(2,4),
设直线l1的表达式为y=kx+b,
由A、B两点均在直线l1上得,
解得,
则l1的表达式为y=x+3;
(2)∵C、D分别为直线x=n与直线l1、l2的交点,
∴当点C位于点D的上方时,l1>l2,
结合图象可知,当x<2时,l1>l2成立,
∴n<2.
17.
解:(1)对于y=x+,令x=0,则y=.
∴点A的坐标为(0,),
∴OA=,
令y=0,则x=-1,
∴OB=1.
在Rt△AOB中,tan∠ABO==,
∴∠ABO=60°;
(2)∵在△ABC中,AB=AC,且AO⊥BC,
∴BO=CO,
∴点C的坐标为(1,0).
设直线l的函数解析式为y=kx+b(k、b为常数),
代入A、C两点的坐标,可得,
解得,
∴直线l的函数解析式为y=-x+.
18.
解:(1)由题意得:y=20×4x+12×8×(22-x)+900,
即y=-16x+3012;
(2)依题意得4x≥×8×(22-x),
解得,x≥12,
在y=-16x+3012中,
∵-16<0,
∴y随x的增大而减小.
∴当x=12时,y取最大值,此时y=-16×12+3012=2820元.
答:当小李每月加工A型服装12天时,月收入最高,可达2820元.
19.
解:(1)设去年6月份A型车每辆售价x元,则今年6月份每辆售价(x+400)元,
由题意得,=,
解得x=1600,
经检验,x=1600是原方程的根,且符合题意,
∴x+400=2000(元),
答:今年6月份A型车每辆售价为2000元;
(2)设今年7月份新进A型车m辆,则新进B型车(50-m)辆,获得的总利润为y元,
由题意得50-m≤2m,
解得m≥16,
y=(2000-1100)m+(2400-1400)(50-m)
=-100m+50000,
∵k=-100<0,
∴y随m的减少而增大,但m只能取整数,
∴当m取17时,可以获得最大利润.
答:当进货方案为:A型车17辆,B型车33辆时,才能使这批车获利最多.
能力提升拓展
1.
D 【解析】①v甲==50
km/h,正确;②乙车用了5-2=3
h到达B城,正确;③∵甲的解析式为y甲=50x,乙的解析式为y乙=100x-200,∴交点坐标为(4,200),即甲出发4
h时,乙车追上甲车,正确;④当|y甲-y乙|=50时,50x-(100x-200)=50或100x-200-50x=50,解得x1=3,x2=5,∴乙车出发时间为3-2=1h或5-2=3h,正确.
2.
A 【解析】对于直线y=x+1,当x=0时,y=1;当y=0时,x=-1,可得A(-1,0),B(0,1),AA1=AB===;AA2=AB1==2;AA3=AB2==2,则A1(-1,0),A2(2-1,0),A3(2-1,0),即A1(-1,0),A2(-1,0),A3(-1,0),从而可得点A8和横坐标为-1=16-1=15,则点A8的坐标为(15,0).
3.
D 【解析】∵直线y=x-1
与x轴的交点A的坐标为(
,0),与y轴的交点C的坐标为(0,-1),∴OA=,OC=1,直线y=x-b与直线y=x-1相距3,可分为两种情况:(1)如解图①,点B的坐标为(0,-b),则OB=-b,BC=1-b,易证△OAC∽△DBC,则=
,即=,解得b=-4;(2)如解图②,点F的坐标为(0,-b),则CF=b-1,易证△OAC∽△ECF,则=
,即=,解得b=6,故b=-4或6.
第3题解图
4.
解:(1)把P(2,n)代入y=2x得,n=2×2=4,
∴P点坐标为(2,4),
把P(2,4)代入y=-2x+m得,-4+m=4,解得m=8,
∴实数m=8,n=4;
(2)把x=0代入y=-2x+8得y=8,
∴B点坐标为(0,8),
∴S△POB=×8×2=8.
5.
解:(1)设甲种商品每件的进价为x元,乙种商品每件的进价为y元,
依题意得:,解得:,
答:甲种商品每件的进价为30元,乙种商品每件的进价为70元;
(2)设该商场购进甲种商品m件,则购进乙种商品(100-m)件,
由已知得:m≥4(100-m),
解得:m≥80.
设卖完A、B两种商品商场的利润为w,
则w=(40-30)m+(90-70)(100-m)=-10m+2000,
∵k=-10<0,
∴w随m的增大而减小,
∴当m=80时,w取最大值,最大利润为1200元.
∴100-m=20,
答:该商场获利最大的进货方案为购进甲商品80件,乙商品20件,最大利润为1200元.
6.
解:(1)小明所走路程s与时间t的函数关系式为:
(2)设爸爸走的路程s与时间t的函数关系式为s=kt+b,
由图象得,
解得,
则爸爸所走的路程s与时间t的函数关系式为s=30t+250.
由图象知,小明与爸爸第三次相遇是t>30
min,
根据题意得,
解得,
即小明出发37.5
min时与爸爸第三次相遇;
(3)当s=2500时,由题意得2500=30t+250,
解得t=75.
爸爸到达公园时t=75
min,小明到达公园时t=60
min,小明比爸爸早15
min到达公园,如果小明希望比爸爸早20
min到达公园,小明在步行过程中停留的时间应该减少5
min.
