人教版九年级数学上册导学案:24.3正多边形和圆(含答案)
文档属性
| 名称 | 人教版九年级数学上册导学案:24.3正多边形和圆(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 131.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览

文档简介
人教版九年级数学上册导学案
第二十四章
圆
24.3正多边形和圆
【学习目标】
1.了解正多边形的有关概念.
2.理解并掌握正多边形半径和边长、边心距、中心角之间的关系,
3.熟练掌握正三边形、正方形、正六边形的有关计算。
【课前预习】
1.在圆内接四边形ABCD中,若,则(
)
A.40
B.50
C.130
D.150
2.已知和有相同的外心,,则的度数是(
).
A.80°
B.100°
C.80°或100°
D.不能确定.
3.圆内接四边形中,已知,则的对角(
?)
A.
B.
C.
D.
4.下列说法正确的有(
)
①不在同一条直线上的三点确定一个圆;②平分弦的直径垂直于弦;③在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等;④圆内接平行四边形是矩形.
A.1个
B.2个
C.3个
D.4个
5.下列是有关圆的一些结论,其中正确的是(
)
A.任意三点可以确定一个圆
B.相等的圆心角所对的弧相等
C.平分弦的直径垂直于弦
D.圆内接四边形对角互补
6.下列有关圆的一些结论:①任意三点确定一个圆;②相等的圆心角所对的弧相等;③平分弦的直径垂直于弦;并且平分弦所对的弧,④圆内接四边形对角互补.其中错误的结论有(
)
A.1个
B.2个
C.3个
D.4个
7.已知⊙O的半径为1,弦AB长为1,则弦AB所对的圆周角为(
)
A.60°
B.30°
C.60°和120°
D.30°和150°
8.下列命题是假命题的是(
)
A.点A(2,1)与点B(-2,-1)关于原点对称
B.不等式组的解集是空集
C.对角线互相垂直且相等的四边形是正方形
D.圆内接四边形的对角互补
9.下列命题是真命题的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.菱形一定有外接圆
C.三角形的重心是三条边的垂直平分线的交点
D.六边形的内角和是外角和的2倍
10.在正五边形的外接圆中,任一边所对的圆周角的度数为(
)
A.
B.
C.
D.或
【学习探究】
自主学习
阅读课本,完成下列问题
1.
如果一个多边形的
顶点都在
圆上,这个多边形叫做圆的内接多边形,这个圆叫做这个多边形的
.
2.什么叫正多边形?
3.举例说出生活中常见的正多边形.
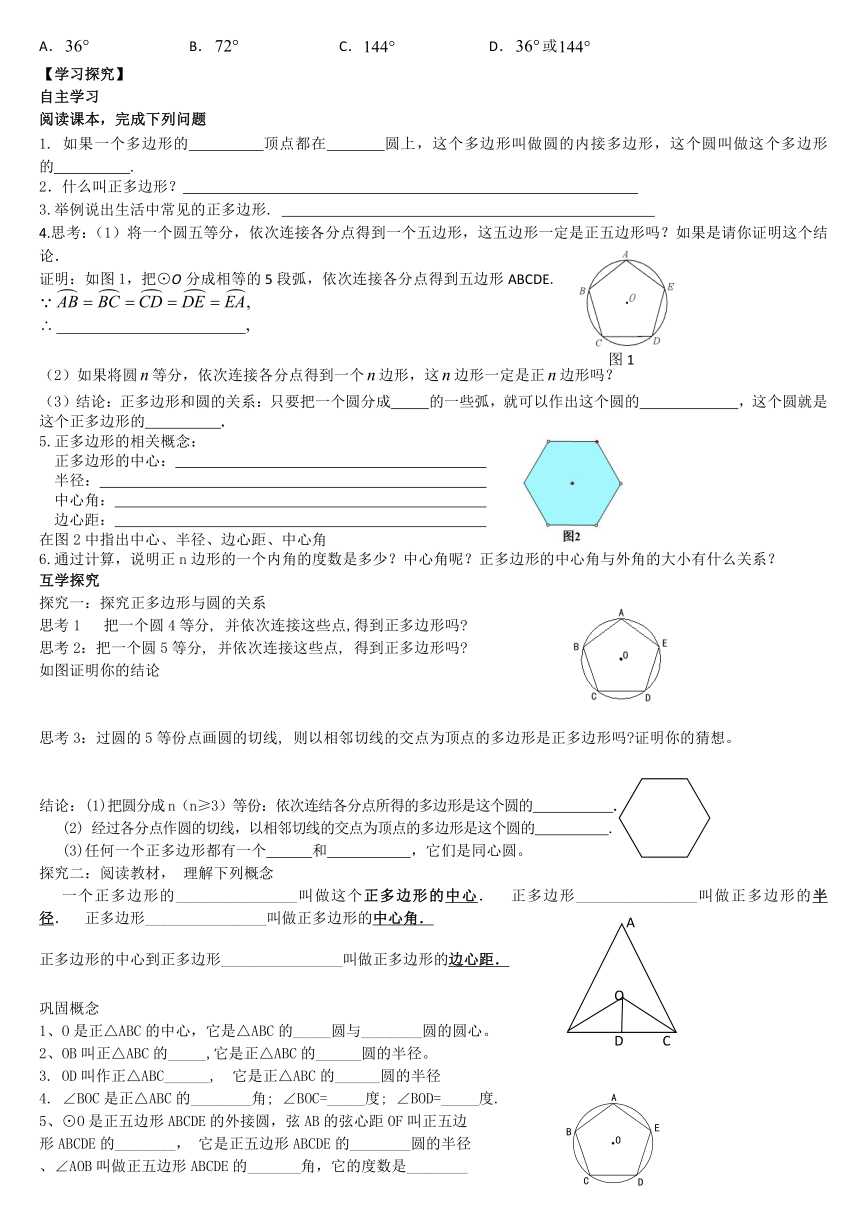
4.思考:(1)将一个圆五等分,依次连接各分点得到一个五边形,这五边形一定是正五边形吗?如果是请你证明这个结论.
证明:如图1,把⊙O分成相等的5段弧,依次连接各分点得到五边形ABCDE.
(2)如果将圆等分,依次连接各分点得到一个边形,这边形一定是正边形吗?
(3)结论:正多边形和圆的关系:只要把一个圆分成
的一些弧,就可以作出这个圆的
,这个圆就是这个正多边形的
.
5.正多边形的相关概念:
正多边形的中心:
半径:
中心角:
边心距:
在图2中指出中心、半径、边心距、中心角
6.通过计算,说明正n边形的一个内角的度数是多少?中心角呢?正多边形的中心角与外角的大小有什么关系?
互学探究
探究一:探究正多边形与圆的关系
思考1
把一个圆4等分,
并依次连接这些点,得到正多边形吗?
思考2:把一个圆5等分,
并依次连接这些点,
得到正多边形吗?
如图证明你的结论
思考3:过圆的5等份点画圆的切线,
则以相邻切线的交点为顶点的多边形是正多边形吗?证明你的猜想。
结论:(1)把圆分成n(n≥3)等份:依次连结各分点所得的多边形是这个圆的
.
(2)
经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的
.
(3)任何一个正多边形都有一个
和
,它们是同心圆。
探究二:阅读教材,
理解下列概念
一个正多边形的________________叫做这个正多边形的中心.?正多边形________________叫做正多边形的半径.?正多边形________________叫做正多边形的中心角.?
正多边形的中心到正多边形________________叫做正多边形的边心距.?
巩固概念
1、O是正△ABC的中心,它是△ABC的_____圆与________圆的圆心。
2、OB叫正△ABC的_____,它是正△ABC的______圆的半径。
3.
OD叫作正△ABC______,
它是正△ABC的______圆的半径
4.
∠BOC是正△ABC的________角;
∠BOC=_____度;
∠BOD=_____度.
5、⊙O是正五边形ABCDE的外接圆,弦AB的弦心距OF叫正五边
形ABCDE的________,
它是正五边形ABCDE的________圆的半径
、∠AOB叫做正五边形ABCDE的_______角,它的度数是________
7、图中正六边形ABCDEF的中心角是_______;它的度数是_________;
8、你发现正六边形ABCDEF的半径与边长具有什么数量关系?为什么?
结论:(1)正n边形的中心角=
;外角与中心角
(2)设正n边形的边长为a,半径为R,则周长为L=
.边心距r与a和R的关系式是
,正n边形的面积为
。
例题
例1
有一个亭子它的地基是半径为4m的正六边形,
求地基的周长和面积(精确到0.1平方米).
例2、如图所示,已知⊙O的周长等于6cm,求以它的半径为边长的正六边形ABCDEF的面积.
【课后练习】
1.在圆内接四边形ABCD中,若∠A:∠B:∠C=2:3:4,则∠D=(
)
A.90°
B.120°
C.150°
D.240°
2.圆的内接四边形ABCD的四个内角之比∠A:∠B:∠C:∠D的可能的值是(
)
A.1:2:3:4
B.1:3:2:4
C.1:4:2:3
D.1:2:4:3
3.已知AB是⊙O半径OC的垂直平分线,点P是劣弧上的点,则的度数为(
)
A.135°
B.130°
C.120°
D.110°
4.下列说法中,正确的是(
)
A.弦是直径
B.相等的弦所对的弧相等
C.圆内接四边形的对角互补
D.三个点确定一个圆
5.在圆内接四边形ABCD中,若,则(
)
A.
B.
C.
D.
6.下列命题中,真命题的个数是( )
①平分弦的直径垂直于弦;②圆内接平行四边形必为矩形;③90°的圆周角所对的弦是直径;④任意三个点确定一个圆;⑤同弧所对的圆周角相等.
A.5
B.4
C.3
D.2
7.已知:正方形ABCD内接于⊙O,点P是⊙O上不同于点B、C的任意一点,则∠BPC的度数是
.
A.45°
B.90°
C.135°
D.45°或135°
8.下列说法正确的有(
)
①平分弦的直径垂直于弦.②半圆所对的圆周角是直角.③一条弧所对的圆周角等于它所对的圆心角的一半.④在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等.⑤圆内接平行四边形是矩形.
A.1个
B.2个
C.3个
D.4个
9.△ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是(
)
A.80°
B.160°
C.80°或20°
D.80°或100°
10.已知圆内接四边形ABCD中,∠A:∠B:∠C=1:2:3,则∠D的大小是(
)
A.45°
B.60°
C.90°
D.135°
11.若△ABC
内接于⊙O
,∠BOC=80°,则∠BAC=____________.
12.一条弦所对的圆心角是120°,那么它所对的圆周角为_____.
13.下列图形中:①平行四边形;②矩形;③菱形;④正方形;⑤等腰梯形.其中四个顶点在同一圆上的有___________(只填序号即可).
14.四边形ABCD是某个圆的内接四边形,若,则__________.
15.在中,,,在外有一点,且,则的度数是__________.
【参考答案】
【课前预习】
1.C
2.C
3.D
4.B
5.D
6.C
7.D
8.C
9.D
10.D
【课后练习】
1.A
2.D
3.C
4.C
5.C
6.C
7.D
8.C
9.D
10.C
11.40或140
12.60°或120°
13.②④⑤
14.100°
15.135°、45°
第二十四章
圆
24.3正多边形和圆
【学习目标】
1.了解正多边形的有关概念.
2.理解并掌握正多边形半径和边长、边心距、中心角之间的关系,
3.熟练掌握正三边形、正方形、正六边形的有关计算。
【课前预习】
1.在圆内接四边形ABCD中,若,则(
)
A.40
B.50
C.130
D.150
2.已知和有相同的外心,,则的度数是(
).
A.80°
B.100°
C.80°或100°
D.不能确定.
3.圆内接四边形中,已知,则的对角(
?)
A.
B.
C.
D.
4.下列说法正确的有(
)
①不在同一条直线上的三点确定一个圆;②平分弦的直径垂直于弦;③在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等;④圆内接平行四边形是矩形.
A.1个
B.2个
C.3个
D.4个
5.下列是有关圆的一些结论,其中正确的是(
)
A.任意三点可以确定一个圆
B.相等的圆心角所对的弧相等
C.平分弦的直径垂直于弦
D.圆内接四边形对角互补
6.下列有关圆的一些结论:①任意三点确定一个圆;②相等的圆心角所对的弧相等;③平分弦的直径垂直于弦;并且平分弦所对的弧,④圆内接四边形对角互补.其中错误的结论有(
)
A.1个
B.2个
C.3个
D.4个
7.已知⊙O的半径为1,弦AB长为1,则弦AB所对的圆周角为(
)
A.60°
B.30°
C.60°和120°
D.30°和150°
8.下列命题是假命题的是(
)
A.点A(2,1)与点B(-2,-1)关于原点对称
B.不等式组的解集是空集
C.对角线互相垂直且相等的四边形是正方形
D.圆内接四边形的对角互补
9.下列命题是真命题的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.菱形一定有外接圆
C.三角形的重心是三条边的垂直平分线的交点
D.六边形的内角和是外角和的2倍
10.在正五边形的外接圆中,任一边所对的圆周角的度数为(
)
A.
B.
C.
D.或
【学习探究】
自主学习
阅读课本,完成下列问题
1.
如果一个多边形的
顶点都在
圆上,这个多边形叫做圆的内接多边形,这个圆叫做这个多边形的
.
2.什么叫正多边形?
3.举例说出生活中常见的正多边形.
4.思考:(1)将一个圆五等分,依次连接各分点得到一个五边形,这五边形一定是正五边形吗?如果是请你证明这个结论.
证明:如图1,把⊙O分成相等的5段弧,依次连接各分点得到五边形ABCDE.
(2)如果将圆等分,依次连接各分点得到一个边形,这边形一定是正边形吗?
(3)结论:正多边形和圆的关系:只要把一个圆分成
的一些弧,就可以作出这个圆的
,这个圆就是这个正多边形的
.
5.正多边形的相关概念:
正多边形的中心:
半径:
中心角:
边心距:
在图2中指出中心、半径、边心距、中心角
6.通过计算,说明正n边形的一个内角的度数是多少?中心角呢?正多边形的中心角与外角的大小有什么关系?
互学探究
探究一:探究正多边形与圆的关系
思考1
把一个圆4等分,
并依次连接这些点,得到正多边形吗?
思考2:把一个圆5等分,
并依次连接这些点,
得到正多边形吗?
如图证明你的结论
思考3:过圆的5等份点画圆的切线,
则以相邻切线的交点为顶点的多边形是正多边形吗?证明你的猜想。
结论:(1)把圆分成n(n≥3)等份:依次连结各分点所得的多边形是这个圆的
.
(2)
经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的
.
(3)任何一个正多边形都有一个
和
,它们是同心圆。
探究二:阅读教材,
理解下列概念
一个正多边形的________________叫做这个正多边形的中心.?正多边形________________叫做正多边形的半径.?正多边形________________叫做正多边形的中心角.?
正多边形的中心到正多边形________________叫做正多边形的边心距.?
巩固概念
1、O是正△ABC的中心,它是△ABC的_____圆与________圆的圆心。
2、OB叫正△ABC的_____,它是正△ABC的______圆的半径。
3.
OD叫作正△ABC______,
它是正△ABC的______圆的半径
4.
∠BOC是正△ABC的________角;
∠BOC=_____度;
∠BOD=_____度.
5、⊙O是正五边形ABCDE的外接圆,弦AB的弦心距OF叫正五边
形ABCDE的________,
它是正五边形ABCDE的________圆的半径
、∠AOB叫做正五边形ABCDE的_______角,它的度数是________
7、图中正六边形ABCDEF的中心角是_______;它的度数是_________;
8、你发现正六边形ABCDEF的半径与边长具有什么数量关系?为什么?
结论:(1)正n边形的中心角=
;外角与中心角
(2)设正n边形的边长为a,半径为R,则周长为L=
.边心距r与a和R的关系式是
,正n边形的面积为
。
例题
例1
有一个亭子它的地基是半径为4m的正六边形,
求地基的周长和面积(精确到0.1平方米).
例2、如图所示,已知⊙O的周长等于6cm,求以它的半径为边长的正六边形ABCDEF的面积.
【课后练习】
1.在圆内接四边形ABCD中,若∠A:∠B:∠C=2:3:4,则∠D=(
)
A.90°
B.120°
C.150°
D.240°
2.圆的内接四边形ABCD的四个内角之比∠A:∠B:∠C:∠D的可能的值是(
)
A.1:2:3:4
B.1:3:2:4
C.1:4:2:3
D.1:2:4:3
3.已知AB是⊙O半径OC的垂直平分线,点P是劣弧上的点,则的度数为(
)
A.135°
B.130°
C.120°
D.110°
4.下列说法中,正确的是(
)
A.弦是直径
B.相等的弦所对的弧相等
C.圆内接四边形的对角互补
D.三个点确定一个圆
5.在圆内接四边形ABCD中,若,则(
)
A.
B.
C.
D.
6.下列命题中,真命题的个数是( )
①平分弦的直径垂直于弦;②圆内接平行四边形必为矩形;③90°的圆周角所对的弦是直径;④任意三个点确定一个圆;⑤同弧所对的圆周角相等.
A.5
B.4
C.3
D.2
7.已知:正方形ABCD内接于⊙O,点P是⊙O上不同于点B、C的任意一点,则∠BPC的度数是
.
A.45°
B.90°
C.135°
D.45°或135°
8.下列说法正确的有(
)
①平分弦的直径垂直于弦.②半圆所对的圆周角是直角.③一条弧所对的圆周角等于它所对的圆心角的一半.④在同圆或等圆中,如果两条弦相等,那么他们所对的圆周角相等.⑤圆内接平行四边形是矩形.
A.1个
B.2个
C.3个
D.4个
9.△ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是(
)
A.80°
B.160°
C.80°或20°
D.80°或100°
10.已知圆内接四边形ABCD中,∠A:∠B:∠C=1:2:3,则∠D的大小是(
)
A.45°
B.60°
C.90°
D.135°
11.若△ABC
内接于⊙O
,∠BOC=80°,则∠BAC=____________.
12.一条弦所对的圆心角是120°,那么它所对的圆周角为_____.
13.下列图形中:①平行四边形;②矩形;③菱形;④正方形;⑤等腰梯形.其中四个顶点在同一圆上的有___________(只填序号即可).
14.四边形ABCD是某个圆的内接四边形,若,则__________.
15.在中,,,在外有一点,且,则的度数是__________.
【参考答案】
【课前预习】
1.C
2.C
3.D
4.B
5.D
6.C
7.D
8.C
9.D
10.D
【课后练习】
1.A
2.D
3.C
4.C
5.C
6.C
7.D
8.C
9.D
10.C
11.40或140
12.60°或120°
13.②④⑤
14.100°
15.135°、45°
同课章节目录
