人教版九年级数学下册课件-26.1.2 反比例函数的图象和性质(22张)
文档属性
| 名称 | 人教版九年级数学下册课件-26.1.2 反比例函数的图象和性质(22张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 23:22:45 | ||
图片预览






文档简介
第1课时
26.1.2 反比例函数的图象与性质
x
y
O
查学诊断
y = 3x-1
y = 2x2
y =
2x
3
y =
x
1
y = 3x
y =
3
2x
y =
1
3x
y =
x
1
(1)下列函数中哪些是正比例函数?哪些是反比例?
2.还记得一次函数的图像与性质吗?
3、还记得二次函数的图像与性质吗?
4、如何画函数的图像?
提问:反比例函数的图像与性质又如何呢?
这节课开始我们来一起探究吧。
函数图象画法
描点法
列
表
描
点
连
线
1.会用描点法画反比例函数的图象
2.结合图象分析并掌握反比例函数的性质
3.通过画图象,进一步培养“描点法”画图的能力和方法,并提高对函数图象的分析能力.同时尝试用类比和特殊到一般的思路方法,归纳反比例函数一些性质特征
4由图象的画法和分析,体验数学活动中的探索性和创造性,感受数学美,并通过图象的直观教学激发学习兴趣.
我们已知道,一次函数y=kx+b(k≠0)的图象是一条直线,二次函数是一条抛物线,那么反比例函数y=k/x (k为常数且k≠0)的图象是什么样呢?有什么性质?这节课我们大家一起来学习反比例函数的图像和性质!
x
画出反比例函数 和 的函数图象
y =
x
6
y =
x
6
列
表
描
点
连
线
y =
x
6
y =
x
6
注意:①列表时自变量取值要均匀和对称
②x≠0
③选整数较好计算
④描点
导学施教
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =
x
6
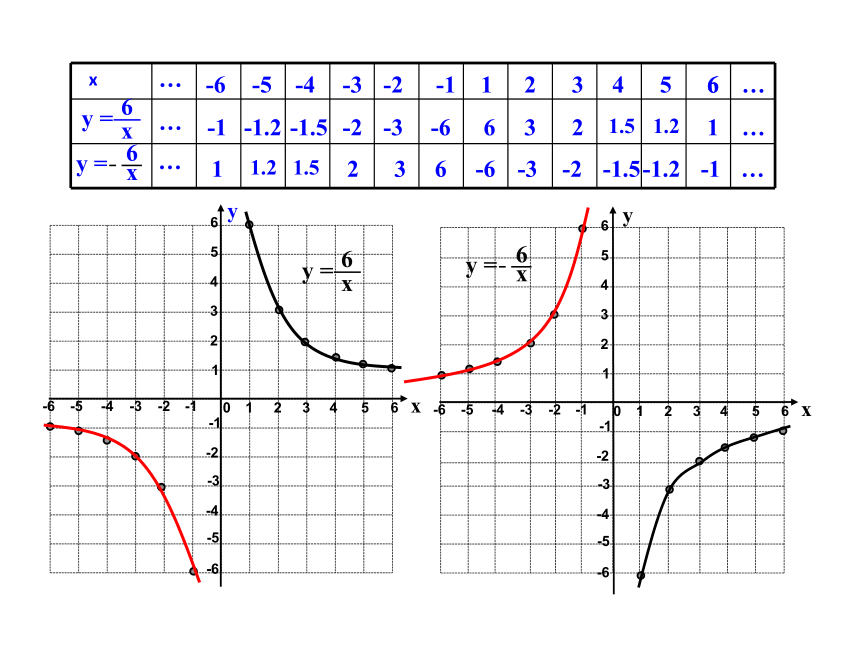
你认为作反比例函数图象时应注意哪些问题?
1.列表时,选取的自变量的值,既要易于计算,又要便于描点,尽量多取一些数值(取互为相反数的一对一对的数),多描一些点,这样既可以方便连线,又可以使图象精确.
2.描点时要严格按照表中所列的对应值描点,绝对不能把点的位置描错.
3.线连时一定要养成按自变量从小到大的顺序依次画线,连线时必须用光滑的曲线连接各点,不能用折线连接.
4.图象是延伸的,注意不要画的有明确端点.
5.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.
【解析】
1.列表:
2.描点:
3.连线:
x
…
-8
-4
-3
-2
-1
…
1
2
3
4
8
…
…
-1
-2
-4
-8
8
4
2
1
以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.
用光滑的曲线顺次连接各点,就可得到图象.
1.画出函数y = — 的图象
-4
x
【跟踪训练】
5
1
2
3
4
6
-4
-1
-2
.
-3
-5
-6
1
2
4
5
6
3
-6
-5
-1
-3
-4
-2
0
.
.
.
y
x
.
.
.
.
y = —
-4
x
-7
-7
-8
7 8
.
7
8
.
.
.
-8
1
2
3
4
5
6
-4
-1
-2
.
-3
-5
-6
1
2
4
5
6
3
-6
-5
-1
-3
-4
-2
0
.
.
.
.
.
y
x
.
.
.
.
y=—
4
x
.
x
y
0
1
3
2
4
5
6
1
2
3
4
5
6
-6
-6
-5
-3
-4
-1
-2
-4
-5
-3
-2
-1
.
.
.
.
.
.
.
.
y = —
-4
x
.
位置:
函数 的两 支曲线分别位于第一、三象限内.
函数 的两支曲线分别位于第二、四象限内.
形状:
反比例函数的图象是由两支曲线组成的.
因此称反比例函数的图象为双曲线.
【结论】
反比例函数 的图象在哪两个象限,由什么确定?
当k>0时,两支曲线分别位于第一,三象限内;
当k<0时,两支曲线分别位于第二,四象限内.
答:由k的符号决定.
K>0
K<0
当k>0时,函数图象
的两个分支分别在第
一、三象限,在每个
象限内,y随x的增大
而减小.
当k<0时,函数图象
的两个分支分别在第
二、四象限,在每个
象限内,y随x的增大
而增大.
1.反比例函数的图象是双曲线;
2.图象性质见下表:
图
象
性质
y=
归纳:反比例函数的图象和性质:
A.
x
y
o
B.
x
y
o
D.
x
y
o
C.
x
y
o
1.反比例函数y= - 的图象大致是( )
D
练测促学
-5 /x
2.如图,函数y=k/x和y=-kx+1(k≠0)在同一坐标系内
的图象大致是( )
D
.
.
.
.
3.已知反比例函数 的图象在第二、四象限,那么一次函数y=kx-k的图象经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
C
4.甲乙两地相距100km,一辆汽车从甲地开往乙地,把汽
车到达乙地所用的时间y(h)表示为汽车的平均速度x(km/h)
的函数,则这个函数的图象大致是( )
C
提示:在实际问题中图象只有一支曲线.
5.若关于x,y的函数 图象位于第一、三象限,则k的取值范围是_________.
k>-1
请大家围绕以下三个问题小结本节课
① 什么是反比例函数?
② 反比例函数的图象是什么样子的?
③ 反比例函数
的性质是什么?
( 是常数, 0)
y =
x
k
k
k
≠
反馈延伸
课堂小结
K>0
K<0
当k>0时,函数图象
的两个分支分别在第
一、三象限,在每个
象限内,y随x的增大
而减小.
当k<0时,函数图象
的两个分支分别在第
二、四象限,在每个
象限内,y随x的增大
而增大.
图象性质见下表:
图
象
性质
y=
归纳:反比例函数的图象和性质:
作业:习题26.1、 3
26.1.2 反比例函数的图象与性质
x
y
O
查学诊断
y = 3x-1
y = 2x2
y =
2x
3
y =
x
1
y = 3x
y =
3
2x
y =
1
3x
y =
x
1
(1)下列函数中哪些是正比例函数?哪些是反比例?
2.还记得一次函数的图像与性质吗?
3、还记得二次函数的图像与性质吗?
4、如何画函数的图像?
提问:反比例函数的图像与性质又如何呢?
这节课开始我们来一起探究吧。
函数图象画法
描点法
列
表
描
点
连
线
1.会用描点法画反比例函数的图象
2.结合图象分析并掌握反比例函数的性质
3.通过画图象,进一步培养“描点法”画图的能力和方法,并提高对函数图象的分析能力.同时尝试用类比和特殊到一般的思路方法,归纳反比例函数一些性质特征
4由图象的画法和分析,体验数学活动中的探索性和创造性,感受数学美,并通过图象的直观教学激发学习兴趣.
我们已知道,一次函数y=kx+b(k≠0)的图象是一条直线,二次函数是一条抛物线,那么反比例函数y=k/x (k为常数且k≠0)的图象是什么样呢?有什么性质?这节课我们大家一起来学习反比例函数的图像和性质!
x
画出反比例函数 和 的函数图象
y =
x
6
y =
x
6
列
表
描
点
连
线
y =
x
6
y =
x
6
注意:①列表时自变量取值要均匀和对称
②x≠0
③选整数较好计算
④描点
导学施教
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =
x
6
你认为作反比例函数图象时应注意哪些问题?
1.列表时,选取的自变量的值,既要易于计算,又要便于描点,尽量多取一些数值(取互为相反数的一对一对的数),多描一些点,这样既可以方便连线,又可以使图象精确.
2.描点时要严格按照表中所列的对应值描点,绝对不能把点的位置描错.
3.线连时一定要养成按自变量从小到大的顺序依次画线,连线时必须用光滑的曲线连接各点,不能用折线连接.
4.图象是延伸的,注意不要画的有明确端点.
5.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.
【解析】
1.列表:
2.描点:
3.连线:
x
…
-8
-4
-3
-2
-1
…
1
2
3
4
8
…
…
-1
-2
-4
-8
8
4
2
1
以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.
用光滑的曲线顺次连接各点,就可得到图象.
1.画出函数y = — 的图象
-4
x
【跟踪训练】
5
1
2
3
4
6
-4
-1
-2
.
-3
-5
-6
1
2
4
5
6
3
-6
-5
-1
-3
-4
-2
0
.
.
.
y
x
.
.
.
.
y = —
-4
x
-7
-7
-8
7 8
.
7
8
.
.
.
-8
1
2
3
4
5
6
-4
-1
-2
.
-3
-5
-6
1
2
4
5
6
3
-6
-5
-1
-3
-4
-2
0
.
.
.
.
.
y
x
.
.
.
.
y=—
4
x
.
x
y
0
1
3
2
4
5
6
1
2
3
4
5
6
-6
-6
-5
-3
-4
-1
-2
-4
-5
-3
-2
-1
.
.
.
.
.
.
.
.
y = —
-4
x
.
位置:
函数 的两 支曲线分别位于第一、三象限内.
函数 的两支曲线分别位于第二、四象限内.
形状:
反比例函数的图象是由两支曲线组成的.
因此称反比例函数的图象为双曲线.
【结论】
反比例函数 的图象在哪两个象限,由什么确定?
当k>0时,两支曲线分别位于第一,三象限内;
当k<0时,两支曲线分别位于第二,四象限内.
答:由k的符号决定.
K>0
K<0
当k>0时,函数图象
的两个分支分别在第
一、三象限,在每个
象限内,y随x的增大
而减小.
当k<0时,函数图象
的两个分支分别在第
二、四象限,在每个
象限内,y随x的增大
而增大.
1.反比例函数的图象是双曲线;
2.图象性质见下表:
图
象
性质
y=
归纳:反比例函数的图象和性质:
A.
x
y
o
B.
x
y
o
D.
x
y
o
C.
x
y
o
1.反比例函数y= - 的图象大致是( )
D
练测促学
-5 /x
2.如图,函数y=k/x和y=-kx+1(k≠0)在同一坐标系内
的图象大致是( )
D
.
.
.
.
3.已知反比例函数 的图象在第二、四象限,那么一次函数y=kx-k的图象经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
C
4.甲乙两地相距100km,一辆汽车从甲地开往乙地,把汽
车到达乙地所用的时间y(h)表示为汽车的平均速度x(km/h)
的函数,则这个函数的图象大致是( )
C
提示:在实际问题中图象只有一支曲线.
5.若关于x,y的函数 图象位于第一、三象限,则k的取值范围是_________.
k>-1
请大家围绕以下三个问题小结本节课
① 什么是反比例函数?
② 反比例函数的图象是什么样子的?
③ 反比例函数
的性质是什么?
( 是常数, 0)
y =
x
k
k
k
≠
反馈延伸
课堂小结
K>0
K<0
当k>0时,函数图象
的两个分支分别在第
一、三象限,在每个
象限内,y随x的增大
而减小.
当k<0时,函数图象
的两个分支分别在第
二、四象限,在每个
象限内,y随x的增大
而增大.
图象性质见下表:
图
象
性质
y=
归纳:反比例函数的图象和性质:
作业:习题26.1、 3
