2020-2021学年第一学期安徽省涡阳县王元中学第三次月考数学试卷(word版,含答案)
文档属性
| 名称 | 2020-2021学年第一学期安徽省涡阳县王元中学第三次月考数学试卷(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 284.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 14:49:18 | ||
图片预览


文档简介
2020-2021
学年度第一学期九年级质量检测试卷(三)
数学(沪科版)
注意事项∶
1.你拿到的试卷满分为
150
分,考试时间为120分钟。
2.本试卷包括“试题卷”和“答题卷”两部分。“试题卷”共4页,“答题卷”共6页。
3.请务必在“答题卷”上答题,在“试题卷”上答题是无效的。
4.
考试结束后,请将“试题卷”和“答题卷”一并交回。
一、选择题(
本大题共
10
小题,每小题4分,共40
分)
1.反比例函数(x
>0)的图像位于(
)
A.第一象限
B.第二象限
C.第二象限
D.第二象限
2.如图,直线l1/l2,/l3,直线AC和DF被l1,l2,l3所截,AB=5,BC=6,EF=4,则DE的长为(
)
A.2
B.3
C.4
B.
3.如图,在
Rt△ABC中,∠C=90°,sinB=0.5,若AC=6,则BC的长为(
)
A.8
B.12
C.
B.
4.抛物线y=-3x?-1是由抛物线y=-3(x+1)?+1怎样平移得到的(
)
A.左移1个单位上移2个单位
B.左移1个单位下移2
个单位
B.右移1个单位上移2个单位
D.右移1个单位下移2
个单位
5.若,则的值为(
)
A.1
B.
C.
B.
6.如图,A,B,C是3×1的正方形网格中的三个格点,则
tan∠ABC的值为(
)
A.1
B.
C.
D.
7.△ABC中,∠A,∠B都是锐角,且
sinA
=,cosB=则△ABC
的形状是(
)
A.直角三角形
B.
钝角三角形
C.锐角三角形
D.
锐角三角形或钝角三角形
8.如图,正方形ABCD的边长是2,E是
BC的中点,连接
BD、AE
相交于点O,则OD的长为(
)
A.
B.
C.
D.5
9.有以下命题∶
①如果线段d是线段a,b,c
的第四比例项,则有;
②如果点C是线段
AB
的中点,那么AC
是AB、BC的比例中项;
③如果点C是线段AB的黄金分割点,且AC>BC,那么AC是AB与BC的比例中项;
④如果点C是线段
AB的黄金分割点,AC>BC,且AB=2,则AC=-1.
其中正确的判断有(
)
A.
②④
B.①②③④
C.
①③④
D.②③④
10.如图,△ABC中,∠ACB=90°,∠A=30°,AB=16,点P是斜边AB上任意一点,过点P作
PQ⊥AB,垂足为P,交边AC(或边
CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致是(
)
二、填空题(本大题共4
小题,每小题5分,共20
分)
11.抛物线y
=
(x+2)2-1的顶点坐标为___________。
12.如图,在△ABC中,点D、E分别是
AB、AC的中点,若△ADE
的面积为
4,则△ABC
的面积为___________。
13.已知
tan(α+15°)=,则锐角a
的度数为___________。
14.如图AD是△ABC的中线,E是AD上一点,且A=AD,CE的延长线
AB
交于点
F,若
AF=2,则AB=___________。
三、(本大题共2
小题,每小题8
分,满分
16
分)
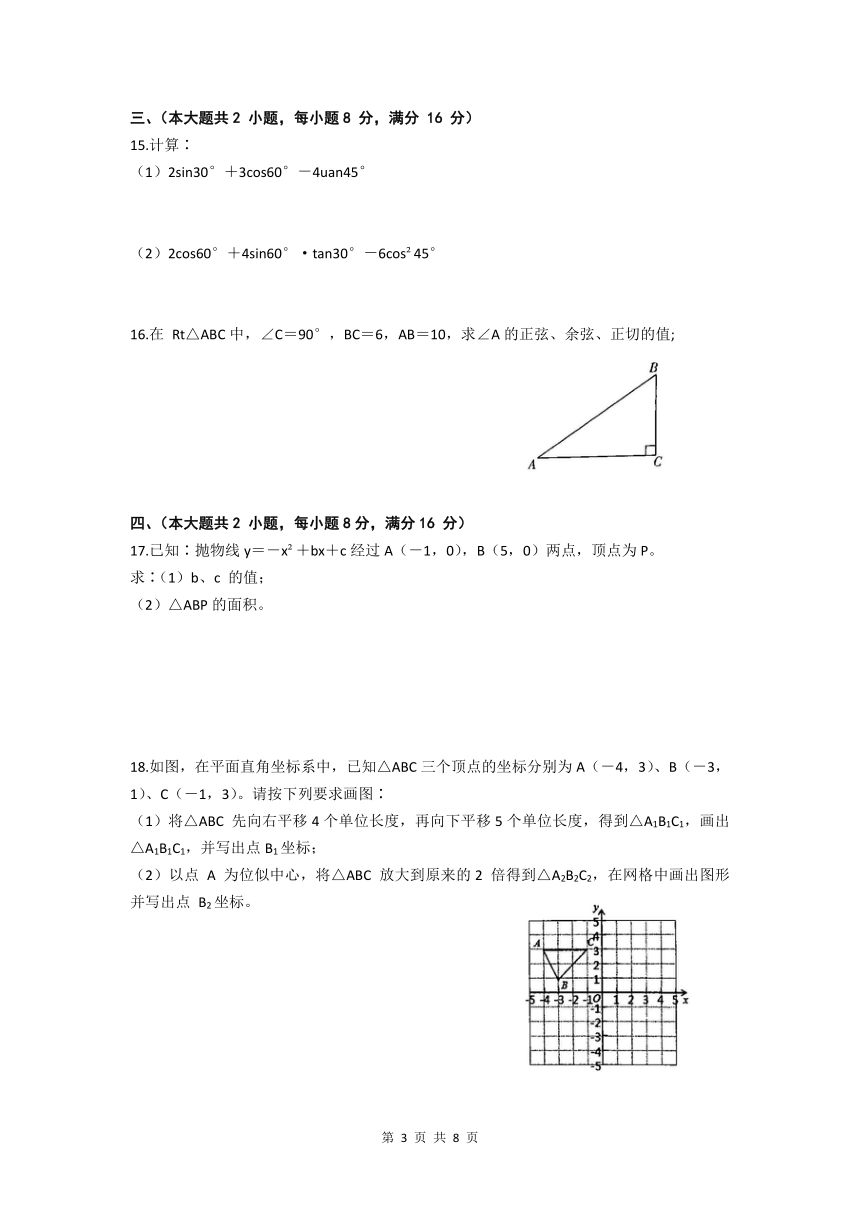
15.计算∶
(1)2sin30°+3cos60°-4uan45°
(2)2cos60°+4sin60°·tan30°-6cos?45°
16.在
Rt△ABC中,∠C=90°,BC=6,AB=10,求∠A的正弦、余弦、正切的值;
四、(本大题共2
小题,每小题8分,满分16
分)
17.已知∶抛物线y=-x?+bx+c经过A(-1,0),B(5,0)两点,顶点为P。
求∶(1)b、c
的值;
(2)△ABP的面积。
18.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-4,3)、B(-3,1)、C(-1,3)。请按下列要求画图∶
(1)将△ABC
先向右平移4个单位长度,再向下平移5个单位长度,得到△A1B1C1,画出△A1B1C1,并写出点B1坐标;
(2)以点
A
为位似中心,将△ABC
放大到原来的2
倍得到△A2B2C2,在网格中画出图形并写出点
B2坐标。
五、(本大题共2
小题,每小题
10
分,满分20分)
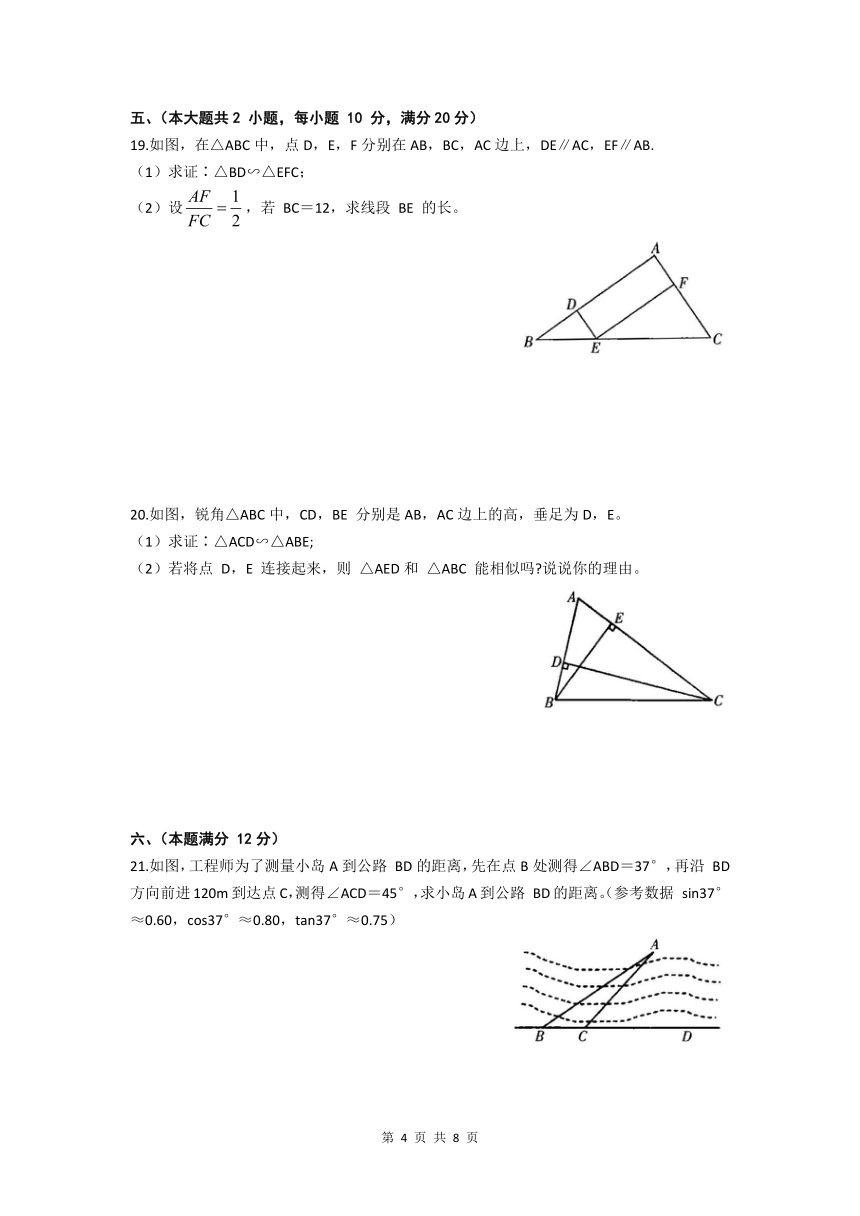
19.如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证∶△BD∽△EFC;
(2)设,若
BC=12,求线段
BE
的长。
20.如图,锐角△ABC中,CD,BE
分别是AB,AC边上的高,垂足为D,E。
(1)求证∶△ACD∽△ABE;
(2)若将点
D,E
连接起来,则
△AED和
△ABC
能相似吗?说说你的理由。
六、(本题满分
12分)
21.如图,工程师为了测量小岛A到公路
BD的距离,先在点B处测得∠ABD=37°,再沿
BD方向前进120m到达点C,测得∠ACD=45°,求小岛A到公路
BD的距离。(参考数据
sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
七、(本题满分12
分)
22.如图,在△ABC中,AC=AB,AB⊥AC,点E是边AC的中点,AF⊥BE于点F。
(1)求证∶AE?=FE·
BE;
(2)求∠AFC的大小。
八、(本题满分14
分)
23.某医药研究所研发了一种新药,试验药效时发现∶1.5
小时内,血液中含药量y(微克)与时间x(小时)的关系可近似地用二次函数y=ax?+bx表示;1.5
小时后(包括1.5
小时),y
与
x可近似地用反比例函数y=(k>0)表示,部分实验数据如表∶
时间
x(小时)
0.2
1
1.8
含药量
y(微克)
7.2
20
12.5
(1)求a、b及k的值;
(2)服药后几小时血液中的含药量达到最大值?最大值为多少?
(3)如果每毫升血液中含药量不少于10
微克时治疗疾病有效,那么成人按规定剂量服用该药一次后能维持多长的有效时间.(
≈1.41,精确到0.1
小时)
2020-2021学年度第一学期九年级数学质量检测试卷(三)
参考答案
(沪科版)
1-5.DDCDB
6-10.ACACD
11、(-2,-1)
12、16
13、15
14.10
原式
15、解:(1)
原式
16、解:∵在Rt△ABC中,∠C=90°,BC=6,AB=10,
∴AC=
∴
cosA
tanA
17、解:(1)设抛物线的解析式为y=-(x+1)(x-5),所以y=-x2+4x+5,
所以b=4,c=5;
(2)y=-x2+4x+5=-(x-2)2+9,P点坐标为(2,9),
所以△ABP的面积=×6×9=27
18【解答】解:(1)△A1B1C1如图所示,B1点的坐标为(1,-4);
(2)△A2B2C2如图所示,点B2的坐标为(-2,-1);
19【解答】(1)证明:∵DE∥AC,
∴∠DEB=∠FCE,
∴EF∥AB,∴∠DBE=∠FEC.
∴△BDEAEFC;
(2)解:∵EF∥AB.
∴
∵EC=BC-BE=12-B,
∴
解得:BE=4。
20、证明:(1)∵CD,BE分别是AB,AC边上的高,∴∠ADC=∠AEB=90°.
∵∠A=∠A,
∴△ACD∽△ABE
(2)连接DE,
∵△ACD∽△ABE,
∴AD:AE=AC:AB.
∴AD:AC=AE:AB.
∵∠A=∠A.
∴△AED∽△ABC
21.解:如图,过A作AE⊥CD垂足为E,设AE=x米,
在Rt△ABE中,tanB=,BE=,
在Rt△ABE中,tan∠ACD=
∴CE=
∵BC=BE-CE,
∴
解得:x=360。
答:小岛A到公路BD的距离为360米。
22.(1)证明:
∵AB⊥AC,AF⊥BE,
∴∠EAB=∠EFA=90°.
∵∠AEF=∠BEA
∴△AEF∽△BEA
∴
∴AE2=FE·BE
(2)解:∵E是AC的中点,
∴AE=CE,
∵AE2=FE·BE
∴CE2=FE·BE
∴
又∵∠CEF=∠BEC,
∴△CEF∽△BEC,
∴∠EFC=∠ECB.
∵AB=AC,∠BAC=90°,
∴∠ACB=45°
∴∠EFC=45°
∵∠AFE=90°
∴∠AFC=90°+45°=135°
23.解:(1)设1.5小时内,血液中含药量y(微克)与时间x(小时)的关系为y=ax2+bx,
根据表格得:
解得:a=-20,b=40,
1.5小时后(包括1.5小时),y与x可近似地用反比例函数y=(k>0),根据表格得:
k=1.8×12.5=22.5
∴a=-20
b=40
k=22.5;
(2)由(1)知y=-20x2+40x,
∵y=-20(x-1)2+20.
∴服药后1小时血液中的含药量达到最大值,最大值为20微克;
(3)当y=10时,10=-20x2+40x,或10=
解得:x=1-或x=1+(x>1.5,不合题意舍去),x=2.25
∴成人按规定剂量服用该药一次后能维持2.25-(1-)<2.0小时的有效时间
学年度第一学期九年级质量检测试卷(三)
数学(沪科版)
注意事项∶
1.你拿到的试卷满分为
150
分,考试时间为120分钟。
2.本试卷包括“试题卷”和“答题卷”两部分。“试题卷”共4页,“答题卷”共6页。
3.请务必在“答题卷”上答题,在“试题卷”上答题是无效的。
4.
考试结束后,请将“试题卷”和“答题卷”一并交回。
一、选择题(
本大题共
10
小题,每小题4分,共40
分)
1.反比例函数(x
>0)的图像位于(
)
A.第一象限
B.第二象限
C.第二象限
D.第二象限
2.如图,直线l1/l2,/l3,直线AC和DF被l1,l2,l3所截,AB=5,BC=6,EF=4,则DE的长为(
)
A.2
B.3
C.4
B.
3.如图,在
Rt△ABC中,∠C=90°,sinB=0.5,若AC=6,则BC的长为(
)
A.8
B.12
C.
B.
4.抛物线y=-3x?-1是由抛物线y=-3(x+1)?+1怎样平移得到的(
)
A.左移1个单位上移2个单位
B.左移1个单位下移2
个单位
B.右移1个单位上移2个单位
D.右移1个单位下移2
个单位
5.若,则的值为(
)
A.1
B.
C.
B.
6.如图,A,B,C是3×1的正方形网格中的三个格点,则
tan∠ABC的值为(
)
A.1
B.
C.
D.
7.△ABC中,∠A,∠B都是锐角,且
sinA
=,cosB=则△ABC
的形状是(
)
A.直角三角形
B.
钝角三角形
C.锐角三角形
D.
锐角三角形或钝角三角形
8.如图,正方形ABCD的边长是2,E是
BC的中点,连接
BD、AE
相交于点O,则OD的长为(
)
A.
B.
C.
D.5
9.有以下命题∶
①如果线段d是线段a,b,c
的第四比例项,则有;
②如果点C是线段
AB
的中点,那么AC
是AB、BC的比例中项;
③如果点C是线段AB的黄金分割点,且AC>BC,那么AC是AB与BC的比例中项;
④如果点C是线段
AB的黄金分割点,AC>BC,且AB=2,则AC=-1.
其中正确的判断有(
)
A.
②④
B.①②③④
C.
①③④
D.②③④
10.如图,△ABC中,∠ACB=90°,∠A=30°,AB=16,点P是斜边AB上任意一点,过点P作
PQ⊥AB,垂足为P,交边AC(或边
CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致是(
)
二、填空题(本大题共4
小题,每小题5分,共20
分)
11.抛物线y
=
(x+2)2-1的顶点坐标为___________。
12.如图,在△ABC中,点D、E分别是
AB、AC的中点,若△ADE
的面积为
4,则△ABC
的面积为___________。
13.已知
tan(α+15°)=,则锐角a
的度数为___________。
14.如图AD是△ABC的中线,E是AD上一点,且A=AD,CE的延长线
AB
交于点
F,若
AF=2,则AB=___________。
三、(本大题共2
小题,每小题8
分,满分
16
分)
15.计算∶
(1)2sin30°+3cos60°-4uan45°
(2)2cos60°+4sin60°·tan30°-6cos?45°
16.在
Rt△ABC中,∠C=90°,BC=6,AB=10,求∠A的正弦、余弦、正切的值;
四、(本大题共2
小题,每小题8分,满分16
分)
17.已知∶抛物线y=-x?+bx+c经过A(-1,0),B(5,0)两点,顶点为P。
求∶(1)b、c
的值;
(2)△ABP的面积。
18.如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-4,3)、B(-3,1)、C(-1,3)。请按下列要求画图∶
(1)将△ABC
先向右平移4个单位长度,再向下平移5个单位长度,得到△A1B1C1,画出△A1B1C1,并写出点B1坐标;
(2)以点
A
为位似中心,将△ABC
放大到原来的2
倍得到△A2B2C2,在网格中画出图形并写出点
B2坐标。
五、(本大题共2
小题,每小题
10
分,满分20分)
19.如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证∶△BD∽△EFC;
(2)设,若
BC=12,求线段
BE
的长。
20.如图,锐角△ABC中,CD,BE
分别是AB,AC边上的高,垂足为D,E。
(1)求证∶△ACD∽△ABE;
(2)若将点
D,E
连接起来,则
△AED和
△ABC
能相似吗?说说你的理由。
六、(本题满分
12分)
21.如图,工程师为了测量小岛A到公路
BD的距离,先在点B处测得∠ABD=37°,再沿
BD方向前进120m到达点C,测得∠ACD=45°,求小岛A到公路
BD的距离。(参考数据
sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
七、(本题满分12
分)
22.如图,在△ABC中,AC=AB,AB⊥AC,点E是边AC的中点,AF⊥BE于点F。
(1)求证∶AE?=FE·
BE;
(2)求∠AFC的大小。
八、(本题满分14
分)
23.某医药研究所研发了一种新药,试验药效时发现∶1.5
小时内,血液中含药量y(微克)与时间x(小时)的关系可近似地用二次函数y=ax?+bx表示;1.5
小时后(包括1.5
小时),y
与
x可近似地用反比例函数y=(k>0)表示,部分实验数据如表∶
时间
x(小时)
0.2
1
1.8
含药量
y(微克)
7.2
20
12.5
(1)求a、b及k的值;
(2)服药后几小时血液中的含药量达到最大值?最大值为多少?
(3)如果每毫升血液中含药量不少于10
微克时治疗疾病有效,那么成人按规定剂量服用该药一次后能维持多长的有效时间.(
≈1.41,精确到0.1
小时)
2020-2021学年度第一学期九年级数学质量检测试卷(三)
参考答案
(沪科版)
1-5.DDCDB
6-10.ACACD
11、(-2,-1)
12、16
13、15
14.10
原式
15、解:(1)
原式
16、解:∵在Rt△ABC中,∠C=90°,BC=6,AB=10,
∴AC=
∴
cosA
tanA
17、解:(1)设抛物线的解析式为y=-(x+1)(x-5),所以y=-x2+4x+5,
所以b=4,c=5;
(2)y=-x2+4x+5=-(x-2)2+9,P点坐标为(2,9),
所以△ABP的面积=×6×9=27
18【解答】解:(1)△A1B1C1如图所示,B1点的坐标为(1,-4);
(2)△A2B2C2如图所示,点B2的坐标为(-2,-1);
19【解答】(1)证明:∵DE∥AC,
∴∠DEB=∠FCE,
∴EF∥AB,∴∠DBE=∠FEC.
∴△BDEAEFC;
(2)解:∵EF∥AB.
∴
∵EC=BC-BE=12-B,
∴
解得:BE=4。
20、证明:(1)∵CD,BE分别是AB,AC边上的高,∴∠ADC=∠AEB=90°.
∵∠A=∠A,
∴△ACD∽△ABE
(2)连接DE,
∵△ACD∽△ABE,
∴AD:AE=AC:AB.
∴AD:AC=AE:AB.
∵∠A=∠A.
∴△AED∽△ABC
21.解:如图,过A作AE⊥CD垂足为E,设AE=x米,
在Rt△ABE中,tanB=,BE=,
在Rt△ABE中,tan∠ACD=
∴CE=
∵BC=BE-CE,
∴
解得:x=360。
答:小岛A到公路BD的距离为360米。
22.(1)证明:
∵AB⊥AC,AF⊥BE,
∴∠EAB=∠EFA=90°.
∵∠AEF=∠BEA
∴△AEF∽△BEA
∴
∴AE2=FE·BE
(2)解:∵E是AC的中点,
∴AE=CE,
∵AE2=FE·BE
∴CE2=FE·BE
∴
又∵∠CEF=∠BEC,
∴△CEF∽△BEC,
∴∠EFC=∠ECB.
∵AB=AC,∠BAC=90°,
∴∠ACB=45°
∴∠EFC=45°
∵∠AFE=90°
∴∠AFC=90°+45°=135°
23.解:(1)设1.5小时内,血液中含药量y(微克)与时间x(小时)的关系为y=ax2+bx,
根据表格得:
解得:a=-20,b=40,
1.5小时后(包括1.5小时),y与x可近似地用反比例函数y=(k>0),根据表格得:
k=1.8×12.5=22.5
∴a=-20
b=40
k=22.5;
(2)由(1)知y=-20x2+40x,
∵y=-20(x-1)2+20.
∴服药后1小时血液中的含药量达到最大值,最大值为20微克;
(3)当y=10时,10=-20x2+40x,或10=
解得:x=1-或x=1+(x>1.5,不合题意舍去),x=2.25
∴成人按规定剂量服用该药一次后能维持2.25-(1-)<2.0小时的有效时间
同课章节目录
