沪教版(上海)初中数学八年级第一学期:19.7 直角三角形全等的判定 教案
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期:19.7 直角三角形全等的判定 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 103.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览

文档简介
19.7直角三角形全等的判定
教学目标:
1、掌握直角三角形全等的判定定理,会判定直角三角形全等;
2、经历直角三角形全等判定定理“H.L”的探索过程,体会演绎思想和化归思想;
3、熟练掌握证明命题的一般步骤,正确画出命题的图形,写出已知、求证及证明.
教学重点:直角三角形全等的判定.
教学难点:三角形全等的判定方法和“H.L”
判定方法的灵活运用.
教学过程:
教师活动
学生活动
设计意图
一、
复习引入师:1.三角形全等的判定方法有哪几种?
2.三角形按角是怎样分类的?师:直角三角形是特殊的三角形,
除了全等三角形的四种判定方法来判定两个直角三角形全等以外,还有什么更为简单的判定两个直角三角形全等的方法?3.
对一般三角形而言,利用“边、边、角”不能判定两个三角形全等,它能否成为直角三角形全等的判定定理呢?
这节课我们将要研究这个问题.二、学习新知1、探究定理问1:两个直角三角形如果“边、边、角”对应相等,其中对应相等的角一定是直角,那么对应相等的边是哪两条?问2:斜边和一条直角边对应相等的两个直角三角形是否全等?你能把这个问题用命题的形式来表述吗?问3:怎样证明一个命题是真命题?已知:如图,在△ABC与△A'B'C'中,若AB=A'B',AC=A'C',∠C=∠C'=
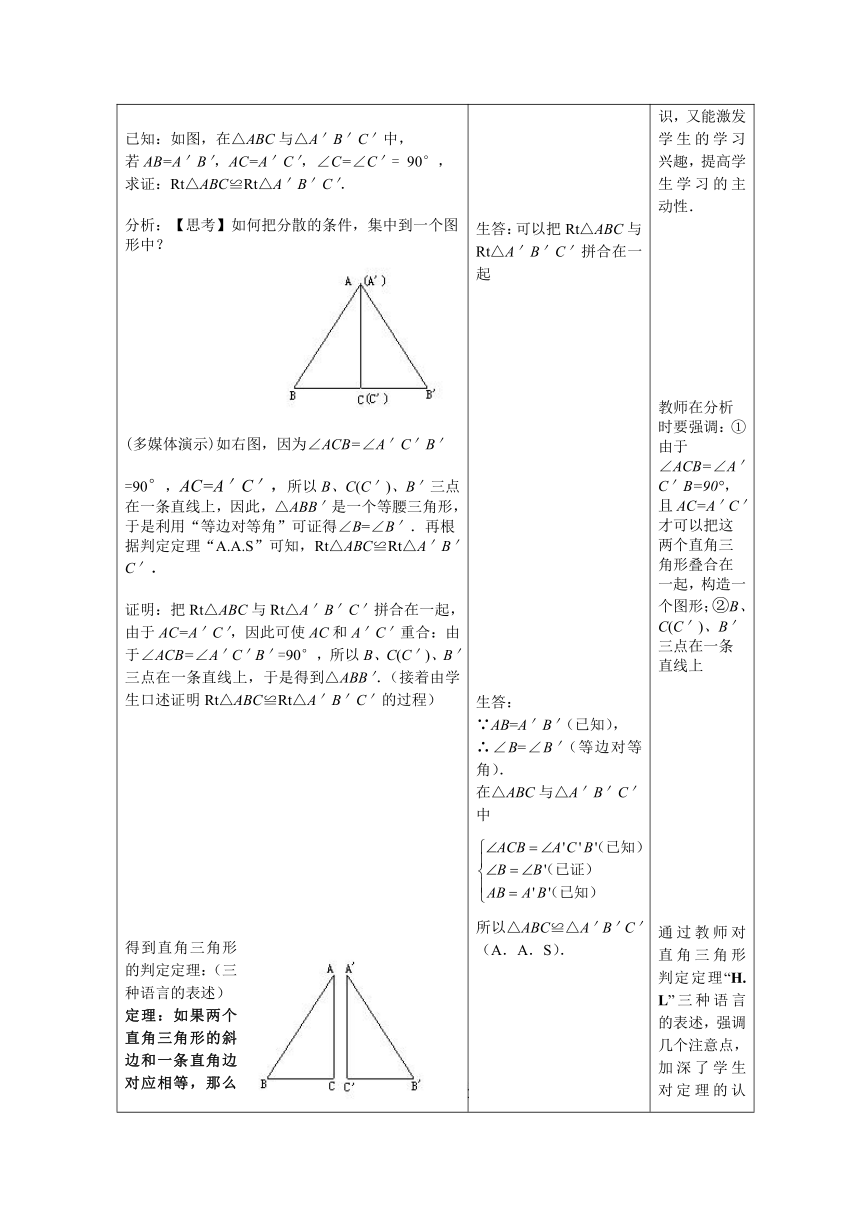
90°,求证:Rt△ABC≌Rt△A'B'C'.分析:【思考】如何把分散的条件,集中到一个图形中?
(多媒体演示)如右图,因为∠ACB=∠A'C'B'=90°,AC=A'C',所以B、C(C')、B'三点在一条直线上,因此,△ABB'是一个等腰三角形,于是利用“等边对等角”可证得∠B=∠B'.再根据判定定理“A.A.S”可知,Rt△ABC≌Rt△A'B'C'.证明:把Rt△ABC与Rt△A'B'C'拼合在一起,由于AC=A'C',因此可使AC和A'C'重合:由于∠ACB=∠A'C'B'=90°,所以B、C(C')、B'三点在一条直线上,于是得到△ABB'.(接着由学生口述证明Rt△ABC≌Rt△A'B'C'的过程)得到直角三角形的判定定理:(三种语言的表述)定理:如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等(简记为“H.
L”)
.在Rt△ABC和Rt△A'B'C'中,∴Rt△ABC
≌
Rt△A'B'C'(H.
L).归纳:应用判定定理“H.
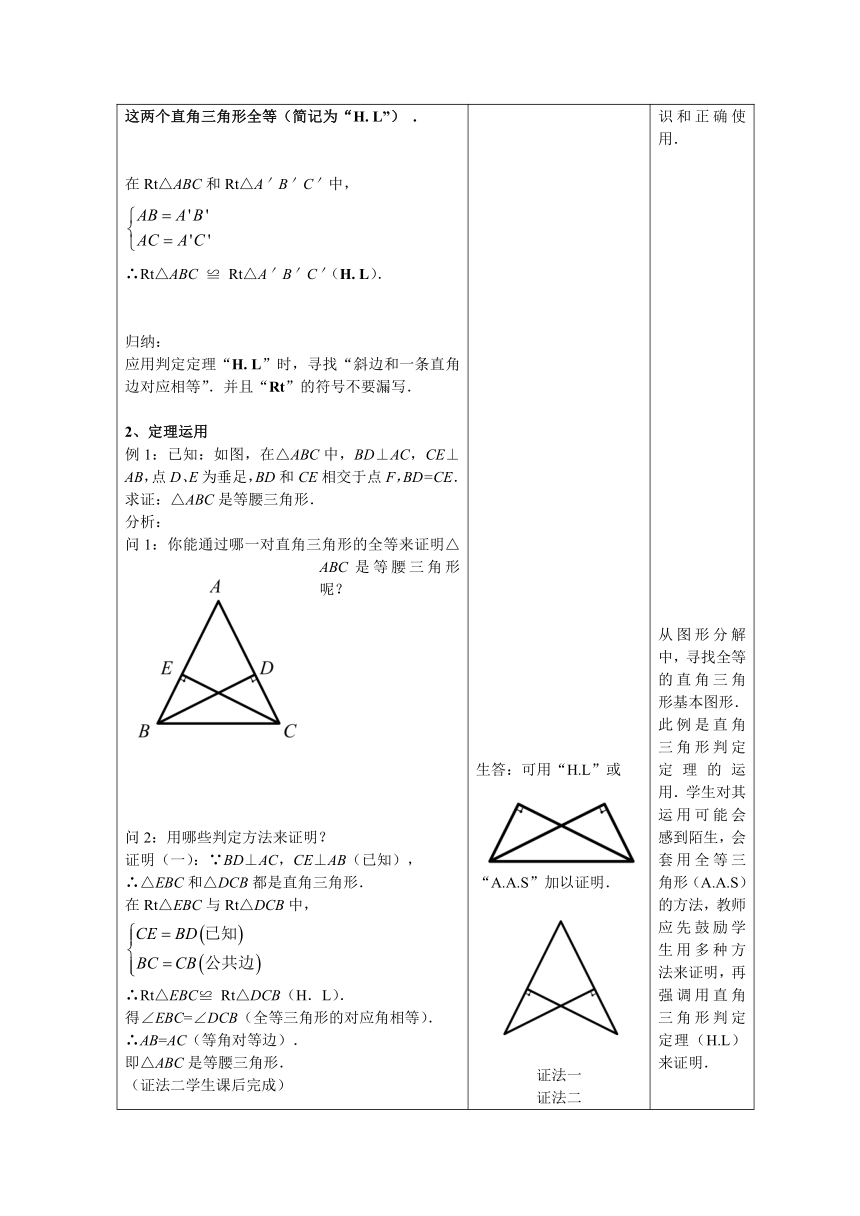
L”时,寻找“斜边和一条直角边对应相等”.并且“Rt”的符号不要漏写.2、定理运用例1:已知:如图,在△ABC中,BD⊥AC,CE⊥AB,点D、E为垂足,BD和CE相交于点F,BD=CE.求证:△ABC是等腰三角形.分析:问1:你能通过哪一对直角三角形的全等来证明△ABC是等腰三角形呢?问2:用哪些判定方法来证明?证明(一):∵BD⊥AC,CE⊥AB(已知),∴△EBC和△DCB都是直角三角形.在Rt△EBC与Rt△DCB中,∴Rt△EBC≌
Rt△DCB(H.L).得∠EBC=∠DCB(全等三角形的对应角相等).∴AB=AC(等角对等边).即△ABC是等腰三角形.(证法二学生课后完成)例2:求证:在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上.已知:如图,QD⊥OA,QE⊥OB,垂足分别是点D、E,且QD=QE.求证:点Q在∠AOB的平分线上.分析:问1:图中有Rt△吗?
追问:怎么办?证明:作射线OQ.∵QD⊥OA,QE⊥OB(已知),∴∠QDO=∠QEO=90°(垂直的定义).在Rt△QDO与Rt△QEO中,∴Rt△QDO≌Rt△QEO(H.L).得∠1=∠2(全等三角形的对应角相等).即OQ是∠AOB的平分线(角平分线的定义).∴点Q在∠AOB的平分线上.三、课堂反馈练习课本P114练习1:已知:如图,在△ABC中,AD是∠BAC的平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别为点E、F.求证:EB=FC教师点评:强调第1题用角平分线的性质定理证明DE=DF.练习4:已知:如图,AD⊥CD,BC⊥CD,D、C分别为垂足,AB的垂直平分线EF交AB于点E,交CD于点F,BC=DF.求证:AD=FC.第4题用线段垂直平分线的性质定理证明FA=FB.四、课堂小结通过本节课的学习你得到了哪些新知识,又有哪些收获?数学思想和方法:体现数学中所蕴涵的化归的思想.五、作业布置练习册
§19.7说明:课本中的练习课内完成不了的,可作为回家作业.
预设:生答:“S.A.S、A.S.A、A.A.S、S.S.S.”生答:锐角三角形、钝角三角形和直角三角形.生答:斜边和一条直角边生答:“如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等
.”生答:①根据题意画出图形,并在图上标出必要的字母或符号;②根据题设和结论,结合图形,写出“已知”和“求证”;③经过分析、找出由已知推出结论的途径,写出证明过程.生答:可以把Rt△ABC与Rt△A'B'C'拼合在一起生答:∵AB=A'B'(已知),∴∠B=∠B'(等边对等角).在△ABC与△A'B'C'中所以△ABC≌△A'B'C'(A.A.S).生答:可用“H.L”或“A.A.S”加以证明.证法一证法二预设:生答:没有?生答:添辅助线构建Rt△学生思考、分析并完成证明【练习1】证明:∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC
(已知),∴DE=DF
(在角平分线上的点到这个角的两边的距离相等).△BDE和△CDF都是直角三角形.在Rt△BDE和Rt△CDF中,∴Rt△BDE≌Rt△CDF(H.L).∴EB=FC(全等三角形的对应边相等).【练习4】证明:∵EF是AB的垂直平分线(已知),∴AF=BF(线段垂直平分线上的任意一点到这条线段两个端点的距离相等).∵AD⊥CD,BC⊥CD(已知),∴∠D=∠C=90°(垂直的定义).在Rt△ADF与Rt△FCB中,∴Rt△ADF≌Rt△FCB(H.L).∴AD=FC(全等三角形的对应边相等).生答:1.直角三角形全等的特殊的判定——“H.L”定理.2.运用“H.L”定理时,必须先得出两个直角三角形,然后依据斜边和一直角边对应相等,再证明两个直角三角形全等.
通过回忆,学生对全等三角形的判定定理和三角形按角的分类进行了复习,为引出新知作铺垫.复习、体验命题证明的步骤.学生通过思考,参与定理的验证过程,这样既进一步强化学生对定理的认识,又能激发学生的学习兴趣,提高学生学习的主动性.教师在分析时要强调:①由于∠ACB=∠A'C'B=90°,且AC=A'C'才可以把这两个直角三角形叠合在一起,构造一个图形;②B、C(C')、B'三点在一条直线上通过教师对直角三角形判定定理“H.
L”三种语言的表述,强调几个注意点,加深了学生对定理的认识和正确使用.从图形分解中,寻找全等的直角三角形基本图形.此例是直角三角形判定定理的运用.学生对其运用可能会感到陌生,会套用全等三角形(A.A.S)的方法,教师应先鼓励学生用多种方法来证明,再强调用直角三角形判定定理(H.L)来证明.本题是补证角的平分线性质定理的逆定理.在形式上,仍采用证明命题的方法,让学生再次体验证明命题的基本步骤.第1题是用角平分线的性质定理与直角三角形的判定定理“H.L”的综合运用;第4题是线段垂直平分线的性质定理与直角三角形的判定定理“H.L”的综合运用.所以选择这两题让学生练习,目的是培养学生综合运用知识的能力.
教学目标:
1、掌握直角三角形全等的判定定理,会判定直角三角形全等;
2、经历直角三角形全等判定定理“H.L”的探索过程,体会演绎思想和化归思想;
3、熟练掌握证明命题的一般步骤,正确画出命题的图形,写出已知、求证及证明.
教学重点:直角三角形全等的判定.
教学难点:三角形全等的判定方法和“H.L”
判定方法的灵活运用.
教学过程:
教师活动
学生活动
设计意图
一、
复习引入师:1.三角形全等的判定方法有哪几种?
2.三角形按角是怎样分类的?师:直角三角形是特殊的三角形,
除了全等三角形的四种判定方法来判定两个直角三角形全等以外,还有什么更为简单的判定两个直角三角形全等的方法?3.
对一般三角形而言,利用“边、边、角”不能判定两个三角形全等,它能否成为直角三角形全等的判定定理呢?
这节课我们将要研究这个问题.二、学习新知1、探究定理问1:两个直角三角形如果“边、边、角”对应相等,其中对应相等的角一定是直角,那么对应相等的边是哪两条?问2:斜边和一条直角边对应相等的两个直角三角形是否全等?你能把这个问题用命题的形式来表述吗?问3:怎样证明一个命题是真命题?已知:如图,在△ABC与△A'B'C'中,若AB=A'B',AC=A'C',∠C=∠C'=
90°,求证:Rt△ABC≌Rt△A'B'C'.分析:【思考】如何把分散的条件,集中到一个图形中?
(多媒体演示)如右图,因为∠ACB=∠A'C'B'=90°,AC=A'C',所以B、C(C')、B'三点在一条直线上,因此,△ABB'是一个等腰三角形,于是利用“等边对等角”可证得∠B=∠B'.再根据判定定理“A.A.S”可知,Rt△ABC≌Rt△A'B'C'.证明:把Rt△ABC与Rt△A'B'C'拼合在一起,由于AC=A'C',因此可使AC和A'C'重合:由于∠ACB=∠A'C'B'=90°,所以B、C(C')、B'三点在一条直线上,于是得到△ABB'.(接着由学生口述证明Rt△ABC≌Rt△A'B'C'的过程)得到直角三角形的判定定理:(三种语言的表述)定理:如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等(简记为“H.
L”)
.在Rt△ABC和Rt△A'B'C'中,∴Rt△ABC
≌
Rt△A'B'C'(H.
L).归纳:应用判定定理“H.
L”时,寻找“斜边和一条直角边对应相等”.并且“Rt”的符号不要漏写.2、定理运用例1:已知:如图,在△ABC中,BD⊥AC,CE⊥AB,点D、E为垂足,BD和CE相交于点F,BD=CE.求证:△ABC是等腰三角形.分析:问1:你能通过哪一对直角三角形的全等来证明△ABC是等腰三角形呢?问2:用哪些判定方法来证明?证明(一):∵BD⊥AC,CE⊥AB(已知),∴△EBC和△DCB都是直角三角形.在Rt△EBC与Rt△DCB中,∴Rt△EBC≌
Rt△DCB(H.L).得∠EBC=∠DCB(全等三角形的对应角相等).∴AB=AC(等角对等边).即△ABC是等腰三角形.(证法二学生课后完成)例2:求证:在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上.已知:如图,QD⊥OA,QE⊥OB,垂足分别是点D、E,且QD=QE.求证:点Q在∠AOB的平分线上.分析:问1:图中有Rt△吗?
追问:怎么办?证明:作射线OQ.∵QD⊥OA,QE⊥OB(已知),∴∠QDO=∠QEO=90°(垂直的定义).在Rt△QDO与Rt△QEO中,∴Rt△QDO≌Rt△QEO(H.L).得∠1=∠2(全等三角形的对应角相等).即OQ是∠AOB的平分线(角平分线的定义).∴点Q在∠AOB的平分线上.三、课堂反馈练习课本P114练习1:已知:如图,在△ABC中,AD是∠BAC的平分线,且BD=CD,DE、DF分别垂直于AB、AC,垂足分别为点E、F.求证:EB=FC教师点评:强调第1题用角平分线的性质定理证明DE=DF.练习4:已知:如图,AD⊥CD,BC⊥CD,D、C分别为垂足,AB的垂直平分线EF交AB于点E,交CD于点F,BC=DF.求证:AD=FC.第4题用线段垂直平分线的性质定理证明FA=FB.四、课堂小结通过本节课的学习你得到了哪些新知识,又有哪些收获?数学思想和方法:体现数学中所蕴涵的化归的思想.五、作业布置练习册
§19.7说明:课本中的练习课内完成不了的,可作为回家作业.
预设:生答:“S.A.S、A.S.A、A.A.S、S.S.S.”生答:锐角三角形、钝角三角形和直角三角形.生答:斜边和一条直角边生答:“如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等
.”生答:①根据题意画出图形,并在图上标出必要的字母或符号;②根据题设和结论,结合图形,写出“已知”和“求证”;③经过分析、找出由已知推出结论的途径,写出证明过程.生答:可以把Rt△ABC与Rt△A'B'C'拼合在一起生答:∵AB=A'B'(已知),∴∠B=∠B'(等边对等角).在△ABC与△A'B'C'中所以△ABC≌△A'B'C'(A.A.S).生答:可用“H.L”或“A.A.S”加以证明.证法一证法二预设:生答:没有?生答:添辅助线构建Rt△学生思考、分析并完成证明【练习1】证明:∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC
(已知),∴DE=DF
(在角平分线上的点到这个角的两边的距离相等).△BDE和△CDF都是直角三角形.在Rt△BDE和Rt△CDF中,∴Rt△BDE≌Rt△CDF(H.L).∴EB=FC(全等三角形的对应边相等).【练习4】证明:∵EF是AB的垂直平分线(已知),∴AF=BF(线段垂直平分线上的任意一点到这条线段两个端点的距离相等).∵AD⊥CD,BC⊥CD(已知),∴∠D=∠C=90°(垂直的定义).在Rt△ADF与Rt△FCB中,∴Rt△ADF≌Rt△FCB(H.L).∴AD=FC(全等三角形的对应边相等).生答:1.直角三角形全等的特殊的判定——“H.L”定理.2.运用“H.L”定理时,必须先得出两个直角三角形,然后依据斜边和一直角边对应相等,再证明两个直角三角形全等.
通过回忆,学生对全等三角形的判定定理和三角形按角的分类进行了复习,为引出新知作铺垫.复习、体验命题证明的步骤.学生通过思考,参与定理的验证过程,这样既进一步强化学生对定理的认识,又能激发学生的学习兴趣,提高学生学习的主动性.教师在分析时要强调:①由于∠ACB=∠A'C'B=90°,且AC=A'C'才可以把这两个直角三角形叠合在一起,构造一个图形;②B、C(C')、B'三点在一条直线上通过教师对直角三角形判定定理“H.
L”三种语言的表述,强调几个注意点,加深了学生对定理的认识和正确使用.从图形分解中,寻找全等的直角三角形基本图形.此例是直角三角形判定定理的运用.学生对其运用可能会感到陌生,会套用全等三角形(A.A.S)的方法,教师应先鼓励学生用多种方法来证明,再强调用直角三角形判定定理(H.L)来证明.本题是补证角的平分线性质定理的逆定理.在形式上,仍采用证明命题的方法,让学生再次体验证明命题的基本步骤.第1题是用角平分线的性质定理与直角三角形的判定定理“H.L”的综合运用;第4题是线段垂直平分线的性质定理与直角三角形的判定定理“H.L”的综合运用.所以选择这两题让学生练习,目的是培养学生综合运用知识的能力.
