四川省眉山市彭山区第一中学2020-2021学年高一12月月考数学试卷 Word版无答案
文档属性
| 名称 | 四川省眉山市彭山区第一中学2020-2021学年高一12月月考数学试卷 Word版无答案 |  | |
| 格式 | zip | ||
| 文件大小 | 192.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 19:50:53 | ||
图片预览

文档简介
彭山一中2023届高一上期12月月考
数学试卷(12.8-9)
选择题(共12×5=60分)
1.已知集合M={x∈Z
|
0<x<6},N={x|x>3},P=M∩N,则P的子集共有(
)
A.1个
B.2个
C.4个
D.8个
2.函数(,且)的图象一定经过的点是(
)
A.
B.
C.
D.
3.函数y的定义域是(
)
A.(﹣1,+∞)
B.(﹣1,0)∪(0,+∞)
C.[﹣1,+∞)
D.[﹣2,0)∪(0,+∞)
4.下列大小关系正确的是(
)
A.
B.
C.
D.
5.幂函数f
(x)的图象过点,则f
(x)的一个单调递减区间是(
)
A.(0,+∞)
B.[0,+∞)
C.(﹣∞,0]
D.(﹣∞,0)
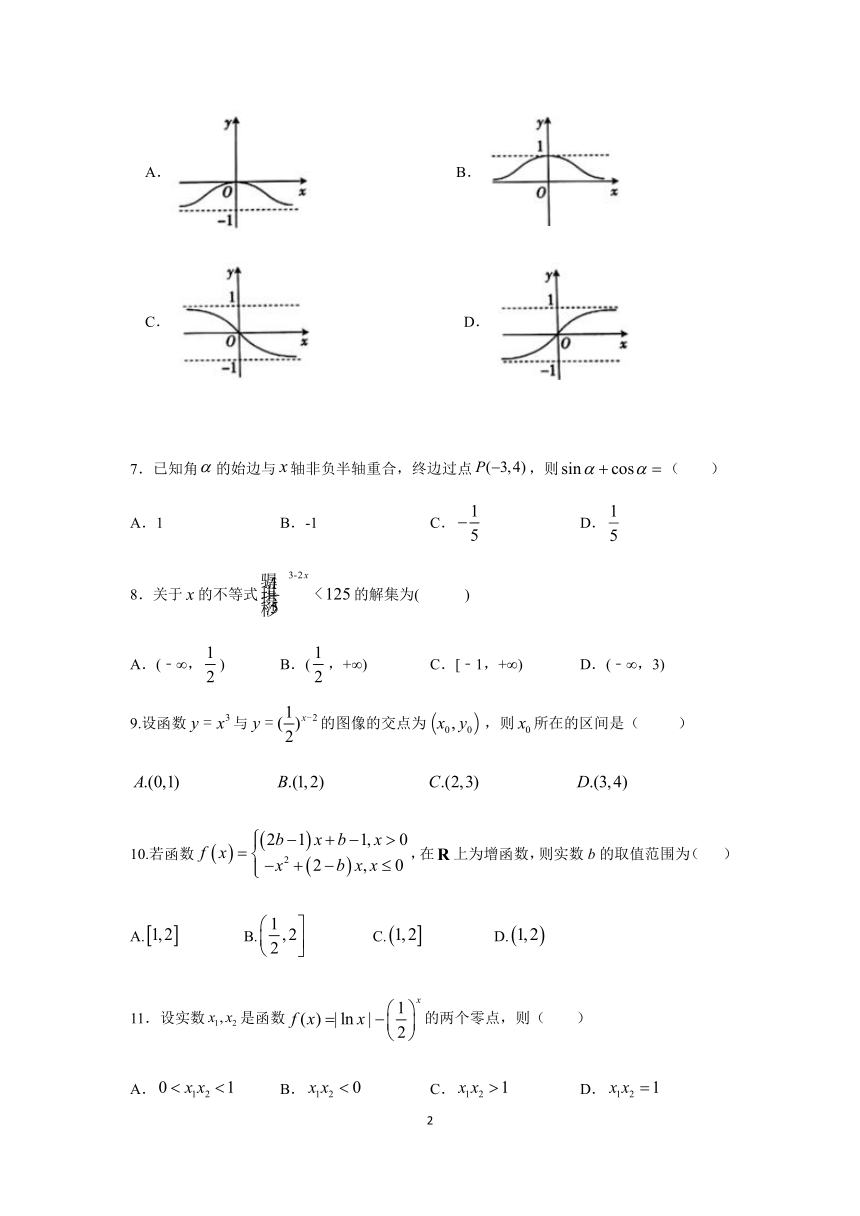
6.函数的图象大致是(
)
A.
B.
C.
D.
7.已知角的始边与轴非负半轴重合,终边过点,则(
)
A.1
B.-1
C.
D.
8.关于的不等式的解集为(
)
A.(﹣∞,)
B.(,+∞)
C.[﹣1,+∞)
D.(﹣∞,3)
9.设函数与的图像的交点为,则所在的区间是(
)
10.若函数,在上为增函数,则实数b的取值范围为(
)
A.
B.
C.
D.
11.设实数是函数的两个零点,则(
)
A.
B.
C.
D.
12.设函数,若关于的方程有四个不同的解,且,则的取值范围是(
)
A.
B.
C.
D.
填空题(共4×5=20分)
已知,则=______________.
设,则______________.
函数的单调减区间为______________.
16.已知函数满足,对任意的都有恒成立,且,则关于的不等式的解集为________.
解答题(共6题,70分)
(10分)
计算:
已知,的值;
(2)
.
(12分)
已知,.
(1)求;(2)若,若,求m的取值范围.
(12分)
已知函数是定义在上的奇函数,当时有.
(1)求函数的解析式;
(2)判断函数在上的单调性,并用定义证明.
(12分)
已知二次函数满足以下要求:①函数的值域为;②对恒成立。
求:(1)求函数的解析式;
(2)设,求时的值域。
21.(12分)
某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数与听课时间(单位:分钟)之间的关系满足如图所示的曲线.当时,曲线是二次函数图象的一部分,当时,曲线是函数图象的一部分.根据专家研究,当注意力指数大于80时学习效果最佳.
(1)试求的函数关系式;
(2)教师在什么时段内安排核心内容,能使得学生学习效果最佳?请说明理由.
22.(12分)
已知函数f(x)=x2﹣2x+1+a在区间[1,2]上有最小值﹣1.
(1)求实数a的值;
(2)若关于x的方程f(log2x)+1﹣2klog2x=0在[2,4]上有解,求实数k的取值范围;
(3)若对任意的x1,x2∈(1,2],任意的p∈[﹣1,1],都有
|f(x1)﹣f(x2)|≤m2﹣2mp﹣2成立,求实数m的取值范围.
(附:函数g(t)=t在(0,1)单调递减,在(1,+∞)单调递增.)
数学试卷(12.8-9)
选择题(共12×5=60分)
1.已知集合M={x∈Z
|
0<x<6},N={x|x>3},P=M∩N,则P的子集共有(
)
A.1个
B.2个
C.4个
D.8个
2.函数(,且)的图象一定经过的点是(
)
A.
B.
C.
D.
3.函数y的定义域是(
)
A.(﹣1,+∞)
B.(﹣1,0)∪(0,+∞)
C.[﹣1,+∞)
D.[﹣2,0)∪(0,+∞)
4.下列大小关系正确的是(
)
A.
B.
C.
D.
5.幂函数f
(x)的图象过点,则f
(x)的一个单调递减区间是(
)
A.(0,+∞)
B.[0,+∞)
C.(﹣∞,0]
D.(﹣∞,0)
6.函数的图象大致是(
)
A.
B.
C.
D.
7.已知角的始边与轴非负半轴重合,终边过点,则(
)
A.1
B.-1
C.
D.
8.关于的不等式的解集为(
)
A.(﹣∞,)
B.(,+∞)
C.[﹣1,+∞)
D.(﹣∞,3)
9.设函数与的图像的交点为,则所在的区间是(
)
10.若函数,在上为增函数,则实数b的取值范围为(
)
A.
B.
C.
D.
11.设实数是函数的两个零点,则(
)
A.
B.
C.
D.
12.设函数,若关于的方程有四个不同的解,且,则的取值范围是(
)
A.
B.
C.
D.
填空题(共4×5=20分)
已知,则=______________.
设,则______________.
函数的单调减区间为______________.
16.已知函数满足,对任意的都有恒成立,且,则关于的不等式的解集为________.
解答题(共6题,70分)
(10分)
计算:
已知,的值;
(2)
.
(12分)
已知,.
(1)求;(2)若,若,求m的取值范围.
(12分)
已知函数是定义在上的奇函数,当时有.
(1)求函数的解析式;
(2)判断函数在上的单调性,并用定义证明.
(12分)
已知二次函数满足以下要求:①函数的值域为;②对恒成立。
求:(1)求函数的解析式;
(2)设,求时的值域。
21.(12分)
某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数与听课时间(单位:分钟)之间的关系满足如图所示的曲线.当时,曲线是二次函数图象的一部分,当时,曲线是函数图象的一部分.根据专家研究,当注意力指数大于80时学习效果最佳.
(1)试求的函数关系式;
(2)教师在什么时段内安排核心内容,能使得学生学习效果最佳?请说明理由.
22.(12分)
已知函数f(x)=x2﹣2x+1+a在区间[1,2]上有最小值﹣1.
(1)求实数a的值;
(2)若关于x的方程f(log2x)+1﹣2klog2x=0在[2,4]上有解,求实数k的取值范围;
(3)若对任意的x1,x2∈(1,2],任意的p∈[﹣1,1],都有
|f(x1)﹣f(x2)|≤m2﹣2mp﹣2成立,求实数m的取值范围.
(附:函数g(t)=t在(0,1)单调递减,在(1,+∞)单调递增.)
同课章节目录
