12.2.4直角三角形全等的判定-人教版八年级数学上册导学案(含答案)
文档属性
| 名称 | 12.2.4直角三角形全等的判定-人教版八年级数学上册导学案(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 750.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览

文档简介
12.2.4直角三角形全等的判定
备课时间: 授课时间: 年班:
学习目标:
1、知识与技能:掌握直角三角形全等的条件,并能运用其解决一些实际问题。
2、过程与方法:经历探索直角三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程。
3、情感态度与价值观:在学习过程中,通过交流合作,使学生体会成功的喜悦。
学习重点:运用直角三角形全等的条件解决一些实际问题。
学习难点:熟练运用直角三角形全等的条件解决一些实际问题。
学习过程:
一、自主学习:
1、复习思考:
(1)、判定两个三角形全等的方法: 、 、 、
(2)、如图,Rt△ABC中,直角边是 、 ,斜边是
(3)、如图,AB⊥BE于B,DE⊥BE于E,
①若∠A=∠D,AB=DE,则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
②若∠A=∠D,BC=EF,则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
③若AB=DE,BC=EF,则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
④若AB=DE,BC=EF,AC=DF,则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
2、如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
(1)动手试一试。
已知:Rt△ABC 求作:Rt△, 使=90°, =AB, =BC
作法:
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
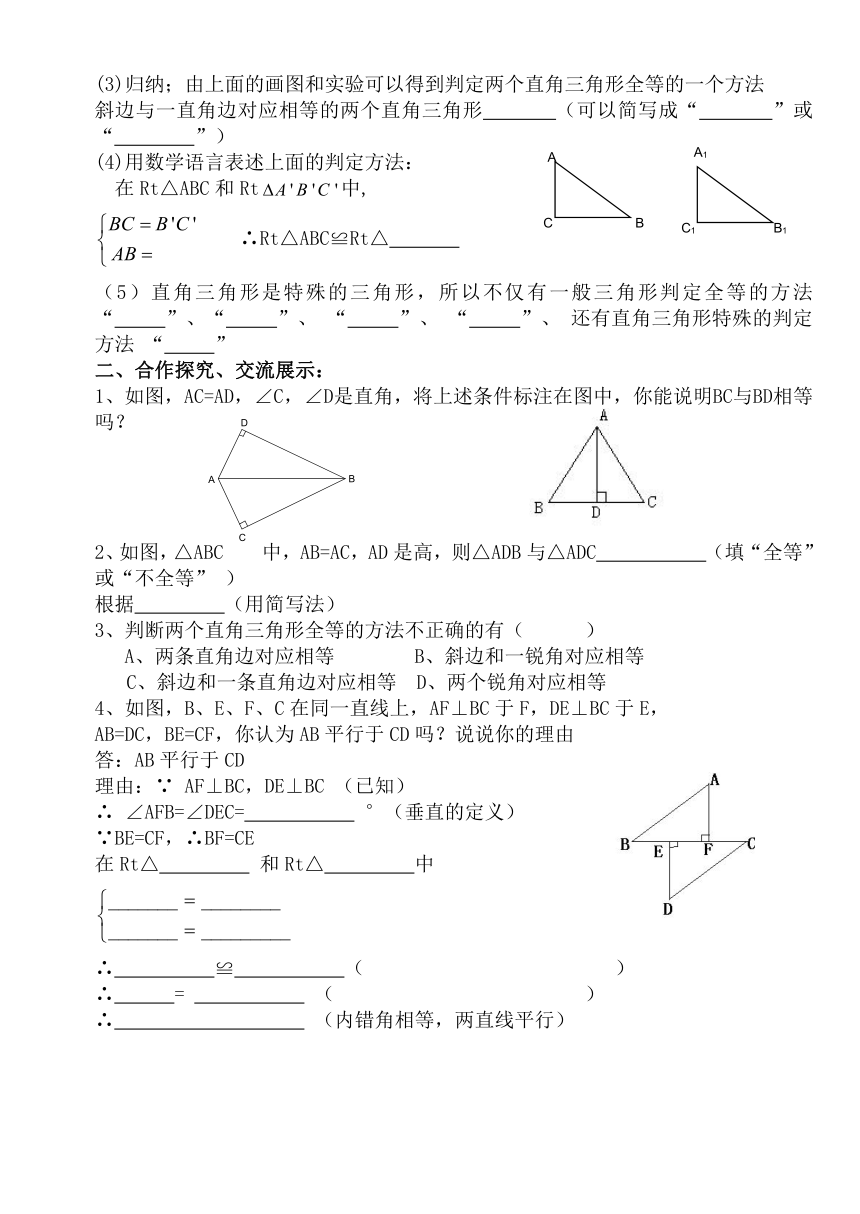
(3)归纳;由上面的画图和实验可以得到判定两个直角三角形全等的一个方法
斜边与一直角边对应相等的两个直角三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述上面的判定方法:
在Rt△ABC和Rt中,
∴Rt△ABC≌Rt△
(5)直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法 “ ”、“ ”、 “ ”、 “ ”、 还有直角三角形特殊的判定方法 “ ”
二、合作探究、交流展示:
1、如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
2、如图,△ABC中,AB=AC,AD是高,则△ADB与△ADC (填“全等”或“不全等” )
根据 (用简写法)
3、判断两个直角三角形全等的方法不正确的有( )
A、两条直角边对应相等 B、斜边和一锐角对应相等
C、斜边和一条直角边对应相等 D、两个锐角对应相等
4、如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,
AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由
答:AB平行于CD
理由:∵ AF⊥BC,DE⊥BC (已知)
∴ ∠AFB=∠DEC= °(垂直的定义)
∵BE=CF,∴BF=CE
在Rt△ 和Rt△ 中
∴ ≌ ( )
∴ = ( )
∴ (内错角相等,两直线平行)
三、拓展延伸:
如图1,E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点。(1)求证:MB=MD,ME=MF;(2)当E、F两点移动至图2所示的位置时,其余条件不变,上述结论是否成立?若成立,给予证明。
四、课堂检测:
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据
(4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,根据
(5)若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据
五、学(教)后反思 :
答案
一、自主学习:
1、(1)SSS SAS AAS ASA
(2)AC BC AB
(3)①全等;ASA
②全等;AAS
③全等;SAS
④全等;SSS
2、(1)(2) 略
(3)全等;斜边、直角边;HL
(4)A’B’;
(5)SSS SAS AAS ASA HL
二、合作探究、交流展示:
1、解:∵∠C、∠D是直角
∴△ABC和△ABD都是直角三角形
在Rt△ABC和Rt△ABD中
∴Rt△ABC≌Rt△ABD(HL)
∴BC=BD
2、全等;HL
3、D
4、90°;ABF;DCE;BF;CE;AB;DC;Rt△ABF;Rt△DCE;HL;∠B;∠C;全等三角形对应角相等;AB∥CD
三、拓展延伸:
解答:
(1)证明:∵DE⊥AC,BF⊥AC,
∴∠AFB=90°,∠DEC=90°,
在Rt△ABF和Rt△CDE中,
∴Rt△ABF≌Rt△CDE,
∴BF=DE.
在△BFM和△DEM中,?
????
∴△BFM≌△DEM,
∴MB=MD,ME=MF;
(2)上述结论成立,仍存在MB=MD,ME=MF.
理由如下:
∵DE⊥AC,BF⊥AC
∴∠AFB=∠BFM=∠DEC=∠DEM=90°,
在Rt△ABF和Rt△CDE中,
∴Rt△ABF≌Rt△CDE,
∴BF=DE.
在△BFM和△DEM中,
?????
∴△BFM≌△DEM,
∴MB=MD,ME=MF.
四、课堂检测:
(1)AAS
(2)ASA
(3)SAS
(4)SSS
(5)HL
备课时间: 授课时间: 年班:
学习目标:
1、知识与技能:掌握直角三角形全等的条件,并能运用其解决一些实际问题。
2、过程与方法:经历探索直角三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程。
3、情感态度与价值观:在学习过程中,通过交流合作,使学生体会成功的喜悦。
学习重点:运用直角三角形全等的条件解决一些实际问题。
学习难点:熟练运用直角三角形全等的条件解决一些实际问题。
学习过程:
一、自主学习:
1、复习思考:
(1)、判定两个三角形全等的方法: 、 、 、
(2)、如图,Rt△ABC中,直角边是 、 ,斜边是
(3)、如图,AB⊥BE于B,DE⊥BE于E,
①若∠A=∠D,AB=DE,则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
②若∠A=∠D,BC=EF,则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
③若AB=DE,BC=EF,则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
④若AB=DE,BC=EF,AC=DF,则△ABC与△DEF (填“全等”或“不全等” )根据 (用简写法)
2、如果两个直角三角形满足斜边和一条直角边对应相等,这两个直角三角形全等吗?
(1)动手试一试。
已知:Rt△ABC 求作:Rt△, 使=90°, =AB, =BC
作法:
(2) 把△剪下来放到△ABC上,观察△与△ABC是否能够完全重合?
(3)归纳;由上面的画图和实验可以得到判定两个直角三角形全等的一个方法
斜边与一直角边对应相等的两个直角三角形 (可以简写成“ ”或“ ”)
(4)用数学语言表述上面的判定方法:
在Rt△ABC和Rt中,
∴Rt△ABC≌Rt△
(5)直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法 “ ”、“ ”、 “ ”、 “ ”、 还有直角三角形特殊的判定方法 “ ”
二、合作探究、交流展示:
1、如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?
2、如图,△ABC中,AB=AC,AD是高,则△ADB与△ADC (填“全等”或“不全等” )
根据 (用简写法)
3、判断两个直角三角形全等的方法不正确的有( )
A、两条直角边对应相等 B、斜边和一锐角对应相等
C、斜边和一条直角边对应相等 D、两个锐角对应相等
4、如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,
AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由
答:AB平行于CD
理由:∵ AF⊥BC,DE⊥BC (已知)
∴ ∠AFB=∠DEC= °(垂直的定义)
∵BE=CF,∴BF=CE
在Rt△ 和Rt△ 中
∴ ≌ ( )
∴ = ( )
∴ (内错角相等,两直线平行)
三、拓展延伸:
如图1,E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF=CE,BD交AC于M点。(1)求证:MB=MD,ME=MF;(2)当E、F两点移动至图2所示的位置时,其余条件不变,上述结论是否成立?若成立,给予证明。
四、课堂检测:
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,根据
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,根据
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,根据
(4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,根据
(5)若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,根据
五、学(教)后反思 :
答案
一、自主学习:
1、(1)SSS SAS AAS ASA
(2)AC BC AB
(3)①全等;ASA
②全等;AAS
③全等;SAS
④全等;SSS
2、(1)(2) 略
(3)全等;斜边、直角边;HL
(4)A’B’;
(5)SSS SAS AAS ASA HL
二、合作探究、交流展示:
1、解:∵∠C、∠D是直角
∴△ABC和△ABD都是直角三角形
在Rt△ABC和Rt△ABD中
∴Rt△ABC≌Rt△ABD(HL)
∴BC=BD
2、全等;HL
3、D
4、90°;ABF;DCE;BF;CE;AB;DC;Rt△ABF;Rt△DCE;HL;∠B;∠C;全等三角形对应角相等;AB∥CD
三、拓展延伸:
解答:
(1)证明:∵DE⊥AC,BF⊥AC,
∴∠AFB=90°,∠DEC=90°,
在Rt△ABF和Rt△CDE中,
∴Rt△ABF≌Rt△CDE,
∴BF=DE.
在△BFM和△DEM中,?
????
∴△BFM≌△DEM,
∴MB=MD,ME=MF;
(2)上述结论成立,仍存在MB=MD,ME=MF.
理由如下:
∵DE⊥AC,BF⊥AC
∴∠AFB=∠BFM=∠DEC=∠DEM=90°,
在Rt△ABF和Rt△CDE中,
∴Rt△ABF≌Rt△CDE,
∴BF=DE.
在△BFM和△DEM中,
?????
∴△BFM≌△DEM,
∴MB=MD,ME=MF.
四、课堂检测:
(1)AAS
(2)ASA
(3)SAS
(4)SSS
(5)HL
