人教版八年级上册 12.2全等三角形的判定2(共19张ppt)
文档属性
| 名称 | 人教版八年级上册 12.2全等三角形的判定2(共19张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 319.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 09:42:46 | ||
图片预览


文档简介
(共19张PPT)
12.2
三角形全等的判定
(第2课时)
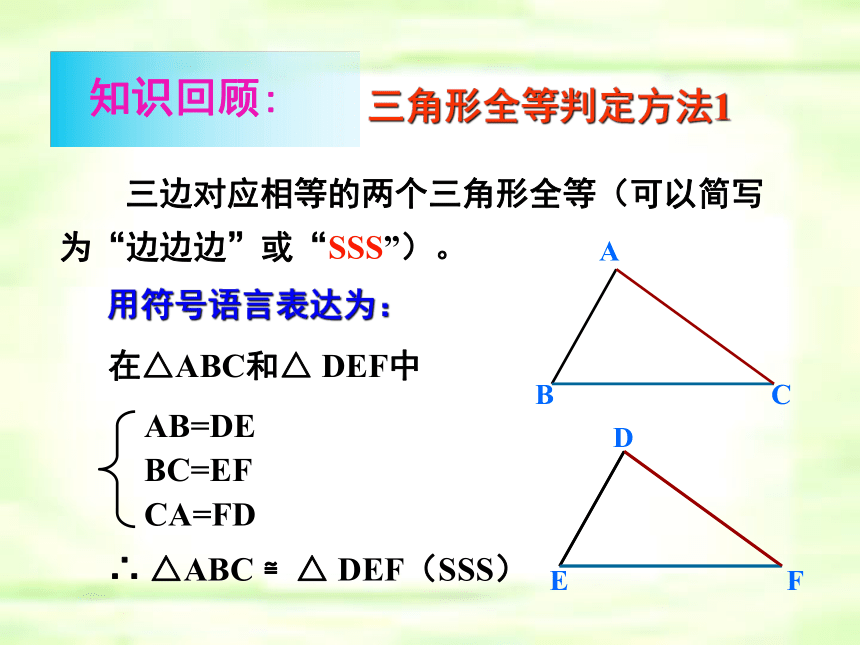
三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。
A
B
C
D
E
F
在△ABC和△
DEF中
∴
△ABC
≌△
DEF(SSS)
AB=DE
BC=EF
CA=FD
用符号语言表达为:
三角形全等判定方法1
知识回顾:
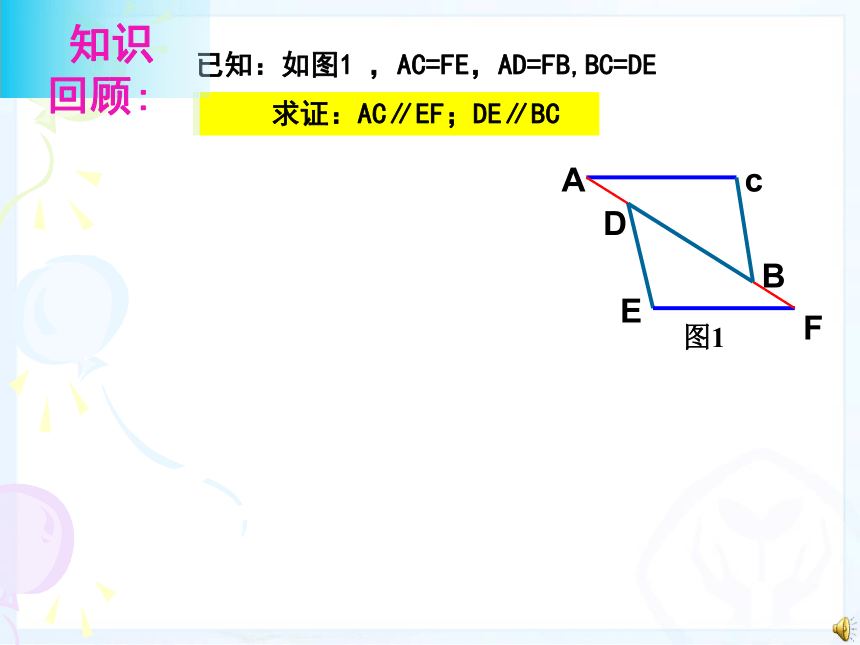
图1
已知:如图1
,AC=FE,AD=FB,BC=DE
求证:△ABC≌△FDE
求证:∠C=∠E
,
A
c
E
D
B
F
求证:AC∥EF;DE∥BC
知识
回顾:
除了SSS外,还有其他情况吗?继续探索三角形全等的条件.
思考
(2)
三条边
(1)
三个角
(3)
两边一角
(4)
两角一边
当两个三角形满足六个条件中的三个时,有四种情况:
SSS
不能!
?
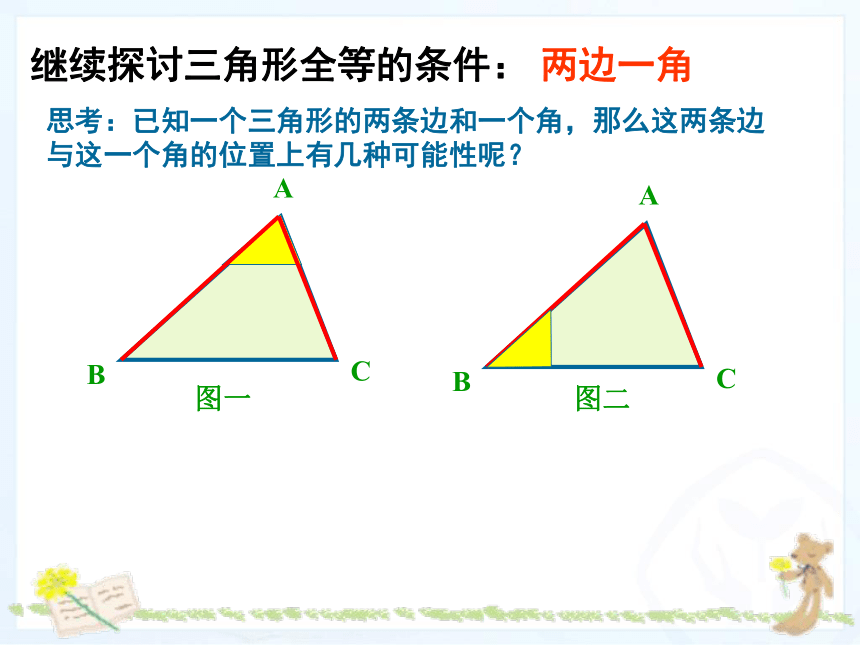
继续探讨三角形全等的条件:
两边一角
思考:已知一个三角形的两条边和一个角,那么这两条边
与这一个角的位置上有几种可能性呢?
A
B
C
A
B
C
图一
图二
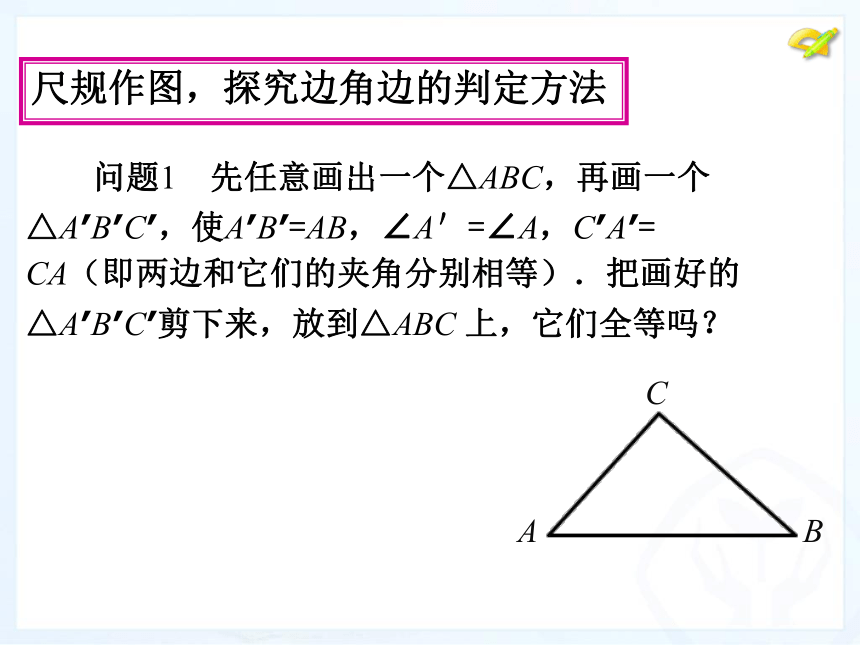
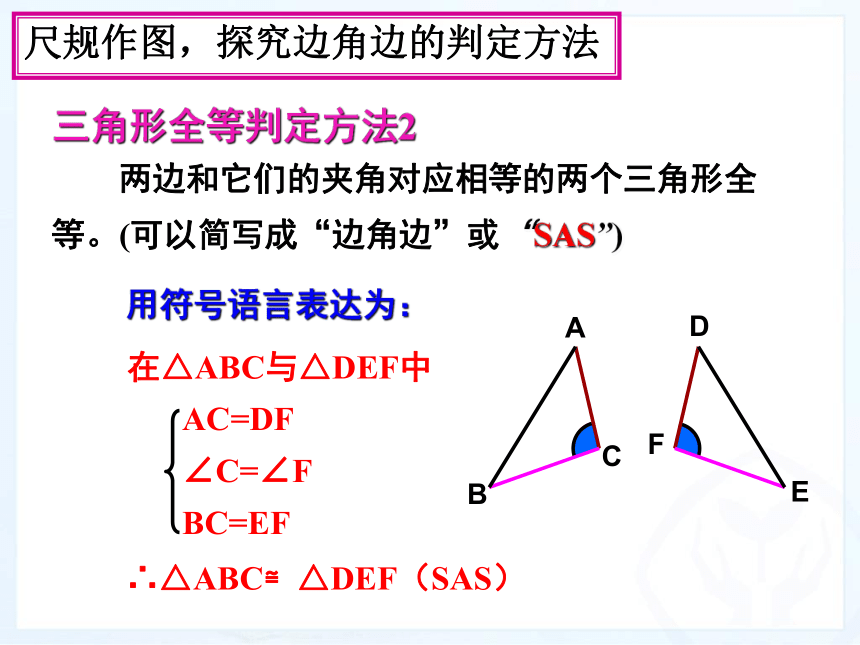
尺规作图,探究边角边的判定方法
问题1 先任意画出一个△ABC,再画一个
△A′B′C′,使A′B′=AB,∠A'=∠A,C′A′=
CA(即两边和它们的夹角分别相等).把画好的
△A′B′C′剪下来,放到△ABC
上,它们全等吗?
A
B
C
三角形全等判定方法2
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS)
两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
F
E
D
C
B
A
AC=DF
∠C=∠F
BC=EF
尺规作图,探究边角边的判定方法
例1
已知:
如图,AC=AD
,∠CAB=∠DAB.
求证:
△ACB
≌
△ADB.
A
B
C
D
证明:
在△ACB
和
△ADB中
AC
=
A
D
∠CAB=∠DAB
A
B
=
A
B
(公共边)
∴△ACB≌△ADB
(SAS)
课堂练习
证明三角形全等的步骤:
?1.写出在哪两个三角形中证明全等。(注意把表示对应顶点的字母写在对应的位置上).
?2.按边、角、边的顺序列出三个条件,用大括号合在一起.
?3.写出结论.每步要有推理的依据.
已知:如图,MA=NB,MC=ND,∠M=∠N.
求证:AB=CD.
课堂练习
F
A
B
D
C
E
点E、F在AC上,AD//BC,AD=CB,AE=CF
求证:△AFD≌△CEB
课堂练习
综合提高
已知:AB=AD,CB=CD.
求证:AC⊥BD.
如右图,
如图,在△ABC
和△ABD
中,
AB
=AB,AC
=
AD,∠B
=∠B,
但△ABC
和△ABD
不全等.
探索“SSA”能否识别两三角形全等
问题3
两边一角分别相等包括“两边夹角”和
“两边及其中一边的对角”分别相等两种情况,前面已
探索出“SAS”判定三角形全等的方法,那么由“SSA”
的条件能判定两个三角形全等吗?
A
B
C
D
三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。
A
B
C
D
E
F
在△ABC和△
DEF中
∴
△ABC
≌△
DEF(SSS)
AB=DE
BC=EF
CA=FD
用符号语言表达为:
三角形全等判定方法1
知识梳理:
三角形全等判定方法2
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS)
两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
知识梳理:
F
E
D
C
B
A
AC=DF
∠C=∠F
BC=EF
知识梳理:
A
B
D
A
B
C
SSA不能判定全等
课堂练习
1、已知:如图,AB=AD,AC=AE,∠1=∠2.
求证:△ABC≌△ADE.
1
2
2、已知:如图,点A、B、C、D在同一条直线上,AC=DB,AE=DF,EA⊥AD,FD⊥AD,垂足分别是A,D。
求证:△EAB≌△FDC
A
E
B
C
D
F
3、已知:如图,AB=AC,AD=AE,∠1=∠2,
求证:△ABD≌△ACE
A
C
B
E
D
12.2
三角形全等的判定
(第2课时)
三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。
A
B
C
D
E
F
在△ABC和△
DEF中
∴
△ABC
≌△
DEF(SSS)
AB=DE
BC=EF
CA=FD
用符号语言表达为:
三角形全等判定方法1
知识回顾:
图1
已知:如图1
,AC=FE,AD=FB,BC=DE
求证:△ABC≌△FDE
求证:∠C=∠E
,
A
c
E
D
B
F
求证:AC∥EF;DE∥BC
知识
回顾:
除了SSS外,还有其他情况吗?继续探索三角形全等的条件.
思考
(2)
三条边
(1)
三个角
(3)
两边一角
(4)
两角一边
当两个三角形满足六个条件中的三个时,有四种情况:
SSS
不能!
?
继续探讨三角形全等的条件:
两边一角
思考:已知一个三角形的两条边和一个角,那么这两条边
与这一个角的位置上有几种可能性呢?
A
B
C
A
B
C
图一
图二
尺规作图,探究边角边的判定方法
问题1 先任意画出一个△ABC,再画一个
△A′B′C′,使A′B′=AB,∠A'=∠A,C′A′=
CA(即两边和它们的夹角分别相等).把画好的
△A′B′C′剪下来,放到△ABC
上,它们全等吗?
A
B
C
三角形全等判定方法2
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS)
两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
F
E
D
C
B
A
AC=DF
∠C=∠F
BC=EF
尺规作图,探究边角边的判定方法
例1
已知:
如图,AC=AD
,∠CAB=∠DAB.
求证:
△ACB
≌
△ADB.
A
B
C
D
证明:
在△ACB
和
△ADB中
AC
=
A
D
∠CAB=∠DAB
A
B
=
A
B
(公共边)
∴△ACB≌△ADB
(SAS)
课堂练习
证明三角形全等的步骤:
?1.写出在哪两个三角形中证明全等。(注意把表示对应顶点的字母写在对应的位置上).
?2.按边、角、边的顺序列出三个条件,用大括号合在一起.
?3.写出结论.每步要有推理的依据.
已知:如图,MA=NB,MC=ND,∠M=∠N.
求证:AB=CD.
课堂练习
F
A
B
D
C
E
点E、F在AC上,AD//BC,AD=CB,AE=CF
求证:△AFD≌△CEB
课堂练习
综合提高
已知:AB=AD,CB=CD.
求证:AC⊥BD.
如右图,
如图,在△ABC
和△ABD
中,
AB
=AB,AC
=
AD,∠B
=∠B,
但△ABC
和△ABD
不全等.
探索“SSA”能否识别两三角形全等
问题3
两边一角分别相等包括“两边夹角”和
“两边及其中一边的对角”分别相等两种情况,前面已
探索出“SAS”判定三角形全等的方法,那么由“SSA”
的条件能判定两个三角形全等吗?
A
B
C
D
三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。
A
B
C
D
E
F
在△ABC和△
DEF中
∴
△ABC
≌△
DEF(SSS)
AB=DE
BC=EF
CA=FD
用符号语言表达为:
三角形全等判定方法1
知识梳理:
三角形全等判定方法2
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS)
两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)
知识梳理:
F
E
D
C
B
A
AC=DF
∠C=∠F
BC=EF
知识梳理:
A
B
D
A
B
C
SSA不能判定全等
课堂练习
1、已知:如图,AB=AD,AC=AE,∠1=∠2.
求证:△ABC≌△ADE.
1
2
2、已知:如图,点A、B、C、D在同一条直线上,AC=DB,AE=DF,EA⊥AD,FD⊥AD,垂足分别是A,D。
求证:△EAB≌△FDC
A
E
B
C
D
F
3、已知:如图,AB=AC,AD=AE,∠1=∠2,
求证:△ABD≌△ACE
A
C
B
E
D
