沪科版九年级数学下册课件:24.1 第2课时 中心对称(共16张ppt)
文档属性
| 名称 | 沪科版九年级数学下册课件:24.1 第2课时 中心对称(共16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 218.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览



文档简介
第24章 圆
24.1 第2课时 中心对称
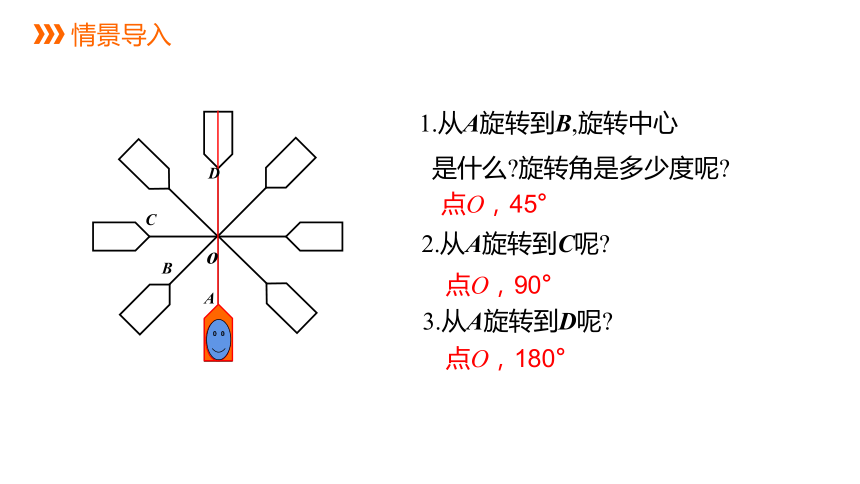
情景导入
1.从A旋转到B,旋转中心
是什么?旋转角是多少度呢?
2.从A旋转到C呢?
3.从A旋转到D呢?
点O,45°
点O,90°
点O,180°
o
A
B
C
D
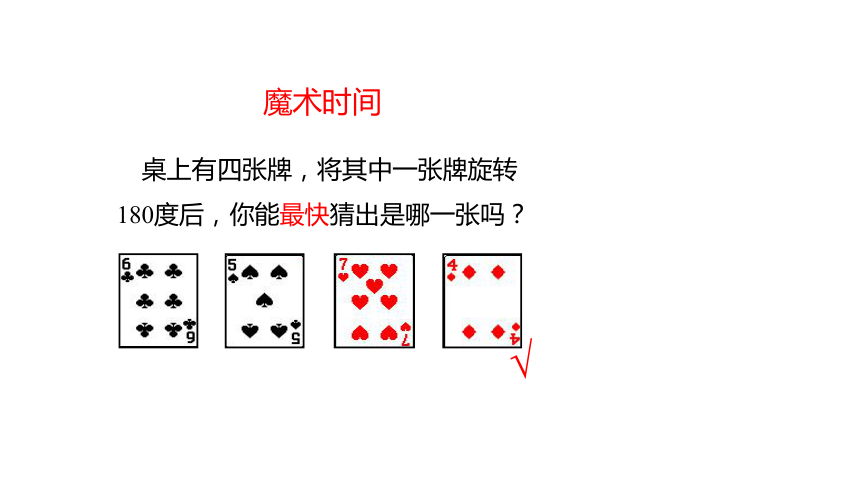
魔术时间
√
桌上有四张牌,将其中一张牌旋转180度后,你能最快猜出是哪一张吗?
获取新知
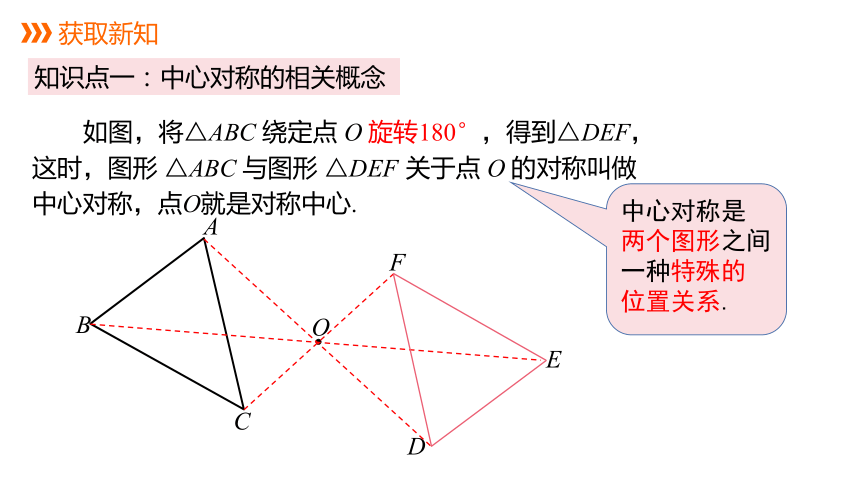
如图,将△ABC 绕定点 O 旋转180°,得到△DEF,这时,图形 △ABC 与图形 △DEF 关于点 O 的对称叫做中心对称,点O就是对称中心.
A
B
C
D
E
F
O
知识点一:中心对称的相关概念
中心对称是
两个图形之间
一种特殊的
位置关系.
成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心所平分.(即每组对应点与对称中心三点共线)
中心对称的性质:
由旋转角和旋转的性质很容易得到,你明白了吗?
例题讲解
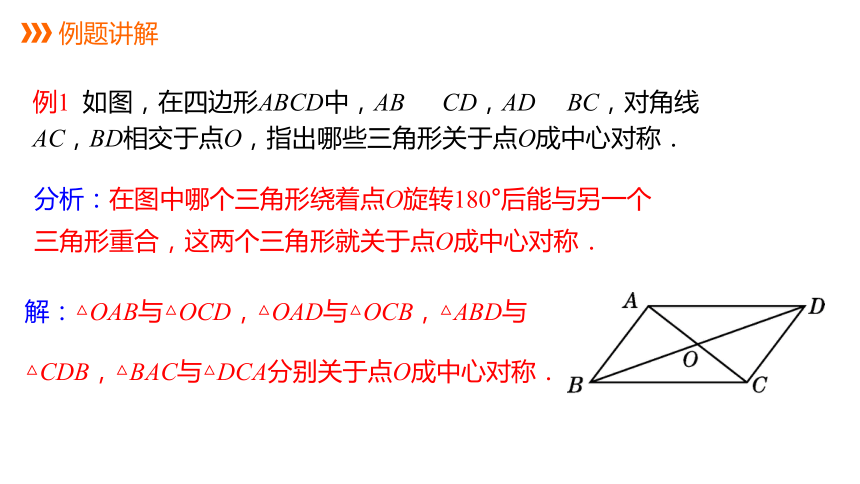
例1 如图,在四边形ABCD中,AB CD,AD BC,对角线AC,BD相交于点O,指出哪些三角形关于点O成中心对称.
解:△OAB与△OCD,△OAD与△OCB,△ABD与△CDB,△BAC与△DCA分别关于点O成中心对称.
分析:在图中哪个三角形绕着点O旋转180°后能与另一个
三角形重合,这两个三角形就关于点O成中心对称.
例2 如图,已知四边形 ABCD 和点O,试画出四边形ABCD 关于点 O 成中心对称的图形 A'B'C'D'.
分析:要画出四边形ABCD关于点O成中心对称的图形,只要画出A,B,C,D四点关于点O的对应点,再顺次连接各对应点即可.
A
B
C
D
O
作法:
1. 连接AO并延长到A',使OA'=OA,得到点A的对应点A';
2. 同理,可作出点B,C,D的对应点B',C',D';
3. 顺次连接A',B',C',D'.
则四边形A'B'C'D'即为所作.
A
B
C
D
O
A'
B'
C'
D'
知识点二:中心对称作图
获取新知
步骤:(1)确定对称中心和图形上的关键点.
(2)作各关键点的对应点:连接图形上每个关键点与对
称中心,并在延长线上截取对应连线的一倍即得到
关键点的对应点.
(3)按照原图顺序,顺次连接各对应点,即得到图形关
于对称中心的对称图形.
随堂演练
1.下列说法正确的是( )
A.全等的两个图形成中心对称
B.能够完全重合的两个图形成中心对称
C.绕某点旋转后能重合的两个图形成中心对称
D.绕某点旋转180°后能够重合的两个图形成中心对称
D
2.下列4组图形中,右边的图形与左边的图形成中心
对称的是( )
A
3.如图,△ABC与△A1B1C1关于点O成中心对称,下列说法:
①∠BAC=∠B1A1C1; ②AC=A1C1; ③OA=OA1;
④△ABC与△A1B1C1的面积相等,
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
D
4.如图, 在平面直角坐标系中, 若△ABC与△A1B1C1关于E点成中心对称, 则对称中心E点的坐标是________.
(3,-1)
5. 如图,已知点M是△ABC的边BC的中点,点O是 △ABC外一点.
(1) 画△A′B′C′,使△A′B′C′与△ABC关于点M成中心对称;
(2) 画△A″B″C″,使△A″B″C″与△ABC关于点O成中心对称.
解:(1)①连接AM并延长至A′,使A′M=AM;
②点B关于点M的对称点B′即为点C,点C关
于点M的对称点C′即为点B;
③连接A′B′,A′C′,△A′B′C′即为所求.
(2)①连接AO,BO,CO,并分别延长至A″,B″,
C″,使A″O=AO,B″O=BO,C″O=CO;
②连接A″B″,A″C″,B″C″,则△A″B″C″即为所求.
课堂小结
旋转
定义
三要素:旋转中心,旋转方向和旋转角度
性质
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
24.1 第2课时 中心对称
情景导入
1.从A旋转到B,旋转中心
是什么?旋转角是多少度呢?
2.从A旋转到C呢?
3.从A旋转到D呢?
点O,45°
点O,90°
点O,180°
o
A
B
C
D
魔术时间
√
桌上有四张牌,将其中一张牌旋转180度后,你能最快猜出是哪一张吗?
获取新知
如图,将△ABC 绕定点 O 旋转180°,得到△DEF,这时,图形 △ABC 与图形 △DEF 关于点 O 的对称叫做中心对称,点O就是对称中心.
A
B
C
D
E
F
O
知识点一:中心对称的相关概念
中心对称是
两个图形之间
一种特殊的
位置关系.
成中心对称的两个图形中,对应点的连线经过对称中心,且被对称中心所平分.(即每组对应点与对称中心三点共线)
中心对称的性质:
由旋转角和旋转的性质很容易得到,你明白了吗?
例题讲解
例1 如图,在四边形ABCD中,AB CD,AD BC,对角线AC,BD相交于点O,指出哪些三角形关于点O成中心对称.
解:△OAB与△OCD,△OAD与△OCB,△ABD与△CDB,△BAC与△DCA分别关于点O成中心对称.
分析:在图中哪个三角形绕着点O旋转180°后能与另一个
三角形重合,这两个三角形就关于点O成中心对称.
例2 如图,已知四边形 ABCD 和点O,试画出四边形ABCD 关于点 O 成中心对称的图形 A'B'C'D'.
分析:要画出四边形ABCD关于点O成中心对称的图形,只要画出A,B,C,D四点关于点O的对应点,再顺次连接各对应点即可.
A
B
C
D
O
作法:
1. 连接AO并延长到A',使OA'=OA,得到点A的对应点A';
2. 同理,可作出点B,C,D的对应点B',C',D';
3. 顺次连接A',B',C',D'.
则四边形A'B'C'D'即为所作.
A
B
C
D
O
A'
B'
C'
D'
知识点二:中心对称作图
获取新知
步骤:(1)确定对称中心和图形上的关键点.
(2)作各关键点的对应点:连接图形上每个关键点与对
称中心,并在延长线上截取对应连线的一倍即得到
关键点的对应点.
(3)按照原图顺序,顺次连接各对应点,即得到图形关
于对称中心的对称图形.
随堂演练
1.下列说法正确的是( )
A.全等的两个图形成中心对称
B.能够完全重合的两个图形成中心对称
C.绕某点旋转后能重合的两个图形成中心对称
D.绕某点旋转180°后能够重合的两个图形成中心对称
D
2.下列4组图形中,右边的图形与左边的图形成中心
对称的是( )
A
3.如图,△ABC与△A1B1C1关于点O成中心对称,下列说法:
①∠BAC=∠B1A1C1; ②AC=A1C1; ③OA=OA1;
④△ABC与△A1B1C1的面积相等,
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
D
4.如图, 在平面直角坐标系中, 若△ABC与△A1B1C1关于E点成中心对称, 则对称中心E点的坐标是________.
(3,-1)
5. 如图,已知点M是△ABC的边BC的中点,点O是 △ABC外一点.
(1) 画△A′B′C′,使△A′B′C′与△ABC关于点M成中心对称;
(2) 画△A″B″C″,使△A″B″C″与△ABC关于点O成中心对称.
解:(1)①连接AM并延长至A′,使A′M=AM;
②点B关于点M的对称点B′即为点C,点C关
于点M的对称点C′即为点B;
③连接A′B′,A′C′,△A′B′C′即为所求.
(2)①连接AO,BO,CO,并分别延长至A″,B″,
C″,使A″O=AO,B″O=BO,C″O=CO;
②连接A″B″,A″C″,B″C″,则△A″B″C″即为所求.
课堂小结
旋转
定义
三要素:旋转中心,旋转方向和旋转角度
性质
旋转前后的图形全等;
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
