沪科版九年级数学下册课件:24.3 第1课时 圆周角定理及其推论(共24张ppt)
文档属性
| 名称 | 沪科版九年级数学下册课件:24.3 第1课时 圆周角定理及其推论(共24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 385.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 09:14:36 | ||
图片预览


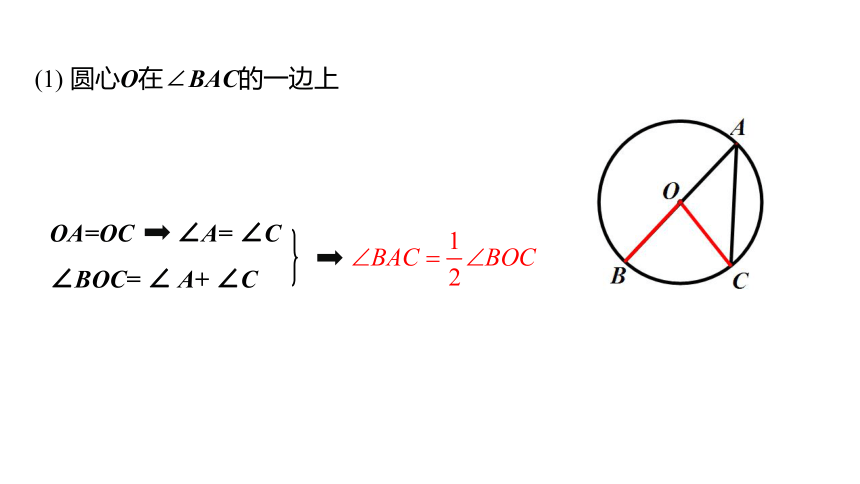
文档简介
第24章 圆
24.3 第1课时 圆周角定理及其推论
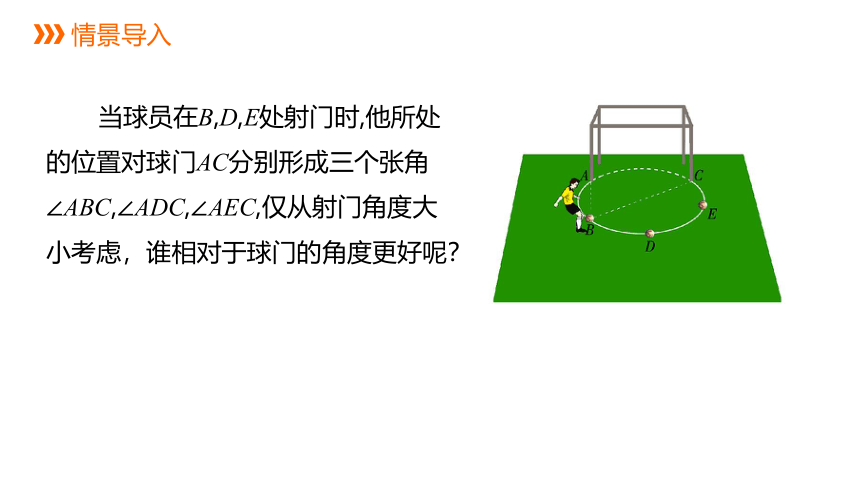
情景导入
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC,仅从射门角度大小考虑,谁相对于球门的角度更好呢?
知识回顾
问题1 什么是圆心角?
顶点在圆心的角叫圆心角,如∠BOC.
问题2 圆心角的度数与它所对弧的度数是什么关系?
圆心角的度数和它所对的弧的度数相等.
.
O
B
C
获取新知
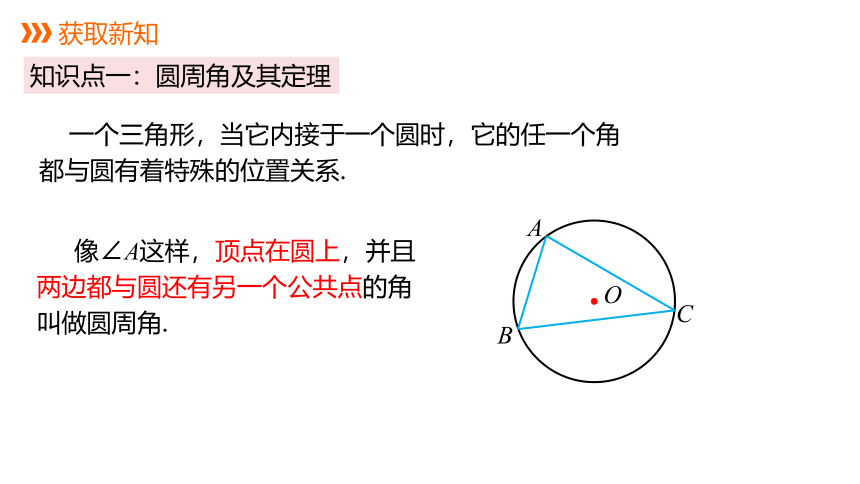
知识点一:圆周角及其定理
像∠A这样,顶点在圆上,并且两边都与圆还有另一个公共点的角叫做圆周角.
一个三角形,当它内接于一个圆时,它的任一个角都与圆有着特殊的位置关系.
O
A
B
C
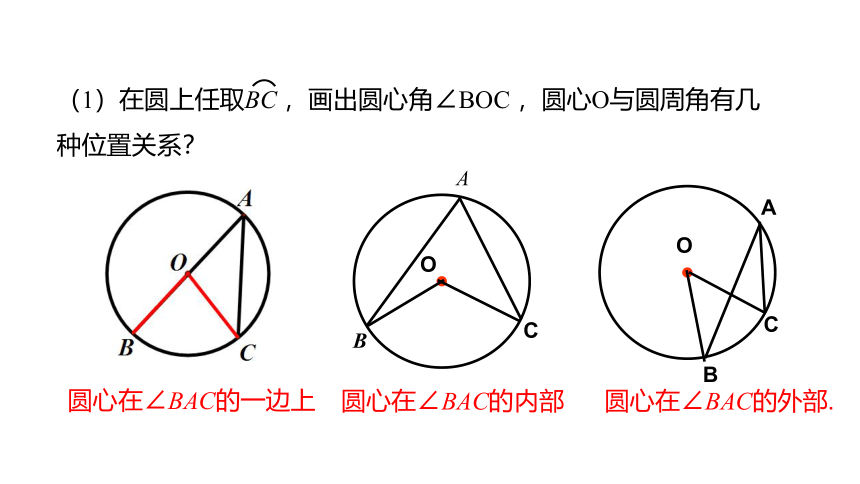
(1)在圆上任取BC ,画出圆心角∠BOC ,圆心O与圆周角有几种位置关系?
︵
圆心在∠BAC的一边上
圆心在∠BAC的内部
O
A
B
C
圆心在∠BAC的外部.
C
O
A
B
(1) 圆心O在∠BAC的一边上
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
O
A
B
D
O
A
C
D
O
A
B
C
D
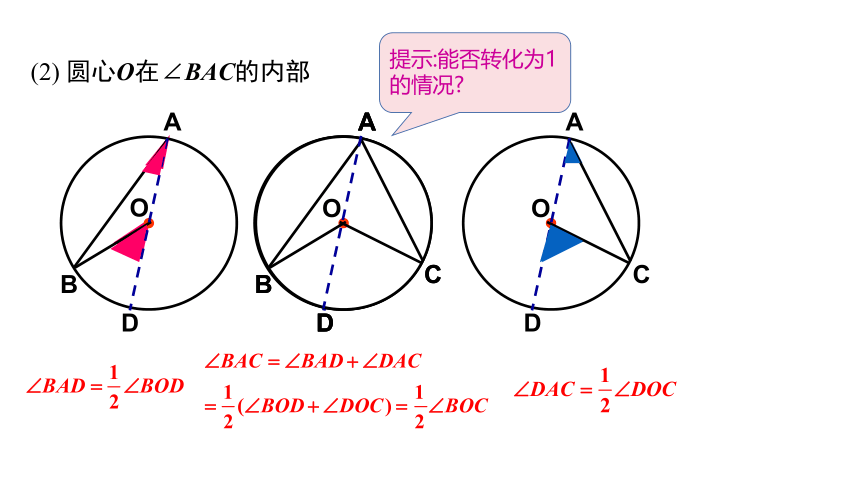
(2) 圆心O在∠BAC的内部
O
A
C
D
O
A
B
D
提示:能否转化为1的情况?
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
C
O
A
D
O
A
B
D
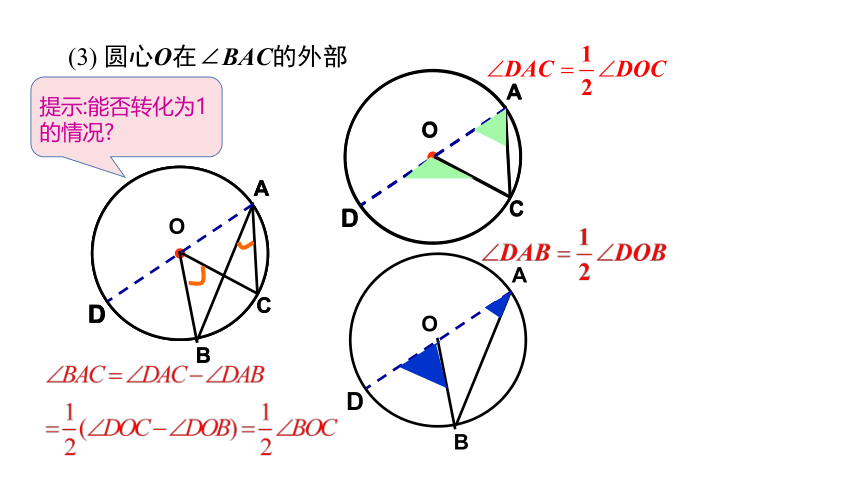
(3) 圆心O在∠BAC的外部
提示:能否转化为1的情况?
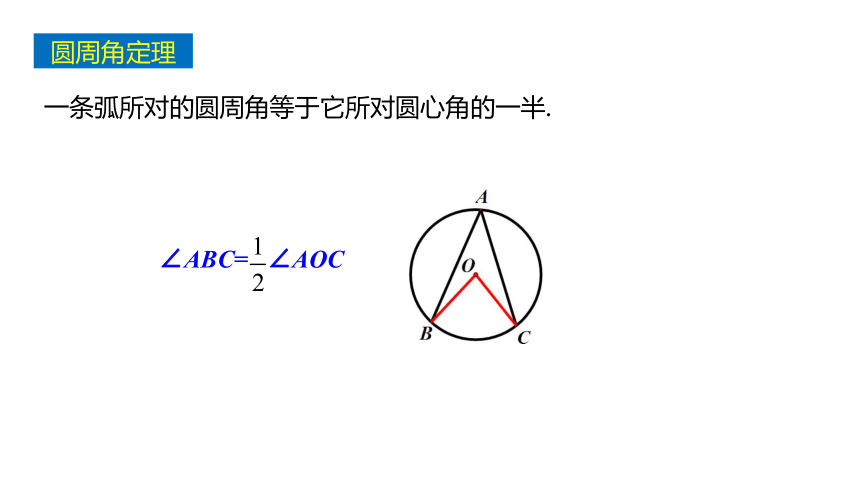
一条弧所对的圆周角等于它所对圆心角的一半.
圆周角定理
∠ABC= ∠AOC
例题讲解
例1 如图,在⊙O中,∠AOC=150°,求∠ABC,∠ADC的度数,并判断∠ABC和∠ADC,∠EBC和∠ADC之间的度数关系.
解:∵∠AOC=150°,∴∠ABC= ∠AOC=75°.
∵∠α=360°-∠AOC=360°-150°=210°,
∴∠ADC= ∠α=105°.
∵∠EBC=180°-∠ABC=180°-75°=105°,
∴∠EBC=∠ADC,即∠EBC与∠ADC相等.
又∵∠ABC+∠ADC=75°+105°=180°,
∴∠ABC和∠ADC互补.
获取新知
知识点二:圆周角定理的推论
圆周角定理推论1
在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等.
O
A1
A2
A3
A
C
B
D
A
B
O
C
E
F
圆心角相等
弧
相等
弦
相等
弦心距相等
圆周角相等
半圆或直径所对的圆周角是直角; 90°的圆周角所对的弦是直径.
圆周角定理推论2
理由:
1.直径所对的半圆所对的圆心角是180°;
2.圆心角是180°所对应的弦是直径;
3.圆周角等于所对弧上的圆心角的一半
例题讲解
例2 如图,AB为⊙O的直径,弦CD交AB于点P,
∠ACD = 60°,∠ADC =70°,求∠APC的度数.
分析:∠APC等于圆周角∠BAD与∠ADC之和.
解:连接BC,如图,则∠ACB=90°,
∠DCB =∠ACB-∠ACD
=90°-60°=30°.
又∵∠BAD=∠DCB=30°,
∴∠APC =∠BAD +∠ADC
=30°+70°=100°.
. O
A
D
C
P
B
由直径联想到直角时常见思路
例3 小明想用直角尺检査某些工件是否恰好为半圆形.
下面所示的四种圆弧形,你能判断哪个是半圆形?为什么?
解:题图(2)是半圆形.
∵90°的圆周角所对的弦是直径.
随堂演练
1.如图,△ABC是⊙O的内接三角形,若∠ABC =70°,则∠AOC的度数等于( )
A.140° B.130°
C.120° D.110°
A
O
C
B
A
2.如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )
A.30° B.40° C.50° D.60°
A
3. 如图,AB是⊙O的直径,BC是⊙O的弦,若∠OBC=60°,则∠BAC的度数是( )
A.75°
B.60°
C. 45°
D.30°
D
4. 如图,半径为5的⊙A经过点C和点O,点B是y轴右侧⊙A的优弧上一点,∠OBC=30°,则点C的坐标为( )
A
5.如图,点A、B、C、D在☉O上,点A与点D在点B、C所在直线的同侧,∠BAC=35?.
(1)∠BOC= ?,理由
是 ;
(2)∠BDC= ?,理由是 .
70
35
同弧所对的圆周角相等
一条弧所对的圆周角等于该弧所对的圆心角的一半
6. 如图,边长为 1 的小正方形构成的网格中,半径为1 的 ⊙O 的圆心 O 在格点上,则 ∠AED 的正切值等于 .
7.如图所示,已知四边形ABCD的四个顶点均在☉O上,AB=BC,BD交AC于点E.求证:DB平分∠ADC.
证明:∵AB=BC,
∴AB=BC,
∴∠ADB=∠BDC,
即DB平分∠ADC.
︵
︵
8.如图,点A,B,D,E在⊙O上,弦AE,BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点.试判断AB,AC之间的大小关系,并给出证明.
解:(1)AB=AC.
证明如下:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°, 即AD⊥BC.
∵BD=DC,
∴AD垂直平分BC,
∴AB=AC.
课堂小结
圆
周
角
定义
定理
推论
1.顶点在圆上;
2.两边都与圆相交的角
二者必须同时具备
一条弧所对的圆周角等于它所对的圆心角的一半.
半圆或直径所对的圆周角是直角;
90°的圆周角所对的弦是直径.
在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等.
圆心角
相等
弦
相等
弧
相等
弦心距
相等
圆心角
相等
24.3 第1课时 圆周角定理及其推论
情景导入
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC,∠ADC,∠AEC,仅从射门角度大小考虑,谁相对于球门的角度更好呢?
知识回顾
问题1 什么是圆心角?
顶点在圆心的角叫圆心角,如∠BOC.
问题2 圆心角的度数与它所对弧的度数是什么关系?
圆心角的度数和它所对的弧的度数相等.
.
O
B
C
获取新知
知识点一:圆周角及其定理
像∠A这样,顶点在圆上,并且两边都与圆还有另一个公共点的角叫做圆周角.
一个三角形,当它内接于一个圆时,它的任一个角都与圆有着特殊的位置关系.
O
A
B
C
(1)在圆上任取BC ,画出圆心角∠BOC ,圆心O与圆周角有几种位置关系?
︵
圆心在∠BAC的一边上
圆心在∠BAC的内部
O
A
B
C
圆心在∠BAC的外部.
C
O
A
B
(1) 圆心O在∠BAC的一边上
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
O
A
B
D
O
A
C
D
O
A
B
C
D
(2) 圆心O在∠BAC的内部
O
A
C
D
O
A
B
D
提示:能否转化为1的情况?
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
C
O
A
D
O
A
B
D
(3) 圆心O在∠BAC的外部
提示:能否转化为1的情况?
一条弧所对的圆周角等于它所对圆心角的一半.
圆周角定理
∠ABC= ∠AOC
例题讲解
例1 如图,在⊙O中,∠AOC=150°,求∠ABC,∠ADC的度数,并判断∠ABC和∠ADC,∠EBC和∠ADC之间的度数关系.
解:∵∠AOC=150°,∴∠ABC= ∠AOC=75°.
∵∠α=360°-∠AOC=360°-150°=210°,
∴∠ADC= ∠α=105°.
∵∠EBC=180°-∠ABC=180°-75°=105°,
∴∠EBC=∠ADC,即∠EBC与∠ADC相等.
又∵∠ABC+∠ADC=75°+105°=180°,
∴∠ABC和∠ADC互补.
获取新知
知识点二:圆周角定理的推论
圆周角定理推论1
在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等.
O
A1
A2
A3
A
C
B
D
A
B
O
C
E
F
圆心角相等
弧
相等
弦
相等
弦心距相等
圆周角相等
半圆或直径所对的圆周角是直角; 90°的圆周角所对的弦是直径.
圆周角定理推论2
理由:
1.直径所对的半圆所对的圆心角是180°;
2.圆心角是180°所对应的弦是直径;
3.圆周角等于所对弧上的圆心角的一半
例题讲解
例2 如图,AB为⊙O的直径,弦CD交AB于点P,
∠ACD = 60°,∠ADC =70°,求∠APC的度数.
分析:∠APC等于圆周角∠BAD与∠ADC之和.
解:连接BC,如图,则∠ACB=90°,
∠DCB =∠ACB-∠ACD
=90°-60°=30°.
又∵∠BAD=∠DCB=30°,
∴∠APC =∠BAD +∠ADC
=30°+70°=100°.
. O
A
D
C
P
B
由直径联想到直角时常见思路
例3 小明想用直角尺检査某些工件是否恰好为半圆形.
下面所示的四种圆弧形,你能判断哪个是半圆形?为什么?
解:题图(2)是半圆形.
∵90°的圆周角所对的弦是直径.
随堂演练
1.如图,△ABC是⊙O的内接三角形,若∠ABC =70°,则∠AOC的度数等于( )
A.140° B.130°
C.120° D.110°
A
O
C
B
A
2.如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )
A.30° B.40° C.50° D.60°
A
3. 如图,AB是⊙O的直径,BC是⊙O的弦,若∠OBC=60°,则∠BAC的度数是( )
A.75°
B.60°
C. 45°
D.30°
D
4. 如图,半径为5的⊙A经过点C和点O,点B是y轴右侧⊙A的优弧上一点,∠OBC=30°,则点C的坐标为( )
A
5.如图,点A、B、C、D在☉O上,点A与点D在点B、C所在直线的同侧,∠BAC=35?.
(1)∠BOC= ?,理由
是 ;
(2)∠BDC= ?,理由是 .
70
35
同弧所对的圆周角相等
一条弧所对的圆周角等于该弧所对的圆心角的一半
6. 如图,边长为 1 的小正方形构成的网格中,半径为1 的 ⊙O 的圆心 O 在格点上,则 ∠AED 的正切值等于 .
7.如图所示,已知四边形ABCD的四个顶点均在☉O上,AB=BC,BD交AC于点E.求证:DB平分∠ADC.
证明:∵AB=BC,
∴AB=BC,
∴∠ADB=∠BDC,
即DB平分∠ADC.
︵
︵
8.如图,点A,B,D,E在⊙O上,弦AE,BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点.试判断AB,AC之间的大小关系,并给出证明.
解:(1)AB=AC.
证明如下:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°, 即AD⊥BC.
∵BD=DC,
∴AD垂直平分BC,
∴AB=AC.
课堂小结
圆
周
角
定义
定理
推论
1.顶点在圆上;
2.两边都与圆相交的角
二者必须同时具备
一条弧所对的圆周角等于它所对的圆心角的一半.
半圆或直径所对的圆周角是直角;
90°的圆周角所对的弦是直径.
在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等.
圆心角
相等
弦
相等
弧
相等
弦心距
相等
圆心角
相等
