冀教版初中数学八年级上册 17.1 等腰三角形 课件(共29张ppt)
文档属性
| 名称 | 冀教版初中数学八年级上册 17.1 等腰三角形 课件(共29张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 608.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览






文档简介
等腰三角形性质定理
1. 等腰三角形的两个底角相等。(简称“等边对等角”)
2. 等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合。(简称“三线合一”)
等腰三角形
有两边相等的三角形叫等腰三角形。
边的问题,只能由边来
解决吗?
-----等腰三角形的判定
我们一起来探索:
判定等腰三角形,一定要测量边有多长吗?
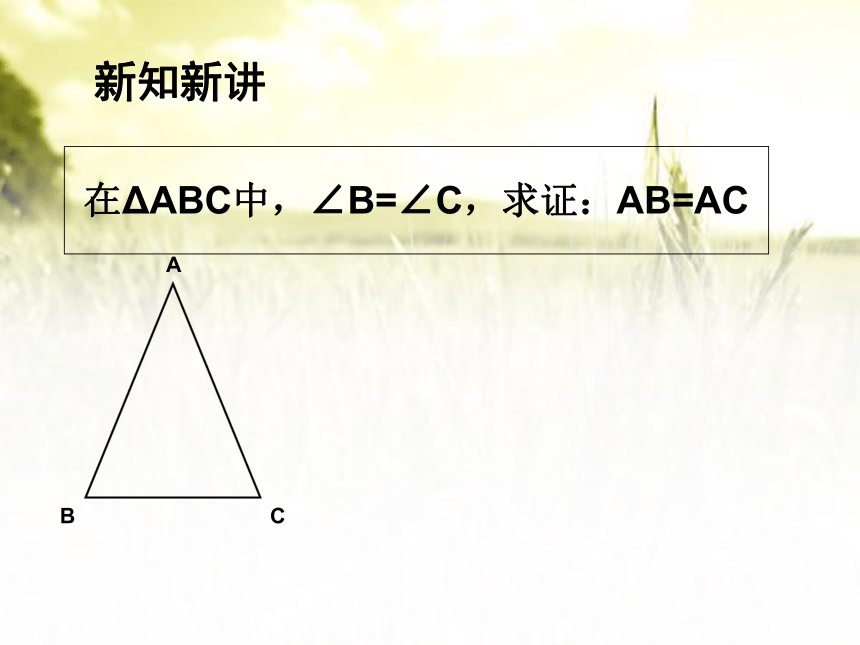
新知新讲
等角对等边
有等边对等角,
那是否有等角对等边呢?
在ΔABC中,∠B=∠C,求证:AB=AC
A
B
C
新知新讲
要点小测
已知一个三角形的两个角相等,要证明等角对等边,做辅助线时除了可以作两角公共边上的高线,还可以作( )
A 两角公共边上的中线
B 任意一角的角平分线
C 第三个角的角平分线
D 任意一边上的中线
C
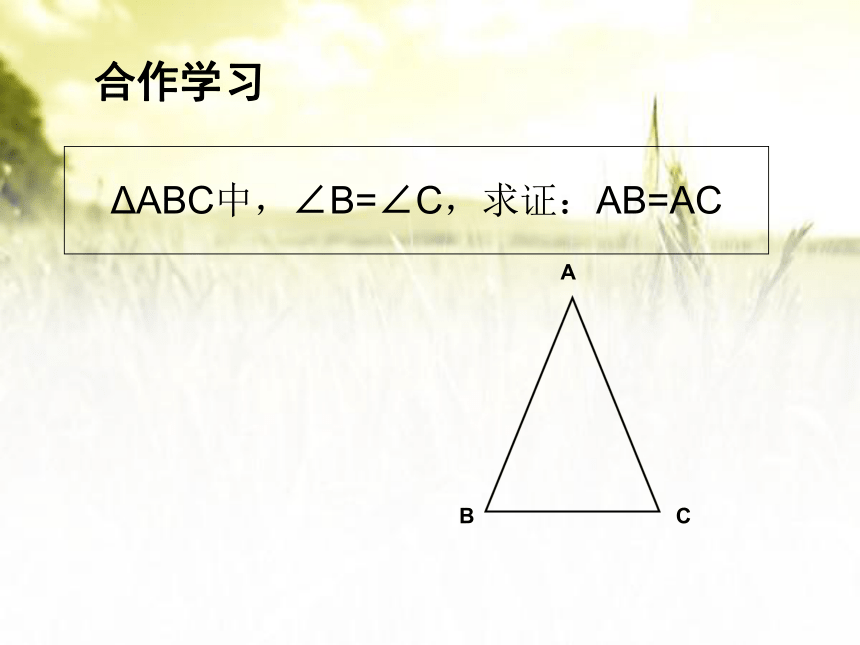
ΔABC中,∠B=∠C,求证:AB=AC
A
B
C
合作学习
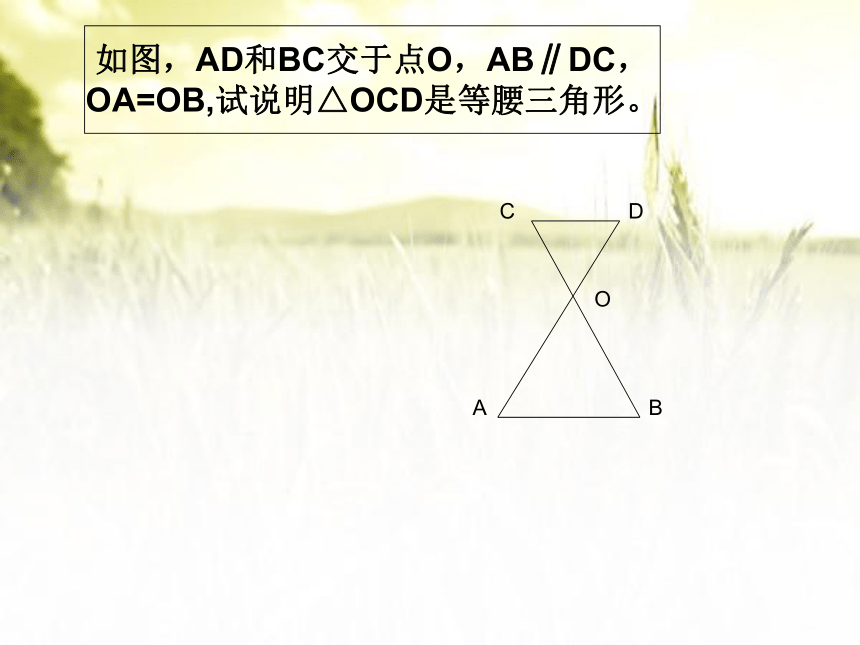
如图,AD和BC交于点O,AB∥DC,OA=OB,试说明△OCD是等腰三角形。
C
D
O
B
A
如果知道一个三角形是等腰三角形,会得到什么?
A 三角形全等
B 底角为60°
C 等边对等角
D 两底角不等
如图,AD和BC交于点O,AB∥DC,OA=OB,试说明△OCD是等腰三角形。
C
D
O
B
A
有方法更简单!
要证明一个三角形是等腰三角形,可考虑证明三角形中有两个内角相等,由等角对等边得到三角形两边相等,即此三角形是等腰三角形。
如图,已知BD平分∠ABC, ED∥BC,若BE=3,则ED=( )
A 3 B 4 C 1.5 D 2
温馨提示:
解决几何问题,边读题边在图上标注,
便于解题。
有方法更简单!
如图所示,
1.BD平分∠ABC;
2. ED∥BC;
3. △BED是等腰三角形。
以上三个条件,已知其中两个,可以推导出另外一个。
36
°
E
在△ABC中,已知 AB =AC , ∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论错误的是( )
A、 BD平分∠ABC
B、 △BCD的周长等于AB+BC
C、 AD=BD=BC
D、 点D是线段AC的中点
为什么说AD=BD?
A 由三角形全等而得
B 等角对等边
C 线段垂直平分线上一点
到线段两端的距离相等。
D 线段垂直平分线上一点
到线段任意两点的距离相等。
有方法更简单!
要证明三角形两边相等,可考虑下面两种方法:
1.利用等角对等边证明;
2.证明这两边的交点在第三边的垂直平分线上。
学习提醒
等腰三角形判定定理
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形,
两个相等的角所对的边相等。
(简称:等角对等边)
探索发现
三条边都相等的三角形是等边三角形.
(1)一个三角形满足什么条件时,会成为等边三角形?
①三个角都相等的三角形是等边三角形.
②有一个角等于60°的等腰三角形是等边三角形.
教学例2
1、已知底边及底边上的高,用尺规作等腰三角形.已知线段a和h.
求作:等腰三角形ABC,使BC=a,高AD=h.
(分析:先作出线段BC=a,再作出BC的垂直平分线.在这条垂直平分线上截取点A,使点A到BC的距离=h,连接相关点即得.) h
a
作法:
(1)作线段BC=a.
(2)作BC的垂直平分线MD,垂足为D.
(3)在DM上截取DA=h.
(4)连接AB、AC.
(5)ΔABC即为所求.
已知:△ABC是等边三角形,DE∥BC,
分别交AB、AC于点D,E.
求证:△ADE是等边三角形.
B
C
A
D
E
证明∵△ABC是等边三角形,
∴ ∠A=∠B=∠C=60°,
∵ DE∥BC,
∴∠ADE=∠B=60°,
∠AED=∠C=60°,
∴∠A=∠ADE=∠AED,
∴△ABC是等边三角形.
B
C
A
D
B
C
A
D
反馈运用
如图,BD是∠ ABC的角平分线,DE∥BC,交AB于点E。判断△ BDE是不是等腰三角形,并说明理由。
一变:如图,BD是等腰三角形ABC的底角∠ ABC的角平分线,DE∥BC,交AB于点E。判断△ BDE是不是等腰三角形,并说明理由。
合作探究
二变:在△ABC中,已知 AB =AC ,BO平分∠ABC ,CO平分∠ACB
①则△ OBC是 三角形
②过点O作DE∥BC,则图中有 个等腰三角形。
③猜想线段DE和线段DB,EC之间的关系?并说明理由。
DE=DB+CE
也可得:DE=2DB=2CE
B
O
C
A
等腰
5
D
E
三变:如果△ ABC不是等腰三角形, ∠ABC和∠ACB的角平分线相交于点O, DE∥BC。
① 则图中等腰三角形共有 个。
② 在图中,可得线段关系是 ( )
A、 DO+EO=BD+EC
B、 DO+EO>BD+EC
C、 DO+EO<BD+EC
D、 无法确定
③ 若BC=3,作OF∥AB,OG∥AC,
则△ OFG的周长= 。
A
E
C
O
B
D
C
O
E
C
F
G
2
A
3
1.下列能断定△ABC为等腰三角形的是( )
A.∠A=30°,∠B=60°
B.∠A=50°,∠B=80°
C.AB=AC=2,BC=4
D.AB=3,BC=7,△ABC的周长为10
2.如图所示,∠A=36°,∠ADB=108°, 则图中共有等腰三角形( )
A.1个 B.2个 C.3个 D.4个
3.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于点M,交AC于点N,若BM+CN=9,则线段MN的长为( )
A.6 B.7 C.8 D.9
课堂小测
B
A
D
4.等腰三角形△ABC中,∠A的外角是
110°,则∠B=
5.如图,AB=AC,BD平分∠ABC,且 ∠C=2∠A, 则图中等腰三角形 共有 个。
6.AB=AC,BF 平分∠ABC交AC于F,CE平分∠ACB交AB于E,
BF和BE交于点D,且EF∥BC,则图中有 个等腰三角形。
A
B
C
D
70°或 55°
3
6
1.如图,GF⊥AF于F,且AB=BC=CD=DE=EF=FG,
求∠A的度数。
2.如图,AD平分△ABC的外角∠EAC,AD//BC,则△ ABC是等腰三角形吗?说明你的理由。
证明:∵AD∥BC,
∴∠1=∠B,
∠2=∠C,
∵ ∠1=∠2,
∴∠B=∠C,
∴AB=AC
本课小结:
通过本节课的学习,你有何收获?
1. 等腰三角形的两个底角相等。(简称“等边对等角”)
2. 等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合。(简称“三线合一”)
等腰三角形
有两边相等的三角形叫等腰三角形。
边的问题,只能由边来
解决吗?
-----等腰三角形的判定
我们一起来探索:
判定等腰三角形,一定要测量边有多长吗?
新知新讲
等角对等边
有等边对等角,
那是否有等角对等边呢?
在ΔABC中,∠B=∠C,求证:AB=AC
A
B
C
新知新讲
要点小测
已知一个三角形的两个角相等,要证明等角对等边,做辅助线时除了可以作两角公共边上的高线,还可以作( )
A 两角公共边上的中线
B 任意一角的角平分线
C 第三个角的角平分线
D 任意一边上的中线
C
ΔABC中,∠B=∠C,求证:AB=AC
A
B
C
合作学习
如图,AD和BC交于点O,AB∥DC,OA=OB,试说明△OCD是等腰三角形。
C
D
O
B
A
如果知道一个三角形是等腰三角形,会得到什么?
A 三角形全等
B 底角为60°
C 等边对等角
D 两底角不等
如图,AD和BC交于点O,AB∥DC,OA=OB,试说明△OCD是等腰三角形。
C
D
O
B
A
有方法更简单!
要证明一个三角形是等腰三角形,可考虑证明三角形中有两个内角相等,由等角对等边得到三角形两边相等,即此三角形是等腰三角形。
如图,已知BD平分∠ABC, ED∥BC,若BE=3,则ED=( )
A 3 B 4 C 1.5 D 2
温馨提示:
解决几何问题,边读题边在图上标注,
便于解题。
有方法更简单!
如图所示,
1.BD平分∠ABC;
2. ED∥BC;
3. △BED是等腰三角形。
以上三个条件,已知其中两个,可以推导出另外一个。
36
°
E
在△ABC中,已知 AB =AC , ∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,下述结论错误的是( )
A、 BD平分∠ABC
B、 △BCD的周长等于AB+BC
C、 AD=BD=BC
D、 点D是线段AC的中点
为什么说AD=BD?
A 由三角形全等而得
B 等角对等边
C 线段垂直平分线上一点
到线段两端的距离相等。
D 线段垂直平分线上一点
到线段任意两点的距离相等。
有方法更简单!
要证明三角形两边相等,可考虑下面两种方法:
1.利用等角对等边证明;
2.证明这两边的交点在第三边的垂直平分线上。
学习提醒
等腰三角形判定定理
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形,
两个相等的角所对的边相等。
(简称:等角对等边)
探索发现
三条边都相等的三角形是等边三角形.
(1)一个三角形满足什么条件时,会成为等边三角形?
①三个角都相等的三角形是等边三角形.
②有一个角等于60°的等腰三角形是等边三角形.
教学例2
1、已知底边及底边上的高,用尺规作等腰三角形.已知线段a和h.
求作:等腰三角形ABC,使BC=a,高AD=h.
(分析:先作出线段BC=a,再作出BC的垂直平分线.在这条垂直平分线上截取点A,使点A到BC的距离=h,连接相关点即得.) h
a
作法:
(1)作线段BC=a.
(2)作BC的垂直平分线MD,垂足为D.
(3)在DM上截取DA=h.
(4)连接AB、AC.
(5)ΔABC即为所求.
已知:△ABC是等边三角形,DE∥BC,
分别交AB、AC于点D,E.
求证:△ADE是等边三角形.
B
C
A
D
E
证明∵△ABC是等边三角形,
∴ ∠A=∠B=∠C=60°,
∵ DE∥BC,
∴∠ADE=∠B=60°,
∠AED=∠C=60°,
∴∠A=∠ADE=∠AED,
∴△ABC是等边三角形.
B
C
A
D
B
C
A
D
反馈运用
如图,BD是∠ ABC的角平分线,DE∥BC,交AB于点E。判断△ BDE是不是等腰三角形,并说明理由。
一变:如图,BD是等腰三角形ABC的底角∠ ABC的角平分线,DE∥BC,交AB于点E。判断△ BDE是不是等腰三角形,并说明理由。
合作探究
二变:在△ABC中,已知 AB =AC ,BO平分∠ABC ,CO平分∠ACB
①则△ OBC是 三角形
②过点O作DE∥BC,则图中有 个等腰三角形。
③猜想线段DE和线段DB,EC之间的关系?并说明理由。
DE=DB+CE
也可得:DE=2DB=2CE
B
O
C
A
等腰
5
D
E
三变:如果△ ABC不是等腰三角形, ∠ABC和∠ACB的角平分线相交于点O, DE∥BC。
① 则图中等腰三角形共有 个。
② 在图中,可得线段关系是 ( )
A、 DO+EO=BD+EC
B、 DO+EO>BD+EC
C、 DO+EO<BD+EC
D、 无法确定
③ 若BC=3,作OF∥AB,OG∥AC,
则△ OFG的周长= 。
A
E
C
O
B
D
C
O
E
C
F
G
2
A
3
1.下列能断定△ABC为等腰三角形的是( )
A.∠A=30°,∠B=60°
B.∠A=50°,∠B=80°
C.AB=AC=2,BC=4
D.AB=3,BC=7,△ABC的周长为10
2.如图所示,∠A=36°,∠ADB=108°, 则图中共有等腰三角形( )
A.1个 B.2个 C.3个 D.4个
3.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于点M,交AC于点N,若BM+CN=9,则线段MN的长为( )
A.6 B.7 C.8 D.9
课堂小测
B
A
D
4.等腰三角形△ABC中,∠A的外角是
110°,则∠B=
5.如图,AB=AC,BD平分∠ABC,且 ∠C=2∠A, 则图中等腰三角形 共有 个。
6.AB=AC,BF 平分∠ABC交AC于F,CE平分∠ACB交AB于E,
BF和BE交于点D,且EF∥BC,则图中有 个等腰三角形。
A
B
C
D
70°或 55°
3
6
1.如图,GF⊥AF于F,且AB=BC=CD=DE=EF=FG,
求∠A的度数。
2.如图,AD平分△ABC的外角∠EAC,AD//BC,则△ ABC是等腰三角形吗?说明你的理由。
证明:∵AD∥BC,
∴∠1=∠B,
∠2=∠C,
∵ ∠1=∠2,
∴∠B=∠C,
∴AB=AC
本课小结:
通过本节课的学习,你有何收获?
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
