冀教版初中数学八年级上册 第十七章 特殊三角形复习 课件(共16张ppt)
文档属性
| 名称 | 冀教版初中数学八年级上册 第十七章 特殊三角形复习 课件(共16张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 491.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 09:22:53 | ||
图片预览



文档简介
学习目标
1、知识与能力 能利用等腰三角形、等边三角形、直角三角形的性质定理和判定定理解决实际问题
2、过程与方法 通过对特殊三角形的学习,进一步认识各类三角形,培养学生观察、类比的思维能力,体会数学知识在解决实际问题中的作用
3、情感态度与价值观 在探索三角形性质的过程中,感受数学逻辑推理的重要性,体会数学在现实生活中的广阔应用,提高数学的学习兴趣
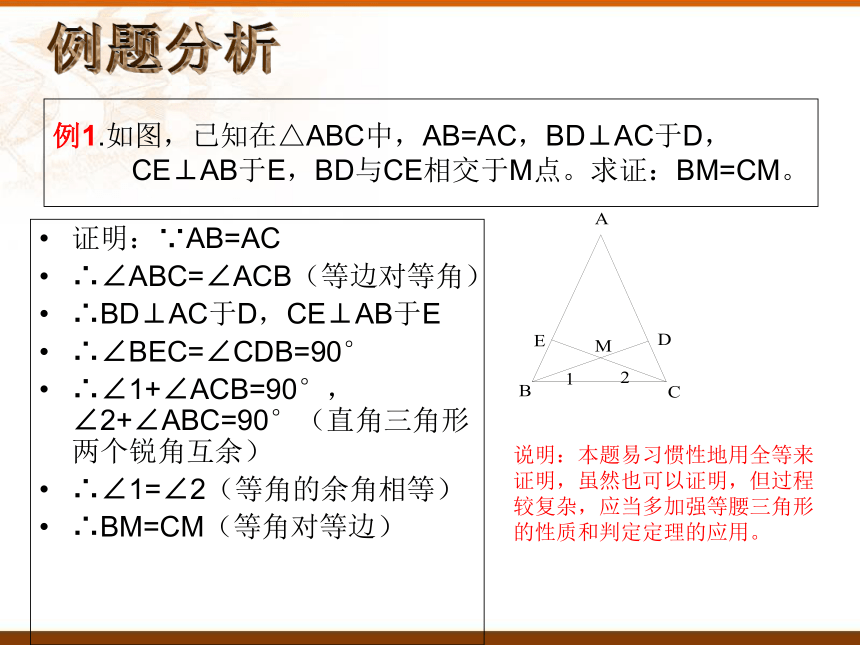
例1.如图,已知在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD与CE相交于M点。求证:BM=CM。
证明:∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∴BD⊥AC于D,CE⊥AB于E
∴∠BEC=∠CDB=90°
∴∠1+∠ACB=90°,∠2+∠ABC=90°(直角三角形两个锐角互余)
∴∠1=∠2(等角的余角相等)
∴BM=CM(等角对等边)
说明:本题易习惯性地用全等来证明,虽然也可以证明,但过程较复杂,应当多加强等腰三角形的性质和判定定理的应用。
例2.已知:如图,∠C=90°,BC=AC,D、E分别在BC和AC上,且BD=CE,M是AB的中点.
求证:△MDE是等腰三角形.
分析:要证△MDE是等腰三角形,只需证MD=ME。连结CM,可利用△BMD≌△CME得到结果。
证明:连结CM
∵∠C=90°,BC=AC
∴∠A=∠B=45°
∵M是AB的中点
∴CM平分∠BCA
(等腰三角形顶角的平分线和底边上的中线重合)
∴∠MCE=∠MCB=∠BCA=45°
∴∠B=∠MCE=∠MCB
∴CM=MB(等角对等边)
在△BDE和△CEM中
∴△BDM≌△CEM(SAS)
∴MD=ME
∴△MDE是等腰三角形
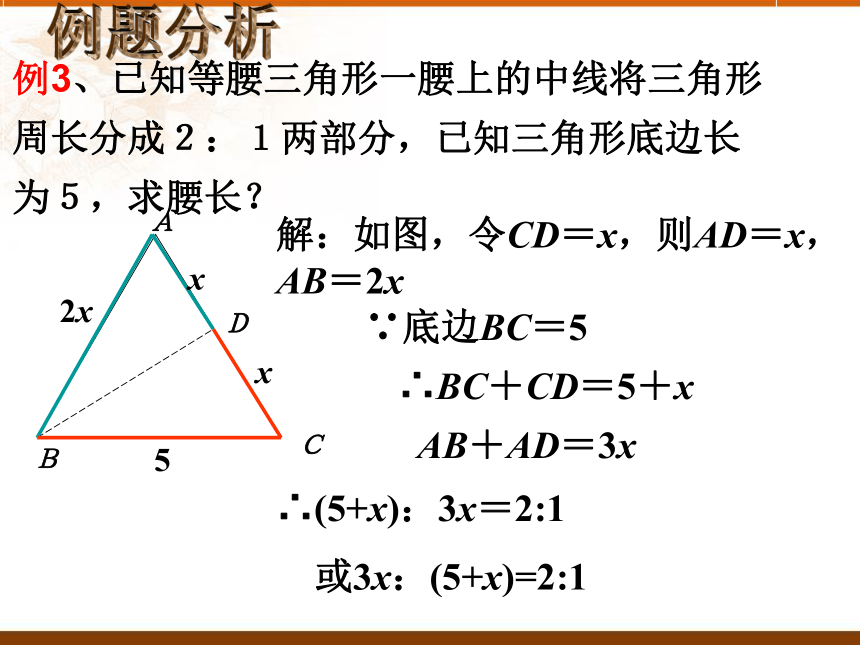
例3、已知等腰三角形一腰上的中线将三角形周长分成2:1两部分,已知三角形底边长为5,求腰长?
解:如图,令CD=x,则AD=x,AB=2x
∵底边BC=5
∴BC+CD=5+x
AB+AD=3x
∴(5+x):3x=2:1
或3x:(5+x)=2:1
A
B
C
D
x
x
2x
5
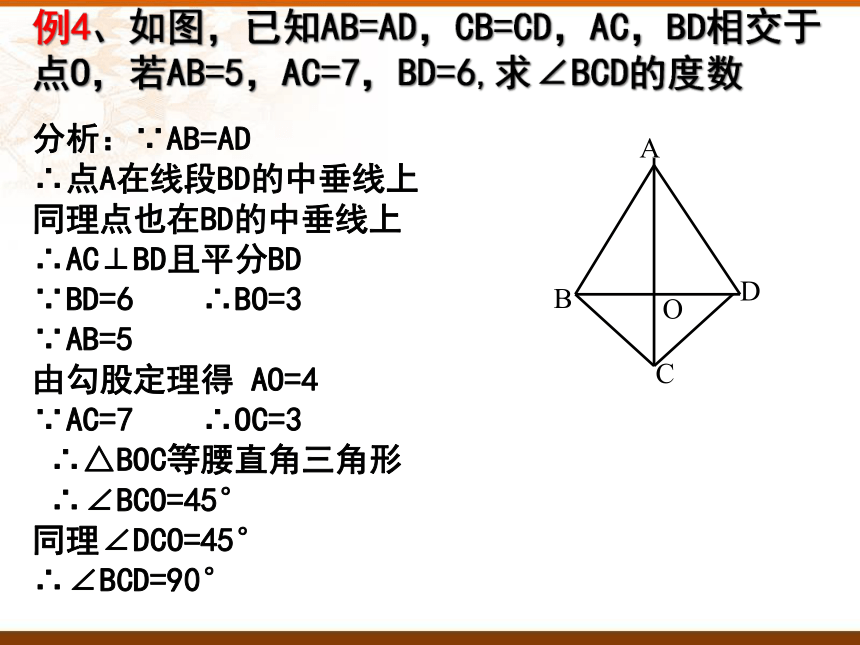
例4、如图,已知AB=AD,CB=CD,AC,BD相交于
点O,若AB=5,AC=7,BD=6,求∠BCD的度数
分析:∵AB=AD
∴点A在线段BD的中垂线上
同理点也在BD的中垂线上
∴AC⊥BD且平分BD
∵BD=6 ∴BO=3
∵AB=5
由勾股定理得 AO=4
∵AC=7 ∴OC=3
∴△BOC等腰直角三角形
∴∠BCO=45°
同理∠DCO=45°
∴∠BCD=90°
A
B
D
C
O
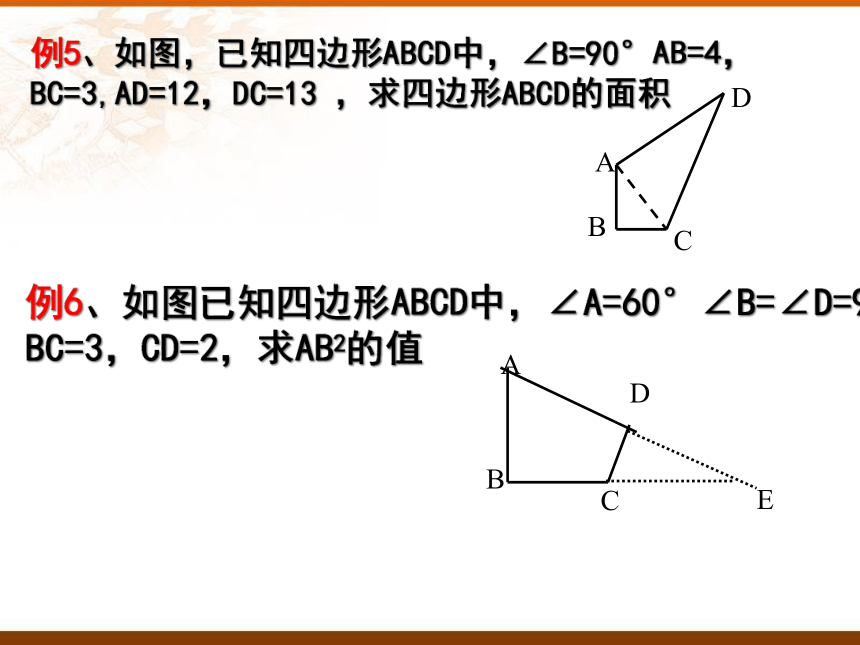
例5、如图,已知四边形ABCD中,∠B=90°AB=4,BC=3,AD=12,DC=13 ,求四边形ABCD的面积
A
B
C
D
A
B
C
D
E
例6、如图已知四边形ABCD中,∠A=60°∠B=∠D=90°,
BC=3,CD=2,求AB2的值
1. 下列结论叙述正确的个数为( )
( 1)等腰三角形高、中 线、角平分线重合;
( 2)等腰三角形两底角 的外角相等;?
( 3)等腰三角形有且只有一条对称轴;
( 4)有一个角等于60°的等腰三角形是等边三角形。
(A)0个 (B)1个 (C)2个 (D)3个
2、满足下列条件的ΔABC,不是直角三角形的是:( )
A、b2=a2-c2 B、 ∠C=∠A-∠B
C、∠A:∠B:∠C=3:4:5
D、a:b:c=12:13:15
3、下列条件中,不能判定两个直角三角形全等的是( )
A、一条直角边和一个锐角分别相等
B、两条直角边对应相等
C、斜边和一条直角边对应相等
D、两个锐角对应相等
?
5、如图,EA⊥AB,BC⊥AB,AB=AE=2BC,
D为AB的中点,有以下判断,(1)DE=AC (2)DE⊥AC,
(3) ∠CAB=30o (4) ∠EAF=∠ADE,期中正确
结论的个数是:( )
A、 一个 B、两个 C、三个 D、四个
6、如图,在ΔABC中,∠ACB=90o ,CD是高线,
E是AB上一点,且AE=AC,∠ACE:∠ACD=3:1,
则与∠DCE相等的角是( )
A 、∠A B、 ∠B C 、 ∠BCE D、以上都错
E
F
C
B
D
A
第三题
B
A
C
D
E
第四题
已知:如图,∠A=90°,∠B=15°,BD=DC.
请说明AC=BD的理由.
等腰三角形性质与判定的应用
(1)计算角的度数
利用等腰三角形的性质,结合三角形内角和定理及推论计算角的度数,是等腰三角形性质的重要应用。
①已知角的度数,求其它角的度数
②已知条件中有较多的等腰三角形(此时往往设法用未知数表示图中的角,从中得到含这些未知数的方程或方程组)
(2)证明线段或角相等
特殊三角形的性质与判定
1.性质
(1):等腰三角形的两个底角相等。
(2):等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。
2.判定
定义:有两边相等的三角形是等腰三角形。
判定定理:有两个角相等的三角形是等腰三角形。
等腰三角形:
1 , 三个角都相等的三角形是等边三角形。
2 , 有一个角等于60°的等腰三角形是等边三角形。
3 , 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半
第三步:由矛盾的结果,判定假设不成立,从而说明命题的结论是正确的.
用反证法证明一个命题是真命题的一般步骤.
第一步:假设命题的结论不成立.
第二步:从这个假设和其他已知条件出发,经过推理论证,得出与学过的概念、基本事实、已证明的定理、性质或题设条件相矛盾的结果.
直角三角形全等的判定方法:
A
B
C
A′
B′
C′
ASA, AAS
SAS
3) SSS
4) HL
1、知识与能力 能利用等腰三角形、等边三角形、直角三角形的性质定理和判定定理解决实际问题
2、过程与方法 通过对特殊三角形的学习,进一步认识各类三角形,培养学生观察、类比的思维能力,体会数学知识在解决实际问题中的作用
3、情感态度与价值观 在探索三角形性质的过程中,感受数学逻辑推理的重要性,体会数学在现实生活中的广阔应用,提高数学的学习兴趣
例1.如图,已知在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD与CE相交于M点。求证:BM=CM。
证明:∵AB=AC
∴∠ABC=∠ACB(等边对等角)
∴BD⊥AC于D,CE⊥AB于E
∴∠BEC=∠CDB=90°
∴∠1+∠ACB=90°,∠2+∠ABC=90°(直角三角形两个锐角互余)
∴∠1=∠2(等角的余角相等)
∴BM=CM(等角对等边)
说明:本题易习惯性地用全等来证明,虽然也可以证明,但过程较复杂,应当多加强等腰三角形的性质和判定定理的应用。
例2.已知:如图,∠C=90°,BC=AC,D、E分别在BC和AC上,且BD=CE,M是AB的中点.
求证:△MDE是等腰三角形.
分析:要证△MDE是等腰三角形,只需证MD=ME。连结CM,可利用△BMD≌△CME得到结果。
证明:连结CM
∵∠C=90°,BC=AC
∴∠A=∠B=45°
∵M是AB的中点
∴CM平分∠BCA
(等腰三角形顶角的平分线和底边上的中线重合)
∴∠MCE=∠MCB=∠BCA=45°
∴∠B=∠MCE=∠MCB
∴CM=MB(等角对等边)
在△BDE和△CEM中
∴△BDM≌△CEM(SAS)
∴MD=ME
∴△MDE是等腰三角形
例3、已知等腰三角形一腰上的中线将三角形周长分成2:1两部分,已知三角形底边长为5,求腰长?
解:如图,令CD=x,则AD=x,AB=2x
∵底边BC=5
∴BC+CD=5+x
AB+AD=3x
∴(5+x):3x=2:1
或3x:(5+x)=2:1
A
B
C
D
x
x
2x
5
例4、如图,已知AB=AD,CB=CD,AC,BD相交于
点O,若AB=5,AC=7,BD=6,求∠BCD的度数
分析:∵AB=AD
∴点A在线段BD的中垂线上
同理点也在BD的中垂线上
∴AC⊥BD且平分BD
∵BD=6 ∴BO=3
∵AB=5
由勾股定理得 AO=4
∵AC=7 ∴OC=3
∴△BOC等腰直角三角形
∴∠BCO=45°
同理∠DCO=45°
∴∠BCD=90°
A
B
D
C
O
例5、如图,已知四边形ABCD中,∠B=90°AB=4,BC=3,AD=12,DC=13 ,求四边形ABCD的面积
A
B
C
D
A
B
C
D
E
例6、如图已知四边形ABCD中,∠A=60°∠B=∠D=90°,
BC=3,CD=2,求AB2的值
1. 下列结论叙述正确的个数为( )
( 1)等腰三角形高、中 线、角平分线重合;
( 2)等腰三角形两底角 的外角相等;?
( 3)等腰三角形有且只有一条对称轴;
( 4)有一个角等于60°的等腰三角形是等边三角形。
(A)0个 (B)1个 (C)2个 (D)3个
2、满足下列条件的ΔABC,不是直角三角形的是:( )
A、b2=a2-c2 B、 ∠C=∠A-∠B
C、∠A:∠B:∠C=3:4:5
D、a:b:c=12:13:15
3、下列条件中,不能判定两个直角三角形全等的是( )
A、一条直角边和一个锐角分别相等
B、两条直角边对应相等
C、斜边和一条直角边对应相等
D、两个锐角对应相等
?
5、如图,EA⊥AB,BC⊥AB,AB=AE=2BC,
D为AB的中点,有以下判断,(1)DE=AC (2)DE⊥AC,
(3) ∠CAB=30o (4) ∠EAF=∠ADE,期中正确
结论的个数是:( )
A、 一个 B、两个 C、三个 D、四个
6、如图,在ΔABC中,∠ACB=90o ,CD是高线,
E是AB上一点,且AE=AC,∠ACE:∠ACD=3:1,
则与∠DCE相等的角是( )
A 、∠A B、 ∠B C 、 ∠BCE D、以上都错
E
F
C
B
D
A
第三题
B
A
C
D
E
第四题
已知:如图,∠A=90°,∠B=15°,BD=DC.
请说明AC=BD的理由.
等腰三角形性质与判定的应用
(1)计算角的度数
利用等腰三角形的性质,结合三角形内角和定理及推论计算角的度数,是等腰三角形性质的重要应用。
①已知角的度数,求其它角的度数
②已知条件中有较多的等腰三角形(此时往往设法用未知数表示图中的角,从中得到含这些未知数的方程或方程组)
(2)证明线段或角相等
特殊三角形的性质与判定
1.性质
(1):等腰三角形的两个底角相等。
(2):等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。
2.判定
定义:有两边相等的三角形是等腰三角形。
判定定理:有两个角相等的三角形是等腰三角形。
等腰三角形:
1 , 三个角都相等的三角形是等边三角形。
2 , 有一个角等于60°的等腰三角形是等边三角形。
3 , 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半
第三步:由矛盾的结果,判定假设不成立,从而说明命题的结论是正确的.
用反证法证明一个命题是真命题的一般步骤.
第一步:假设命题的结论不成立.
第二步:从这个假设和其他已知条件出发,经过推理论证,得出与学过的概念、基本事实、已证明的定理、性质或题设条件相矛盾的结果.
直角三角形全等的判定方法:
A
B
C
A′
B′
C′
ASA, AAS
SAS
3) SSS
4) HL
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
