人教版八年级上册数学课件:13.3.2等边三角形(共19张ppt)
文档属性
| 名称 | 人教版八年级上册数学课件:13.3.2等边三角形(共19张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 09:33:59 | ||
图片预览


文档简介
13.3.2 等边三角形
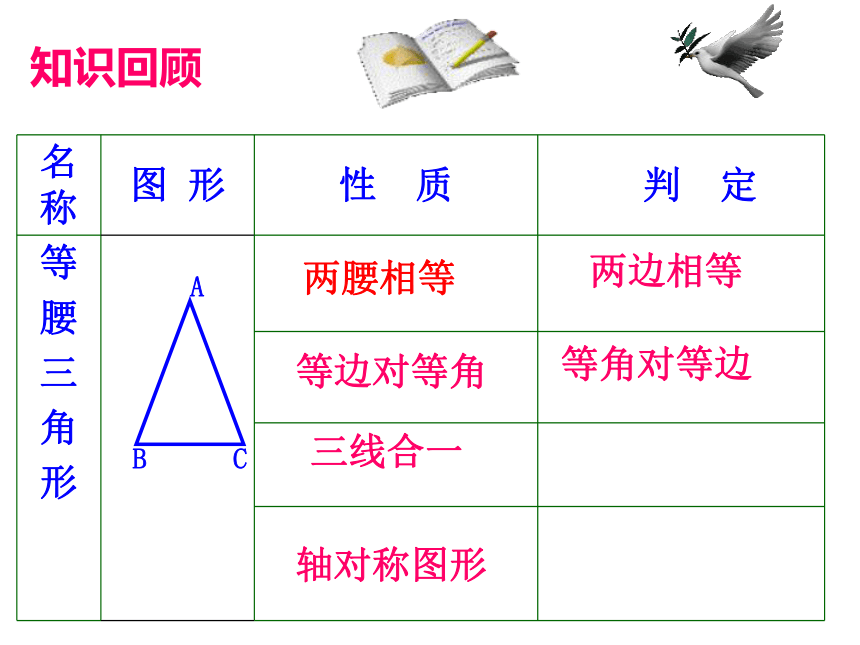
名称
图 形
性 质
判 定
等
腰
三
角
形
A
B
C
等边对等角
三线合一
等角对等边
两边相等
两腰相等
轴对称图形
知识回顾
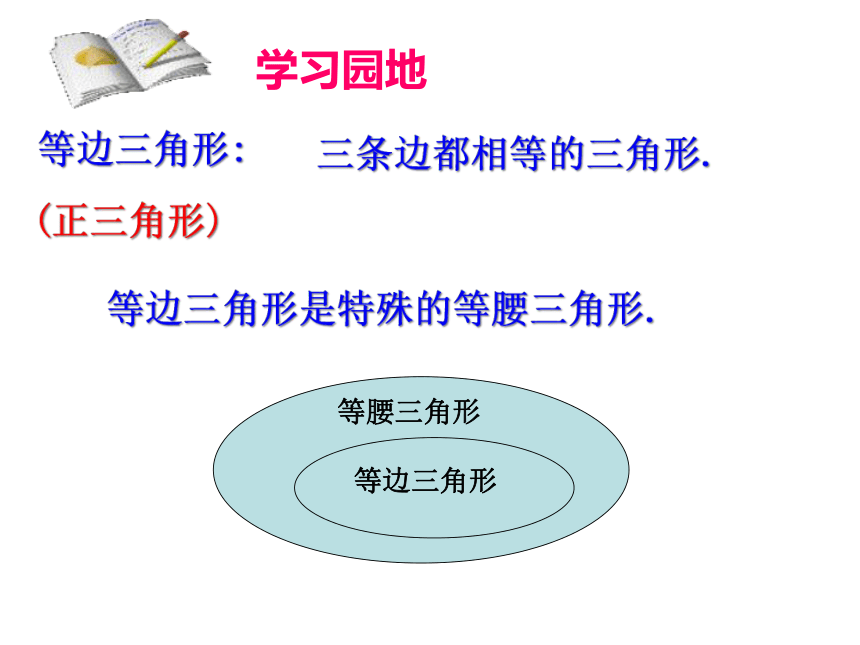
等边三角形:
(正三角形)
三条边都相等的三角形.
等边三角形是特殊的等腰三角形.
学习园地
等腰三角形
等边三角形
A
B
C
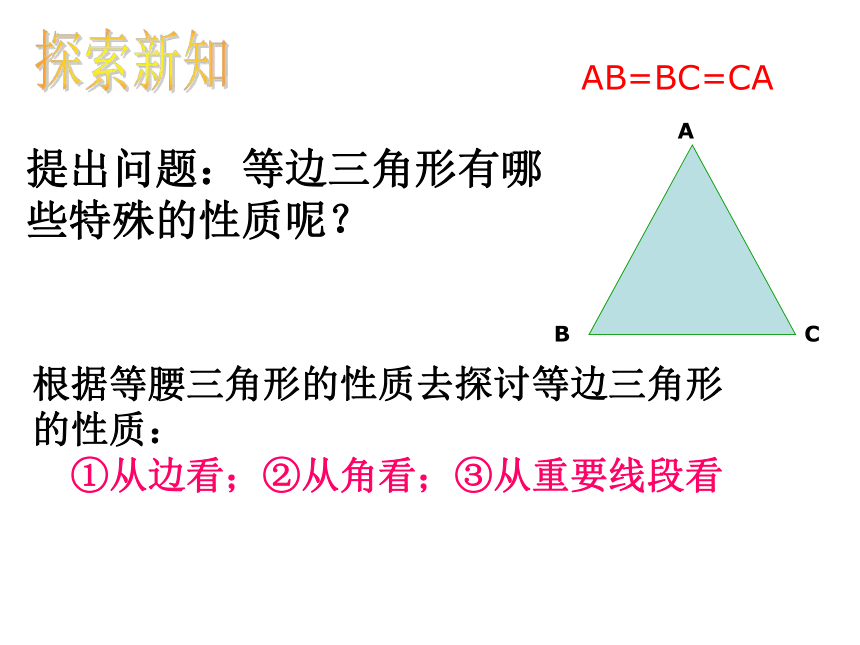
AB=BC=CA
提出问题:等边三角形有哪些特殊的性质呢?
根据等腰三角形的性质去探讨等边三角形的性质:
①从边看;②从角看;③从重要线段看
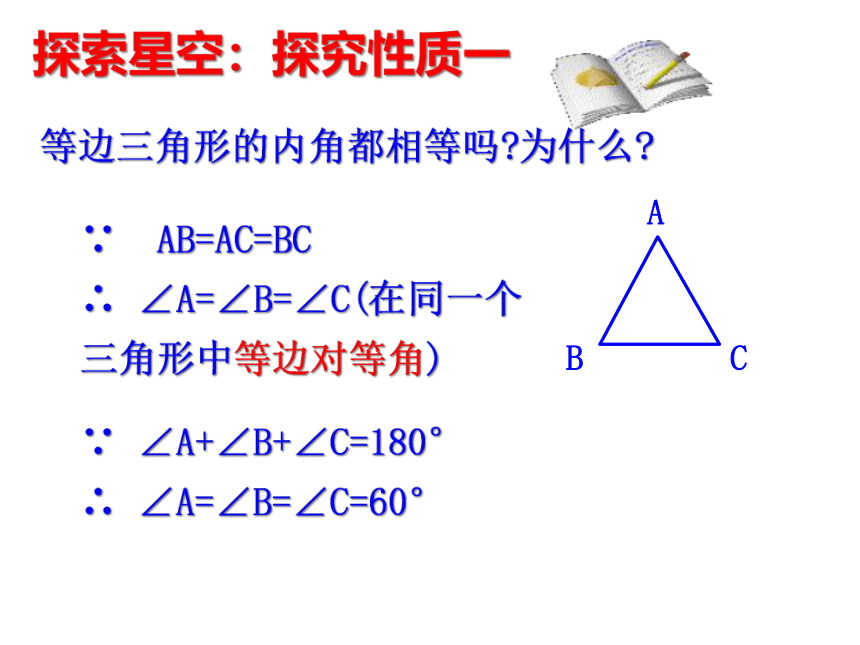
等边三角形的内角都相等吗?为什么?
∵ AB=AC=BC
∴ ∠A=∠B=∠C(在同一个三角形中等边对等角)
∵ ∠A+∠B+∠C=180°
∴ ∠A=∠B=∠C=60°
探索星空:探究性质一
探索结论:
2.等边三角形的三个内角都相等,并且每一个内角等于60 °。
等边三角形性质定理
1 .等边三角形的三条边都相等。
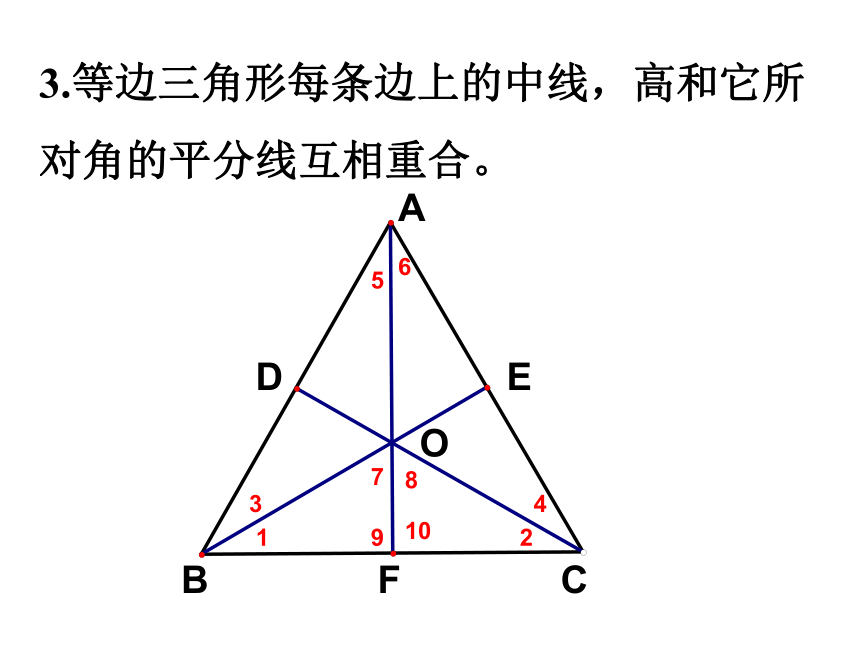
3.等边三角形每条边上的中线,高和它所对角的平分线互相重合。
A
F
E
D
C
B
O
6
5
4
3
2
1
8
10
9
7
等边三角形的性质
4.等边三角形是轴对称图形,有三条对称轴.
1 .等边三角形的三条边都相等。
2.等边三角形的三个内角都相等,并且每一个内角等于60 °。
3.等边三角形每条边上的中线,高和它所对角的平分线互相重合。(九线合三)
*
A
B
C
怎样判断三角形ABC是等边三角形?
方法一:三角形的三边考虑;
方法三:有一个角等于60°的等腰三角形是等边三角形。
方法二:三角形的三角考虑;
你能说明理由吗?
例:如图,△ABC是等边三角形,DE∥BC,分别交边AB、AC于点D,E.
求证:△ADE是等边三角形.
拓展: 如图,D、E、F分别是等边三角形ABC三边上三点,且AD=BE=CF。试问:△DEF是什么三角形?
检测
1、已知△ABC中,∠A=∠B=60°,AB=3cm ,则△ABC的周长________
2、 △ABC是等腰三角形,周长为15cm且∠A=60°,则BC=_______
3、如图,已知,△ABC是等边三角形,BD是中线,BD=6,延长BC到E,使CE=CD,求DE长.
A
B
C
D
E
4.已知:如图,P、Q是△ABC的边BC上
的两点,并PB=PQ=QC=AP=AQ,
求∠BAC的大小.
请你说一说这节课的收获和体验让大家与你一起分享 ?
等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗?
定义
性质
判定
等 腰
三 角 形
等 边
三 角 形
有两条边相等
1、两边、两角相等
2、三线合一
3、一条对称轴
1、三边、三角相等
2、三线合一
3、轴对称图形、三条对称轴
有三条边相等
1、定义
2、等角对等边
1、定义
2、三个角都相等
3、等腰三角形有一
个角是600
1.三边都相等的三角形叫做____三角形.
2.等边三角形的每个内角都等于____度.
3.等边三角形有____条对称轴.
等边
60
3
4、已知△ABC中,∠A=∠B=60°,AB=3cm 则△ABC的周长________
5、 △ABC是等腰三角形,周长为15cm且∠A=60°,则BC=_______
9
5
1、下列四个说法中,不正确的有( )
(A)0个(B)1个(C)2个(D)3个
三个角都相等的三角形是等边三角形。
有两个角等于60°的三角形是等边三角形。
有一个是60°的等腰三角形是等边三角形。
有两个角相等的等腰三角形是等边三角形。
2、等边三角形的对称轴有( )
(A)1条(B)2条(C)3条(D)4条
3、等边三角形中,高、中线、角平分线共有( )
(A)3条(B)6条(C)9条(D)7条
(选择)
B
C
A
在△ABC中,AB=AC,以AB、AC为边在△ABC的外侧作两个等边三角形△ABE和△ACD,且∠EDC=40°,则∠ABC=( )度?
名称
图 形
性 质
判 定
等
腰
三
角
形
A
B
C
等边对等角
三线合一
等角对等边
两边相等
两腰相等
轴对称图形
知识回顾
等边三角形:
(正三角形)
三条边都相等的三角形.
等边三角形是特殊的等腰三角形.
学习园地
等腰三角形
等边三角形
A
B
C
AB=BC=CA
提出问题:等边三角形有哪些特殊的性质呢?
根据等腰三角形的性质去探讨等边三角形的性质:
①从边看;②从角看;③从重要线段看
等边三角形的内角都相等吗?为什么?
∵ AB=AC=BC
∴ ∠A=∠B=∠C(在同一个三角形中等边对等角)
∵ ∠A+∠B+∠C=180°
∴ ∠A=∠B=∠C=60°
探索星空:探究性质一
探索结论:
2.等边三角形的三个内角都相等,并且每一个内角等于60 °。
等边三角形性质定理
1 .等边三角形的三条边都相等。
3.等边三角形每条边上的中线,高和它所对角的平分线互相重合。
A
F
E
D
C
B
O
6
5
4
3
2
1
8
10
9
7
等边三角形的性质
4.等边三角形是轴对称图形,有三条对称轴.
1 .等边三角形的三条边都相等。
2.等边三角形的三个内角都相等,并且每一个内角等于60 °。
3.等边三角形每条边上的中线,高和它所对角的平分线互相重合。(九线合三)
*
A
B
C
怎样判断三角形ABC是等边三角形?
方法一:三角形的三边考虑;
方法三:有一个角等于60°的等腰三角形是等边三角形。
方法二:三角形的三角考虑;
你能说明理由吗?
例:如图,△ABC是等边三角形,DE∥BC,分别交边AB、AC于点D,E.
求证:△ADE是等边三角形.
拓展: 如图,D、E、F分别是等边三角形ABC三边上三点,且AD=BE=CF。试问:△DEF是什么三角形?
检测
1、已知△ABC中,∠A=∠B=60°,AB=3cm ,则△ABC的周长________
2、 △ABC是等腰三角形,周长为15cm且∠A=60°,则BC=_______
3、如图,已知,△ABC是等边三角形,BD是中线,BD=6,延长BC到E,使CE=CD,求DE长.
A
B
C
D
E
4.已知:如图,P、Q是△ABC的边BC上
的两点,并PB=PQ=QC=AP=AQ,
求∠BAC的大小.
请你说一说这节课的收获和体验让大家与你一起分享 ?
等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗?
定义
性质
判定
等 腰
三 角 形
等 边
三 角 形
有两条边相等
1、两边、两角相等
2、三线合一
3、一条对称轴
1、三边、三角相等
2、三线合一
3、轴对称图形、三条对称轴
有三条边相等
1、定义
2、等角对等边
1、定义
2、三个角都相等
3、等腰三角形有一
个角是600
1.三边都相等的三角形叫做____三角形.
2.等边三角形的每个内角都等于____度.
3.等边三角形有____条对称轴.
等边
60
3
4、已知△ABC中,∠A=∠B=60°,AB=3cm 则△ABC的周长________
5、 △ABC是等腰三角形,周长为15cm且∠A=60°,则BC=_______
9
5
1、下列四个说法中,不正确的有( )
(A)0个(B)1个(C)2个(D)3个
三个角都相等的三角形是等边三角形。
有两个角等于60°的三角形是等边三角形。
有一个是60°的等腰三角形是等边三角形。
有两个角相等的等腰三角形是等边三角形。
2、等边三角形的对称轴有( )
(A)1条(B)2条(C)3条(D)4条
3、等边三角形中,高、中线、角平分线共有( )
(A)3条(B)6条(C)9条(D)7条
(选择)
B
C
A
在△ABC中,AB=AC,以AB、AC为边在△ABC的外侧作两个等边三角形△ABE和△ACD,且∠EDC=40°,则∠ABC=( )度?
