人教版八年级数学上册 第十五章 分式 15.1.2 分式的基本性质(第二课时)课件(共30张ppt)
文档属性
| 名称 | 人教版八年级数学上册 第十五章 分式 15.1.2 分式的基本性质(第二课时)课件(共30张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 09:31:36 | ||
图片预览









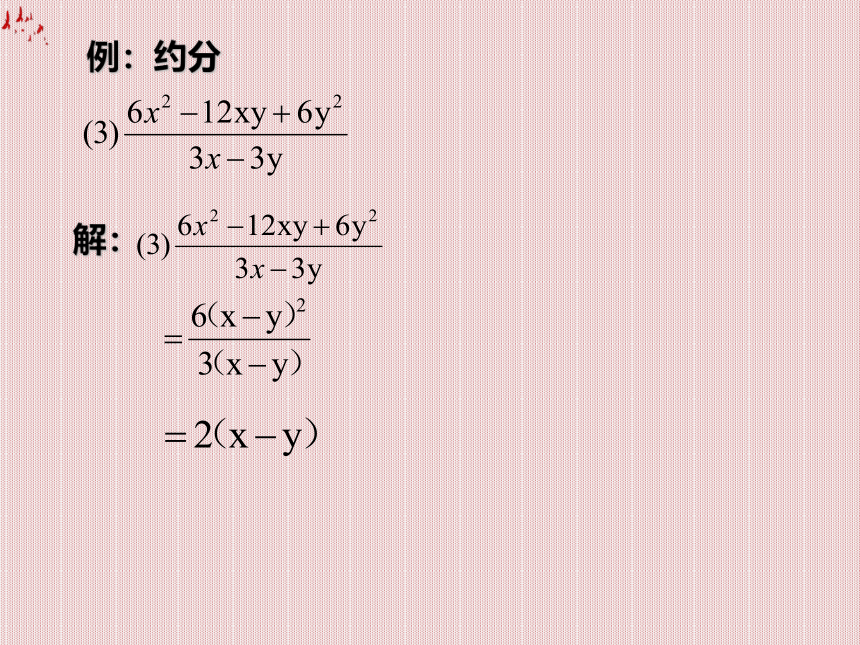


文档简介
第十五章 分式
15.1.2 分式的基本性质
第二课时
【学习目标】
1、理解并掌握分式的基本性质;
2、能运用分式基本性质进行分式的约分.
3、经历用类比、观察、联想的方法探索分式通分的方法的过程,理解通分与最简公分母的意义.
4、能正确熟练地运用分式的基本性质将分式通分.
【课前预习】
1.下列运算正确的是( )
A. B. C. D.
2.如果把分式 中的x和y的值都变为原来的2倍,那么分式的值( )
A.变为原来的2倍 B.变为原来的4倍 C.缩小为原来的 D.不变
3.化简 的结果是( )
A. B. C. D.
4.下列各式中,正确的是( )
5.下列运算中正确的是( )
【课前预习】答案
1.D
2.A
3.B
4.B
5.C
分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变。
用式子表示为:
其中A,B,C是整式。
分式的基本性质
复习回顾
分数是如何约分的?
1、约分:
约去分子与分母的最大公约数,化为最简分数。
=
复习回顾
这一过程实际上是将分式中分子与分母的公因式约去。
把分式分子、分母的公因式约去,这种变形叫分式的约分.
分式约分的依据是什么?
分式的基本性质
观察下列化简过程,你能发现什么?
分析:为约分要先找出分子和分母的公因式。
解:
找公因式方法
(1)约去系数的最大公约数
(2)约去分子分母相同因式的最低次幂
{
例:约分
例:约分
分析:为约分要先找出分子和分母的公因式。
解:
约分时,分子或分母若是多项式,能分解则必须先进行因式分解.再找出分子和分母的公因式进行约分
例:约分
解:
对于分数而言,彻底约分后的分数叫什么?
彻底约分后的分式叫最简分式.
一般约分要彻底, 使分子、分母没有公因式.
做一做
(1)
(2)
(3)
(4)
注意:
当分子分母是多项式的时候,先进行分解因式,再约分
(3)
(4)
练一练
计算:
分数的通分:
把几个异分母的分数化成同分母的分数,而不改变分数的值,叫做分数的通分。
通分的关键是确定几个分数的
各分母的最小公倍数12
和分数通分类似,把几个异分母的分式化成与原来的分式相等的同分母的分式叫做分式的通分。
最小公倍数。
(1)求分式
的最简公分母。
12
系数:各分母系数的最小公倍数。
因式:各分母所有因式的最高次幂。
三个分式的最简公分母为12x3y4z。
议一议
42x?
尝试练习一:
通分
2、试确定下列分式的最简公分母:
最简公分母是:xy(x-y)2(x+y)
(分母中虽然有的因式是多项式,但仍然是积的形式。)
3、求分式
与
的最简公分母。
把这两个分式的分母中所有的因式都取到,其中,系数取正数,取它们的积,即 就是这两个分式的最简公分母。
若分母是多项式时,应先将各分母分解因式,再找出最简公分母。
确定几个分式的最简公分母的方法:
(1)系数:分式分母系数的最小公倍数;
(2)因式:凡各分母中出现的不同因式都
要取到;
(3)因式的指数:相同因式取指数最高的。
归纳:
例 通分
(1)
(2)
与
与
解:
(1)最简公分母是
(3)
(2)
与
解:
(2)最简公分母是
(3)
解:
(3)最简公分母是
把一个分式的分子和分母的公因式约去,不改变分式的值,这种变形叫做分式的约分。
1.约分的依据是:
分式的基本性质
2.约分的基本方法是:
先找出分式的分子、分母公因式,再约去公因式.
3.约分的结果是:
整式或最简分式
小结
4、分式的通分与分数的通分类似,正确掌握分式通分的方法和步骤,才能熟练地进行以后分式的加减法运算;
5、通分的关键是确定最简公分母,包括系数、因式和因式的指数;分母是多项式的要先分解因式;
6、分式通分的依据是分式的基本性质,每一步变形综合性都较强,计算时要步步细心;
7、分式通分的基本步骤:
(1)、将各分母分解因式
(2)、寻找最简公分母(方法要记牢)
(3)、根据分式的基本性质,把各分式的分子分母乘以同一个整式,化异分母为最简公分母。(分子运算很重要)
(1)将各个分式的分母分解因式;(2)取各分母系数的最小公倍数(3)凡是出现的所有字母或因式都要取;(4)相同字母(或含字母的式子)的幂取指数最大的;(5)将上述所得系数的最小公倍数与各字母(或因式)的最高次幂全都乘起来,就得到了最简公分母
【课后练习】
【课后练习】答案
1.A 2.C 3.B 4.C 5.D 6.B 7.C 8.B 9.C 10.B
11.1
12.6x?y?
13.a2-b2≠0
14. x≠-2 x=-3 x?-x
15.x(x+2)(x-2)
15.1.2 分式的基本性质
第二课时
【学习目标】
1、理解并掌握分式的基本性质;
2、能运用分式基本性质进行分式的约分.
3、经历用类比、观察、联想的方法探索分式通分的方法的过程,理解通分与最简公分母的意义.
4、能正确熟练地运用分式的基本性质将分式通分.
【课前预习】
1.下列运算正确的是( )
A. B. C. D.
2.如果把分式 中的x和y的值都变为原来的2倍,那么分式的值( )
A.变为原来的2倍 B.变为原来的4倍 C.缩小为原来的 D.不变
3.化简 的结果是( )
A. B. C. D.
4.下列各式中,正确的是( )
5.下列运算中正确的是( )
【课前预习】答案
1.D
2.A
3.B
4.B
5.C
分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变。
用式子表示为:
其中A,B,C是整式。
分式的基本性质
复习回顾
分数是如何约分的?
1、约分:
约去分子与分母的最大公约数,化为最简分数。
=
复习回顾
这一过程实际上是将分式中分子与分母的公因式约去。
把分式分子、分母的公因式约去,这种变形叫分式的约分.
分式约分的依据是什么?
分式的基本性质
观察下列化简过程,你能发现什么?
分析:为约分要先找出分子和分母的公因式。
解:
找公因式方法
(1)约去系数的最大公约数
(2)约去分子分母相同因式的最低次幂
{
例:约分
例:约分
分析:为约分要先找出分子和分母的公因式。
解:
约分时,分子或分母若是多项式,能分解则必须先进行因式分解.再找出分子和分母的公因式进行约分
例:约分
解:
对于分数而言,彻底约分后的分数叫什么?
彻底约分后的分式叫最简分式.
一般约分要彻底, 使分子、分母没有公因式.
做一做
(1)
(2)
(3)
(4)
注意:
当分子分母是多项式的时候,先进行分解因式,再约分
(3)
(4)
练一练
计算:
分数的通分:
把几个异分母的分数化成同分母的分数,而不改变分数的值,叫做分数的通分。
通分的关键是确定几个分数的
各分母的最小公倍数12
和分数通分类似,把几个异分母的分式化成与原来的分式相等的同分母的分式叫做分式的通分。
最小公倍数。
(1)求分式
的最简公分母。
12
系数:各分母系数的最小公倍数。
因式:各分母所有因式的最高次幂。
三个分式的最简公分母为12x3y4z。
议一议
42x?
尝试练习一:
通分
2、试确定下列分式的最简公分母:
最简公分母是:xy(x-y)2(x+y)
(分母中虽然有的因式是多项式,但仍然是积的形式。)
3、求分式
与
的最简公分母。
把这两个分式的分母中所有的因式都取到,其中,系数取正数,取它们的积,即 就是这两个分式的最简公分母。
若分母是多项式时,应先将各分母分解因式,再找出最简公分母。
确定几个分式的最简公分母的方法:
(1)系数:分式分母系数的最小公倍数;
(2)因式:凡各分母中出现的不同因式都
要取到;
(3)因式的指数:相同因式取指数最高的。
归纳:
例 通分
(1)
(2)
与
与
解:
(1)最简公分母是
(3)
(2)
与
解:
(2)最简公分母是
(3)
解:
(3)最简公分母是
把一个分式的分子和分母的公因式约去,不改变分式的值,这种变形叫做分式的约分。
1.约分的依据是:
分式的基本性质
2.约分的基本方法是:
先找出分式的分子、分母公因式,再约去公因式.
3.约分的结果是:
整式或最简分式
小结
4、分式的通分与分数的通分类似,正确掌握分式通分的方法和步骤,才能熟练地进行以后分式的加减法运算;
5、通分的关键是确定最简公分母,包括系数、因式和因式的指数;分母是多项式的要先分解因式;
6、分式通分的依据是分式的基本性质,每一步变形综合性都较强,计算时要步步细心;
7、分式通分的基本步骤:
(1)、将各分母分解因式
(2)、寻找最简公分母(方法要记牢)
(3)、根据分式的基本性质,把各分式的分子分母乘以同一个整式,化异分母为最简公分母。(分子运算很重要)
(1)将各个分式的分母分解因式;(2)取各分母系数的最小公倍数(3)凡是出现的所有字母或因式都要取;(4)相同字母(或含字母的式子)的幂取指数最大的;(5)将上述所得系数的最小公倍数与各字母(或因式)的最高次幂全都乘起来,就得到了最简公分母
【课后练习】
【课后练习】答案
1.A 2.C 3.B 4.C 5.D 6.B 7.C 8.B 9.C 10.B
11.1
12.6x?y?
13.a2-b2≠0
14. x≠-2 x=-3 x?-x
15.x(x+2)(x-2)
