人教版八年级数学上册教学课件14.1.4整式的乘法 第三课时多项式与多项式相乘(共16张ppt)
文档属性
| 名称 | 人教版八年级数学上册教学课件14.1.4整式的乘法 第三课时多项式与多项式相乘(共16张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览




文档简介
新疆教科研
微信公众号
第十四章 整式的乘法与因式分解
14.1.4整式的乘法
第三课时多项式与多项式相乘
人教版八年级上册
学习目标
1、通过经历探索多项式乘法法则的过程,让学生理解多项式乘法法则。
2、通过运用多乘多运算法则;学生能学会运算,体会乘法分配律的作用与转化思想,发展有条理的思考及逻辑推理能力。
复习巩固
1、前几节课,我们学习了整式的哪些相关运算?
单项式乘以多项式的法则:单项式与多项式相乘,
就是用单项式去乘多项式的每一项,再把所得的积相加。
单项式乘以单项式的法则:单项式与单项式相乘,
将系数与同底数幂分别相乘,对于单独出现的字母,则连同它的指数作为积的一个因式。
推进新课
多项式乘多项式的运算法则
探究1
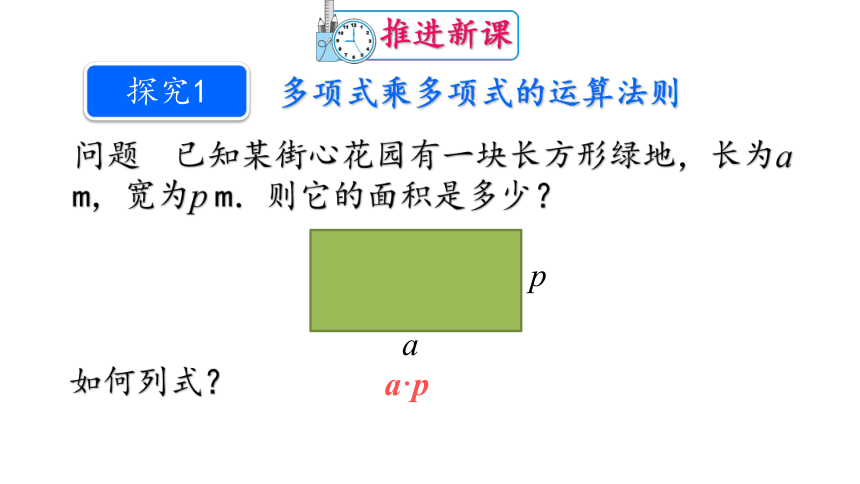
问题 已知某街心花园有一块长方形绿地,长为a m,宽为p m.则它的面积是多少?
如何列式?
a·p
a
p
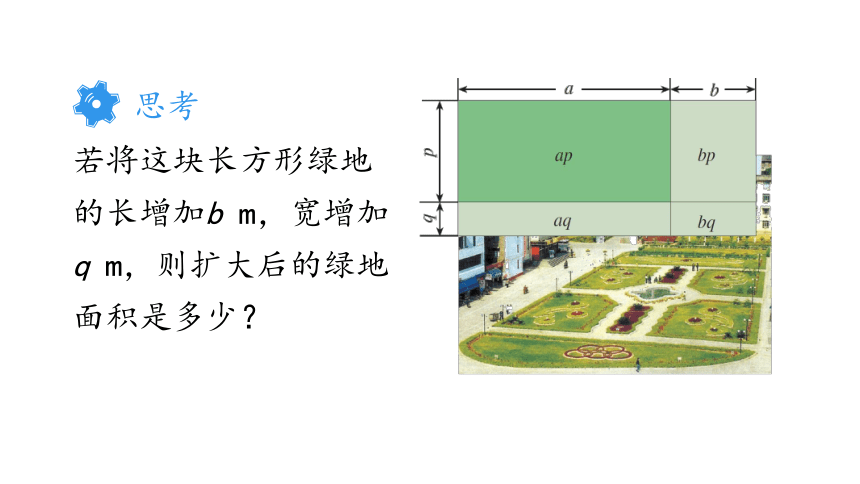
若将这块长方形绿地的长增加b m,宽增加q m,则扩大后的绿地面积是多少?
思考
a+b
p+q
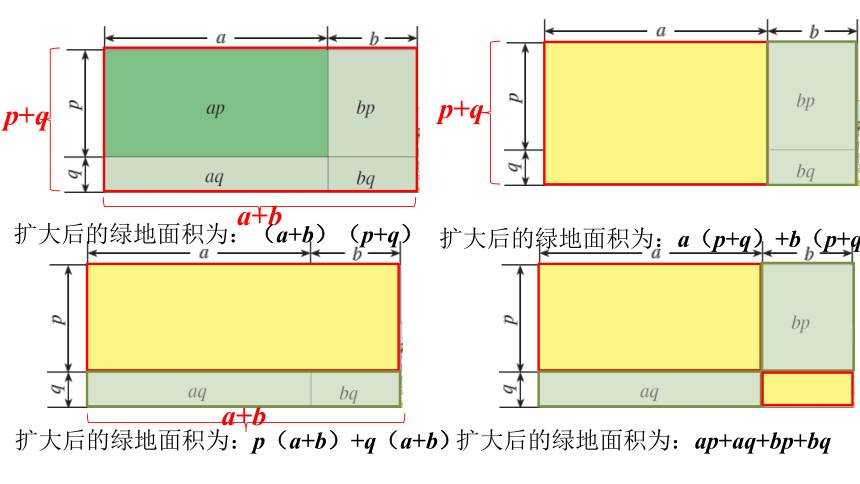
扩大后的绿地面积为:(a+b)(p+q)
p+q
扩大后的绿地面积为:a(p+q)+b(p+q)
a+b
扩大后的绿地面积为:p(a+b)+q(a+b)
扩大后的绿地面积为:ap+aq+bp+bq
根据上节课积累的探究经验,你能得出什么结论呢?
不同的表示方法:
(a+b)(p+q)
a(p+q)+b(p+q)
p(a+b)+q(a+b)
ap+aq+bp+bq
多项式乘多项式
单项式乘多项式
单项式乘单项式
多项式的乘法法则
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加。
=
ap
2
3
4
+aq
+bp
(a+b)(p+q)
+bq
2
3
4
1
1
多项式的乘法法则几何语言
(1)(3x+1)(x+2)
解原式= 3x · x+3x · 2+1 · x+1×2
= 3x2+6x+x+2
= 3x2+7x+2.
例1:计算:(教材101页例6)
(1)(3x+1)(x+2); (2)(x- 8y )(x-y );
(3)(x+y )(x 2 -xy+y 2).
(2) (x-8y )(x-y )
解原式=x · x+x · (-y)+(-8y) · x+(-8y) · (-y)
=x 2-xy-8xy+8y 2
=x 2-9xy+8y 2 .
(3)(x+y)(x 2 -xy+y 2)
解原式=x·x 2+x(-xy)+xy 2+x 2y-xy·y+y·y 2
=x 3-x 2y+xy 2+x 2y-xy 2 +y 3
=x 3 +y 3.
探究2
法则运用
随堂演练
1.计算
(1) (2x+1)(x+3) (2) (m+2n)(m+3n)
(3) (a-1)2 (4) (a+3b)(a-3b)
(5) (y+4)(y-2) (6) (y-5)(y-3)
解原式
解原式
解原式
解原式
解原式
解原式
多项式与多项式相乘的法则:
运用多项式乘以多项式的法则时,应注意哪些问题呢?
(1)多项式与多项式相乘实质上是转化为单项式乘以单项式.
(2)用多项式去乘多项式中的每一项时,不能漏乘.
(3)多项式乘多项式,积的项数就是两个多项式的项数之积
(4)多项式中的每一项都包括它前面的符号.
(a+b)(p+q)=ap+aq+bp+bq
随堂演练
1.判断
(1)(1-x)(0.6-x);
(2)(2x+y)·(2x-y);
(3)(x-y)2;
(4)(2x2-1)(2x+3)
0.6-1.6x+x2
2x2-xy -y2
x2-2xy -y2
4x3+6x2-2x-3
√
√
×
×
课堂小结
1、这节课你学习了哪些内容?
2、多项式与多项式相乘的运算法则。
3、多项式与多项式相乘应该注意什么?
3.总结提升:
整式的乘法中我们学习了三个运算法则,它们都是由乘法的运算律推理出来的
在这三个法则中,单项式乘单项式的法则是基础,是关键。
p(a+b+c)=pa+pb+pc.
(a+b)(p+q)=ap+aq+bp+bq
课后作业
1、书102页的练习1,2
2、预习同底数幂的除法
3、开动脑筋:多个多项式怎样相乘呢?
(a+b)(p+q)(m+n)=?
(1) (x+2)(x+3) (2)(x-4)(x+1)
(3)(y+4)(y-2) (4)(y-5)(y-3)
由上面的结果找规律,观察右图,填空:
探究3
多乘多的特殊形式
x与p的和,与x与q的和相乘
将p和q的乘积作为常数项;
将p与q的和作为一次项系数;
二次项的系数为一。
微信公众号
第十四章 整式的乘法与因式分解
14.1.4整式的乘法
第三课时多项式与多项式相乘
人教版八年级上册
学习目标
1、通过经历探索多项式乘法法则的过程,让学生理解多项式乘法法则。
2、通过运用多乘多运算法则;学生能学会运算,体会乘法分配律的作用与转化思想,发展有条理的思考及逻辑推理能力。
复习巩固
1、前几节课,我们学习了整式的哪些相关运算?
单项式乘以多项式的法则:单项式与多项式相乘,
就是用单项式去乘多项式的每一项,再把所得的积相加。
单项式乘以单项式的法则:单项式与单项式相乘,
将系数与同底数幂分别相乘,对于单独出现的字母,则连同它的指数作为积的一个因式。
推进新课
多项式乘多项式的运算法则
探究1
问题 已知某街心花园有一块长方形绿地,长为a m,宽为p m.则它的面积是多少?
如何列式?
a·p
a
p
若将这块长方形绿地的长增加b m,宽增加q m,则扩大后的绿地面积是多少?
思考
a+b
p+q
扩大后的绿地面积为:(a+b)(p+q)
p+q
扩大后的绿地面积为:a(p+q)+b(p+q)
a+b
扩大后的绿地面积为:p(a+b)+q(a+b)
扩大后的绿地面积为:ap+aq+bp+bq
根据上节课积累的探究经验,你能得出什么结论呢?
不同的表示方法:
(a+b)(p+q)
a(p+q)+b(p+q)
p(a+b)+q(a+b)
ap+aq+bp+bq
多项式乘多项式
单项式乘多项式
单项式乘单项式
多项式的乘法法则
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加。
=
ap
2
3
4
+aq
+bp
(a+b)(p+q)
+bq
2
3
4
1
1
多项式的乘法法则几何语言
(1)(3x+1)(x+2)
解原式= 3x · x+3x · 2+1 · x+1×2
= 3x2+6x+x+2
= 3x2+7x+2.
例1:计算:(教材101页例6)
(1)(3x+1)(x+2); (2)(x- 8y )(x-y );
(3)(x+y )(x 2 -xy+y 2).
(2) (x-8y )(x-y )
解原式=x · x+x · (-y)+(-8y) · x+(-8y) · (-y)
=x 2-xy-8xy+8y 2
=x 2-9xy+8y 2 .
(3)(x+y)(x 2 -xy+y 2)
解原式=x·x 2+x(-xy)+xy 2+x 2y-xy·y+y·y 2
=x 3-x 2y+xy 2+x 2y-xy 2 +y 3
=x 3 +y 3.
探究2
法则运用
随堂演练
1.计算
(1) (2x+1)(x+3) (2) (m+2n)(m+3n)
(3) (a-1)2 (4) (a+3b)(a-3b)
(5) (y+4)(y-2) (6) (y-5)(y-3)
解原式
解原式
解原式
解原式
解原式
解原式
多项式与多项式相乘的法则:
运用多项式乘以多项式的法则时,应注意哪些问题呢?
(1)多项式与多项式相乘实质上是转化为单项式乘以单项式.
(2)用多项式去乘多项式中的每一项时,不能漏乘.
(3)多项式乘多项式,积的项数就是两个多项式的项数之积
(4)多项式中的每一项都包括它前面的符号.
(a+b)(p+q)=ap+aq+bp+bq
随堂演练
1.判断
(1)(1-x)(0.6-x);
(2)(2x+y)·(2x-y);
(3)(x-y)2;
(4)(2x2-1)(2x+3)
0.6-1.6x+x2
2x2-xy -y2
x2-2xy -y2
4x3+6x2-2x-3
√
√
×
×
课堂小结
1、这节课你学习了哪些内容?
2、多项式与多项式相乘的运算法则。
3、多项式与多项式相乘应该注意什么?
3.总结提升:
整式的乘法中我们学习了三个运算法则,它们都是由乘法的运算律推理出来的
在这三个法则中,单项式乘单项式的法则是基础,是关键。
p(a+b+c)=pa+pb+pc.
(a+b)(p+q)=ap+aq+bp+bq
课后作业
1、书102页的练习1,2
2、预习同底数幂的除法
3、开动脑筋:多个多项式怎样相乘呢?
(a+b)(p+q)(m+n)=?
(1) (x+2)(x+3) (2)(x-4)(x+1)
(3)(y+4)(y-2) (4)(y-5)(y-3)
由上面的结果找规律,观察右图,填空:
探究3
多乘多的特殊形式
x与p的和,与x与q的和相乘
将p和q的乘积作为常数项;
将p与q的和作为一次项系数;
二次项的系数为一。
