人教版九年级上册数学课件:24.1.2 垂径垂径定理(共32张ppt)
文档属性
| 名称 | 人教版九年级上册数学课件:24.1.2 垂径垂径定理(共32张ppt) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 09:35:51 | ||
图片预览








文档简介
温固而知新
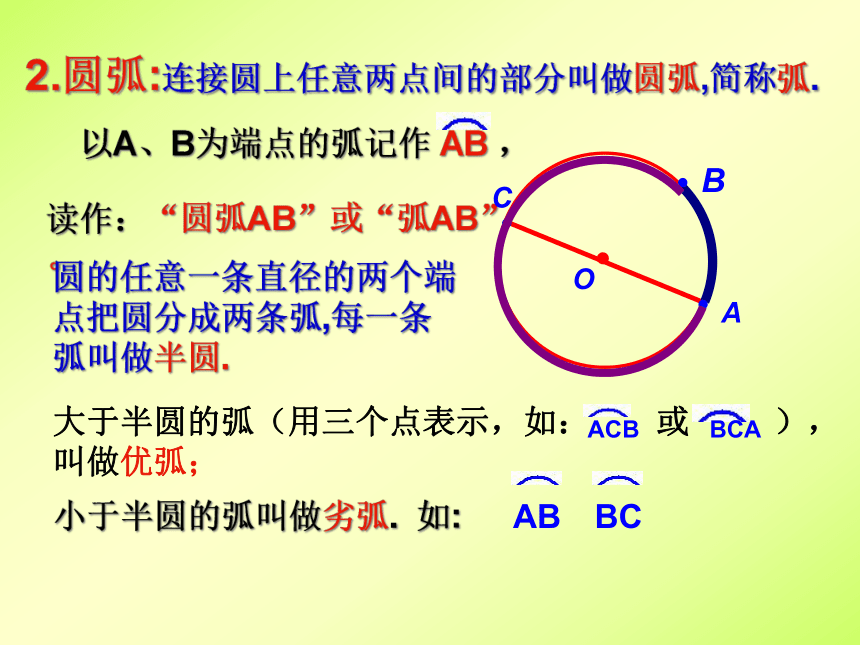
一、圆的定义:
平面上到定点的距离等于定长的所有点组成的图形叫做圆.
二、圆的相关概念
1、连接圆上任意两点间
的线段叫做弦(如弦AB).
经过圆心的弦叫做直径
(如直径AC).
.
O
A
B
C
弦
直径
2.圆弧:连接圆上任意两点间的部分叫做圆弧,简称弧.
以A、B为端点的弧记作 AB ,
读作:“圆弧AB”或“弧AB”。
大于半圆的弧(用三个点表示,如: 或 ),
叫做优弧;
小于半圆的弧叫做劣弧. 如:
C
B
A
O
ACB
BCA
BC
AB
圆的任意一条直径的两个端
点把圆分成两条弧,每一条
弧叫做半圆.
M
●O
A
B
C
注意:
直径是弦,但弦不一定是直径;
半圆是弧,但弧不一定是半圆;
半圆既不是劣弧,也不是优弧
3、等圆:能够重合的两个圆叫做等圆,半径相等的两个圆也是等圆;反过来,同圆或等圆的半径相等。
4、等弧:在同圆或等圆中,能够互相重合的弧。
5、同心圆:圆心相同,半径不相等的两个圆.
6、弓形:由弦及其所对的弧组成的图形
叫做弓形.
圆对称性(1)
--垂径定理
问题 :你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗?
赵州桥主桥拱的半径是多少?
●O
1)圆是轴对称图形吗?如果是,你能找到多少条对称轴?它的对称轴是什么?
圆是轴对称图形,它有无数条对称轴,
它的对称轴是任意一条经过圆心的直线.
探究:
此外,圆还是中心对称图形,对称中心是圆心。
圆绕圆心旋转任意角度后都与
自身重合,所以圆具有旋转不
变性。
(2)你能发现图中有哪些相等的线段和弧?为什么?
2、如图,AB是⊙O的一条弦.
作直径CD,使CD⊥AB,垂足为M.
(1)右图是轴对称图形吗?
●O
A
B
C
D
M└
图中有:
你是怎样知道?
⌒
⌒
AC = BC
⌒
⌒
AD =BD
AM=BM,
如果是,其对称轴是什么?
探究:
叠合法
·
O
A
B
C
D
E
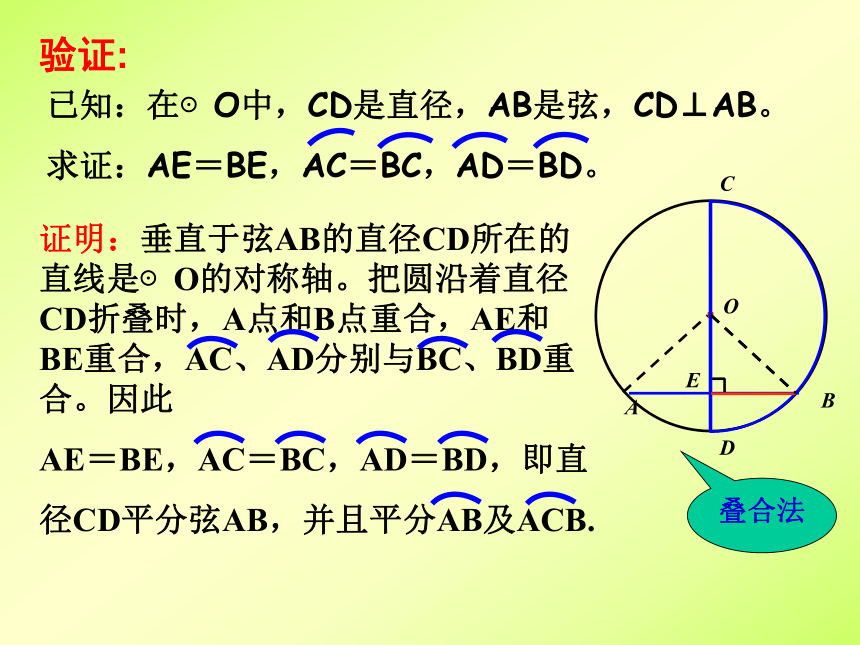
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB。
求证:AE=BE,AC=BC,AD=BD。
证明:垂直于弦AB的直径CD所在的直线是⊙O的对称轴。把圆沿着直径CD折叠时,A点和B点重合,AE和BE重合,AC、AD分别与BC、BD重合。因此
AE=BE,AC=BC,AD=BD,即直
径CD平分弦AB,并且平分AB及ACB.
验证:
结论:
AC=BC
AD=BD,
∴AM=BM
垂直于弦的直径, 平分这条弦, 并且平分弦所对的两条弧。
B
M
O
A
C
D
(垂径定理)
垂径定理是圆中一个重要的结论,是计算线段长度的重要根据.
两个条件:直径,垂直于弦.缺一不可!
∵CD是直径,CD⊥AB于M点
应用格式:
连接OA、OB,
则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM(HL).
∴AM=BM.
●O
A
B
C
D
M└
∵CD⊥AB
∴∠OMA=∠OMB=90°
也可利用等腰三角形三线合一性质
★试证明: AM=BM.
●O
A
B
C
D
M└
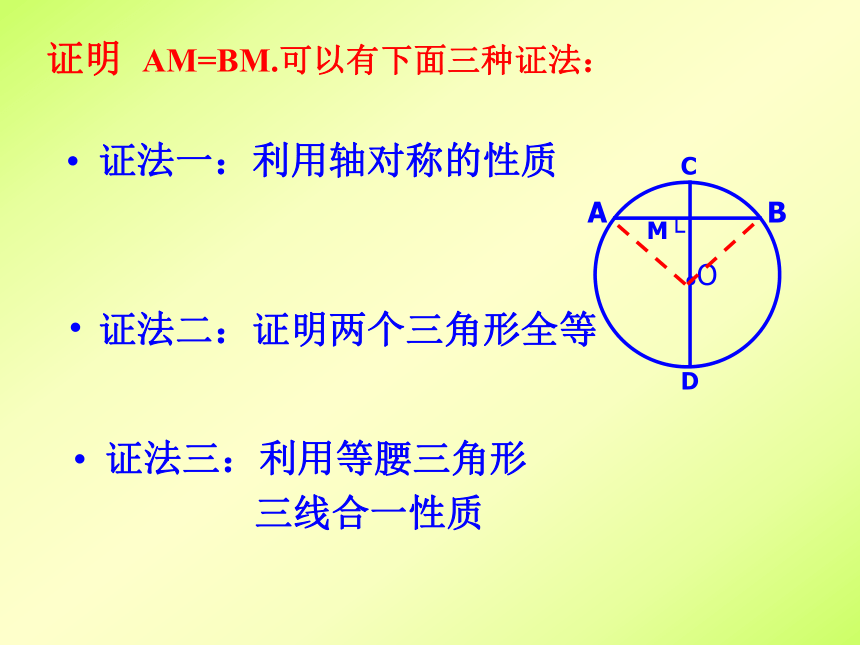
证法一:利用轴对称的性质
证法二:证明两个三角形全等
证法三:利用等腰三角形
三线合一性质
证明 AM=BM.可以有下面三种证法:
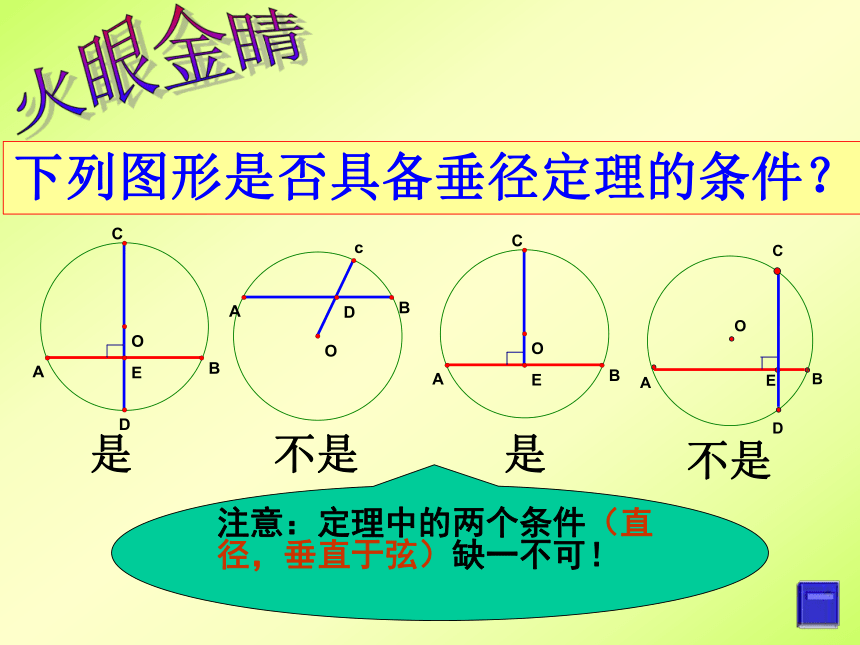
下列图形是否具备垂径定理的条件?
是
不是
是
不是
O
E
D
C
A
B
注意:定理中的两个条件(直径,垂直于弦)缺一不可!
挑战自我找一找
已知:如图,⊙O 中,弦AB∥CD,AB<CD,
直径MN⊥AB,垂足为E,交弦CD于点F.
图中相等的线段有 :
.
图中相等的劣弧有:
.
M
N
A
B
C
D
E
F
O
●
1、如图,AB是圆的弦,利用一个三角板,你能确定这条弦的中点吗?
2、如图,点C是圆的任意一个点,利用一个三角板,你能画出一条弦AB,使点C刚好是这条弦的中点吗?
●
C
A
B
O
O
1.在⊙O中,若CD ⊥AB于M,AB为直径,则下列结论不正确的是( )
2.已知⊙O的直径AB=10,弦CD ⊥AB,垂足为M,OM=3,则CD= .
3.在⊙O中,CD ⊥AB于M,AB为直径,若CD=10,AM=1,则⊙O的半径是 .
●O
C
D
A
B
M└
C
A、AC=AD B、BC=BD
C、AM=OM D、CM=DM
⌒
⌒
⌒
⌒
8
13
注意:解决有关弦的问题时,半径是常用的一种辅助线的添法.往往结合勾股定理计算。
垂径定理的应用:
1、如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离(弦心距)为3厘米,求⊙O的半径。
.O
A
B
E
解:过O作OE⊥AB于E点.
连结OA,在RtAOE中,根据勾股定理:
∴⊙O的半径为5厘米。
练习:
2.在半径为30㎜的⊙O中,弦AB=36㎜,求O到AB的距离。
O
A
B
P
解:过O点作OP⊥AB,连OA.
在Rt⊿AOP中,根据勾股定理:
∴O到AB的距离为24mm。
3.已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。你认为AC和BD有什么关系?为什么?
过O作OE⊥AB,垂足为E,
则AE=BE,CE=DE.
∴ AE-CE=BE-DE
即 AC=BD
.
A
C
D
B
O
E
注意:解决有关弦的问题,过圆心作弦的垂线,也是一种常用辅助线的添法.
解: AC=BD,
理由是:
归纳:
1、解决有关弦的问题时,经常过圆心作弦的垂线、连结半径等辅助线,构成直角三角形。为利用垂径定理和勾股定理创造条件。
.
A
B
O
2、如果弦长为a,弦心距为d,半径为r,弓形的高为h.
⑴d + h = r
⑵
在a、d、r、h四个量中,已知其中任意两个量,可以求出其它两个量.
⑴d + h = r
⑵
1、已知:如图,直径CD⊥AB.
⑴若半径R = 2 ,AB = , 求OE、DE 的长.
⑵若半径R = 2 ,OE = 1 ,求AB、DE 的长.
试一试:
在a、d、r、h四个量中,已知其中任意两个量,可以求出其它两个量.
1、如图,AB为⊙O的直径,CD为弦,CD⊥AB于E.则下列结论中错误的是(??? ? ).
A.∠COE=∠DOE B.CE=DE
C.AE=OE D.BC= BD
c
2、如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM的长的最小值为____最大值为____.
3
5
练习:
3、如图,矩形ABCD与圆O交于点A、B、
E、F,DE=1cm,EF=3cm,则AB=_____cm
5
M
N
4、已知:如图,AB是⊙O直径,与CD相交于点E,已知AE=1cm,BE=5cm,∠DEB=600,求弦CD的长.
.O
C
D
A
B
E
解:连结OA、OB
则OA=OB
∴∠OAB=∠OBA
又∵AC=BD
△AOC≌△BOD(SAS)
5、如图,在圆O中,已知AC=BD,
试说明: OC=OD
∴OC=OD
问题 :你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗?
垂径定理的应用:
37.4m
7.2m
A
B
O
C
E
赵州石拱桥
解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
过圆心O作弦AB的垂线OD,与 相交于点C. CD就是拱高.
根据垂径定理得:AD=BD。
由题设
在Rt△OAD中,由勾股定理,得
解得 R≈27.9(m).
答:赵州石拱桥的桥拱半径约为27.9m.
R
D
37.4
7.2
垂径定理的应用
2、如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径.
解:连接OC.
●
O
C
D
E
F
┗
注意闪烁的三角形的特点.
小结:
解决有关弦的问题,经常是
过圆心作弦的垂线,
或作垂直于弦的直径,
连结半径等辅助线,
构成直角三角形,为应用垂径定理创造条件。
.
A
B
O
垂径定理
挑 战自我
1、要把实际问题转变成一个数学问题来解决.
2、熟练地运用垂径定理及其推论、勾股定理,并用方程的思想来解决问题.
3、对于一个圆中的弦长a、圆心到弦的距离d、圆半径r、弓形高h,这四个量中,只要已知其中任意两个量,就可以求出另外两个量,如图有:
⑴d + h = r
⑵
通过这节课的学习,
你有哪些收获?
能与大家一起分享吗?
丰 收 园
结束寄语
读书要从薄到厚,再从厚到薄.
下课了!
一、圆的定义:
平面上到定点的距离等于定长的所有点组成的图形叫做圆.
二、圆的相关概念
1、连接圆上任意两点间
的线段叫做弦(如弦AB).
经过圆心的弦叫做直径
(如直径AC).
.
O
A
B
C
弦
直径
2.圆弧:连接圆上任意两点间的部分叫做圆弧,简称弧.
以A、B为端点的弧记作 AB ,
读作:“圆弧AB”或“弧AB”。
大于半圆的弧(用三个点表示,如: 或 ),
叫做优弧;
小于半圆的弧叫做劣弧. 如:
C
B
A
O
ACB
BCA
BC
AB
圆的任意一条直径的两个端
点把圆分成两条弧,每一条
弧叫做半圆.
M
●O
A
B
C
注意:
直径是弦,但弦不一定是直径;
半圆是弧,但弧不一定是半圆;
半圆既不是劣弧,也不是优弧
3、等圆:能够重合的两个圆叫做等圆,半径相等的两个圆也是等圆;反过来,同圆或等圆的半径相等。
4、等弧:在同圆或等圆中,能够互相重合的弧。
5、同心圆:圆心相同,半径不相等的两个圆.
6、弓形:由弦及其所对的弧组成的图形
叫做弓形.
圆对称性(1)
--垂径定理
问题 :你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗?
赵州桥主桥拱的半径是多少?
●O
1)圆是轴对称图形吗?如果是,你能找到多少条对称轴?它的对称轴是什么?
圆是轴对称图形,它有无数条对称轴,
它的对称轴是任意一条经过圆心的直线.
探究:
此外,圆还是中心对称图形,对称中心是圆心。
圆绕圆心旋转任意角度后都与
自身重合,所以圆具有旋转不
变性。
(2)你能发现图中有哪些相等的线段和弧?为什么?
2、如图,AB是⊙O的一条弦.
作直径CD,使CD⊥AB,垂足为M.
(1)右图是轴对称图形吗?
●O
A
B
C
D
M└
图中有:
你是怎样知道?
⌒
⌒
AC = BC
⌒
⌒
AD =BD
AM=BM,
如果是,其对称轴是什么?
探究:
叠合法
·
O
A
B
C
D
E
已知:在⊙O中,CD是直径,AB是弦,CD⊥AB。
求证:AE=BE,AC=BC,AD=BD。
证明:垂直于弦AB的直径CD所在的直线是⊙O的对称轴。把圆沿着直径CD折叠时,A点和B点重合,AE和BE重合,AC、AD分别与BC、BD重合。因此
AE=BE,AC=BC,AD=BD,即直
径CD平分弦AB,并且平分AB及ACB.
验证:
结论:
AC=BC
AD=BD,
∴AM=BM
垂直于弦的直径, 平分这条弦, 并且平分弦所对的两条弧。
B
M
O
A
C
D
(垂径定理)
垂径定理是圆中一个重要的结论,是计算线段长度的重要根据.
两个条件:直径,垂直于弦.缺一不可!
∵CD是直径,CD⊥AB于M点
应用格式:
连接OA、OB,
则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM(HL).
∴AM=BM.
●O
A
B
C
D
M└
∵CD⊥AB
∴∠OMA=∠OMB=90°
也可利用等腰三角形三线合一性质
★试证明: AM=BM.
●O
A
B
C
D
M└
证法一:利用轴对称的性质
证法二:证明两个三角形全等
证法三:利用等腰三角形
三线合一性质
证明 AM=BM.可以有下面三种证法:
下列图形是否具备垂径定理的条件?
是
不是
是
不是
O
E
D
C
A
B
注意:定理中的两个条件(直径,垂直于弦)缺一不可!
挑战自我找一找
已知:如图,⊙O 中,弦AB∥CD,AB<CD,
直径MN⊥AB,垂足为E,交弦CD于点F.
图中相等的线段有 :
.
图中相等的劣弧有:
.
M
N
A
B
C
D
E
F
O
●
1、如图,AB是圆的弦,利用一个三角板,你能确定这条弦的中点吗?
2、如图,点C是圆的任意一个点,利用一个三角板,你能画出一条弦AB,使点C刚好是这条弦的中点吗?
●
C
A
B
O
O
1.在⊙O中,若CD ⊥AB于M,AB为直径,则下列结论不正确的是( )
2.已知⊙O的直径AB=10,弦CD ⊥AB,垂足为M,OM=3,则CD= .
3.在⊙O中,CD ⊥AB于M,AB为直径,若CD=10,AM=1,则⊙O的半径是 .
●O
C
D
A
B
M└
C
A、AC=AD B、BC=BD
C、AM=OM D、CM=DM
⌒
⌒
⌒
⌒
8
13
注意:解决有关弦的问题时,半径是常用的一种辅助线的添法.往往结合勾股定理计算。
垂径定理的应用:
1、如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离(弦心距)为3厘米,求⊙O的半径。
.O
A
B
E
解:过O作OE⊥AB于E点.
连结OA,在RtAOE中,根据勾股定理:
∴⊙O的半径为5厘米。
练习:
2.在半径为30㎜的⊙O中,弦AB=36㎜,求O到AB的距离。
O
A
B
P
解:过O点作OP⊥AB,连OA.
在Rt⊿AOP中,根据勾股定理:
∴O到AB的距离为24mm。
3.已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。你认为AC和BD有什么关系?为什么?
过O作OE⊥AB,垂足为E,
则AE=BE,CE=DE.
∴ AE-CE=BE-DE
即 AC=BD
.
A
C
D
B
O
E
注意:解决有关弦的问题,过圆心作弦的垂线,也是一种常用辅助线的添法.
解: AC=BD,
理由是:
归纳:
1、解决有关弦的问题时,经常过圆心作弦的垂线、连结半径等辅助线,构成直角三角形。为利用垂径定理和勾股定理创造条件。
.
A
B
O
2、如果弦长为a,弦心距为d,半径为r,弓形的高为h.
⑴d + h = r
⑵
在a、d、r、h四个量中,已知其中任意两个量,可以求出其它两个量.
⑴d + h = r
⑵
1、已知:如图,直径CD⊥AB.
⑴若半径R = 2 ,AB = , 求OE、DE 的长.
⑵若半径R = 2 ,OE = 1 ,求AB、DE 的长.
试一试:
在a、d、r、h四个量中,已知其中任意两个量,可以求出其它两个量.
1、如图,AB为⊙O的直径,CD为弦,CD⊥AB于E.则下列结论中错误的是(??? ? ).
A.∠COE=∠DOE B.CE=DE
C.AE=OE D.BC= BD
c
2、如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM的长的最小值为____最大值为____.
3
5
练习:
3、如图,矩形ABCD与圆O交于点A、B、
E、F,DE=1cm,EF=3cm,则AB=_____cm
5
M
N
4、已知:如图,AB是⊙O直径,与CD相交于点E,已知AE=1cm,BE=5cm,∠DEB=600,求弦CD的长.
.O
C
D
A
B
E
解:连结OA、OB
则OA=OB
∴∠OAB=∠OBA
又∵AC=BD
△AOC≌△BOD(SAS)
5、如图,在圆O中,已知AC=BD,
试说明: OC=OD
∴OC=OD
问题 :你知道赵州桥吗?它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗?
垂径定理的应用:
37.4m
7.2m
A
B
O
C
E
赵州石拱桥
解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
过圆心O作弦AB的垂线OD,与 相交于点C. CD就是拱高.
根据垂径定理得:AD=BD。
由题设
在Rt△OAD中,由勾股定理,得
解得 R≈27.9(m).
答:赵州石拱桥的桥拱半径约为27.9m.
R
D
37.4
7.2
垂径定理的应用
2、如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径.
解:连接OC.
●
O
C
D
E
F
┗
注意闪烁的三角形的特点.
小结:
解决有关弦的问题,经常是
过圆心作弦的垂线,
或作垂直于弦的直径,
连结半径等辅助线,
构成直角三角形,为应用垂径定理创造条件。
.
A
B
O
垂径定理
挑 战自我
1、要把实际问题转变成一个数学问题来解决.
2、熟练地运用垂径定理及其推论、勾股定理,并用方程的思想来解决问题.
3、对于一个圆中的弦长a、圆心到弦的距离d、圆半径r、弓形高h,这四个量中,只要已知其中任意两个量,就可以求出另外两个量,如图有:
⑴d + h = r
⑵
通过这节课的学习,
你有哪些收获?
能与大家一起分享吗?
丰 收 园
结束寄语
读书要从薄到厚,再从厚到薄.
下课了!
同课章节目录
