人教版九年级下册 课件:28.2解直角三角形第2课时(共19张ppt)
文档属性
| 名称 | 人教版九年级下册 课件:28.2解直角三角形第2课时(共19张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 09:45:39 | ||
图片预览



文档简介
(共19张PPT)
28.2 解直角三角形
第2课时
1、了解仰角、俯角的概念,能应用锐角三角函数的知识解决有关实际问题;
2、培养学生分析问题、解决问题的能力.
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
A
B
a
b
c
C
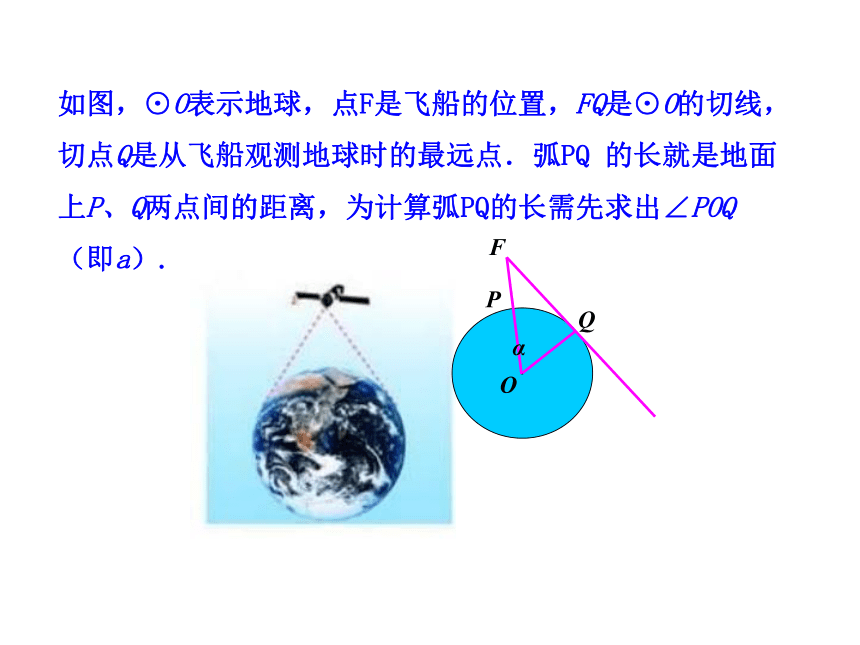
【例1】2003年10月15日“神舟”5号载人航天飞船发射成功.当飞船完成变轨后,就在离地球表面350km的圆形轨道上运行.如图,当飞船运行到地球表面上P点的正上方时,从飞船上最远能直接看到地球上的点在什么位置?这样的最远点与P点的距离是多少?(地球半径约为6 400km,结果精确到0.1km)
【分析】从飞船上能最远直接看到的地球上的点,应是视线与地球相切时的切点.
·
O
Q
F
P
α
如图,⊙O表示地球,点F是飞船的位置,FQ是⊙O的切线,切点Q是从飞船观测地球时的最远点.弧PQ 的长就是地面上P、Q两点间的距离,为计算弧PQ的长需先求出∠POQ
(即a).
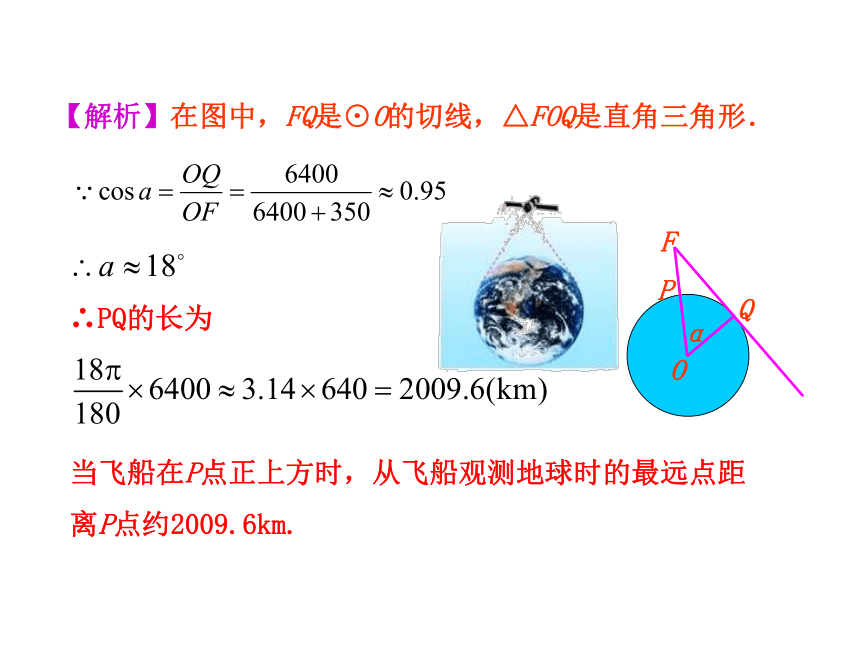
【解析】在图中,FQ是⊙O的切线,△FOQ是直角三角形.
∴PQ的长为
当飞船在P点正上方时,从飞船观测地球时的最远点距离P点约2009.6km.
·
O
Q
F
P
α
铅直线
水平线
视线
视线
仰角
俯角
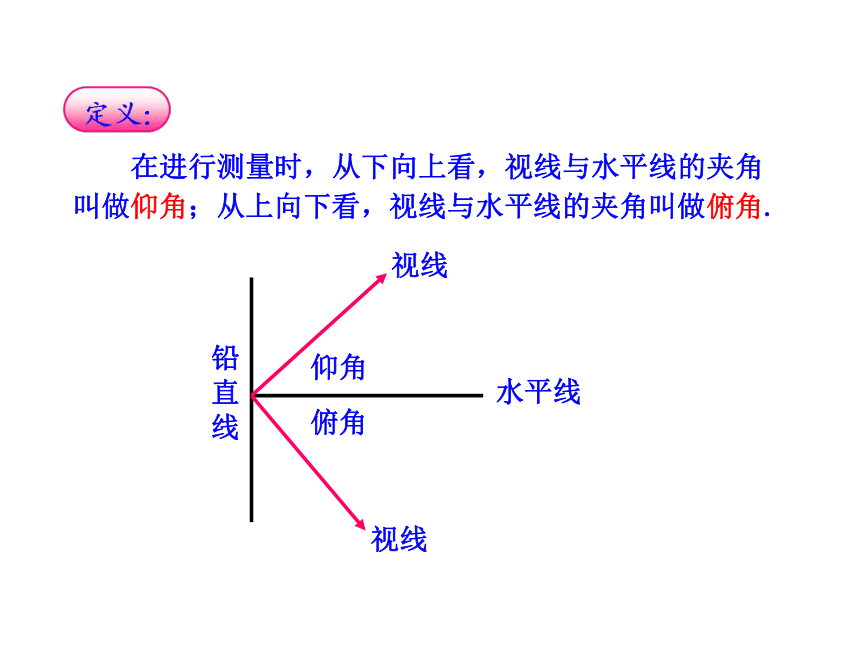
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上向下看,视线与水平线的夹角叫做俯角.
【例2】热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯 角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).
【分析】我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,ɑ =30°,β=60°.
Rt△ABC中,a=30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
A
B
C
D
α
β
仰角
水平线
俯角
【解析】如图,a = 30°,β= 60°,AD=120.
答:这栋楼高约为277.1m.
A
B
C
D
α
β
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处,测得仰角为60°,那么该塔有多高 (小明的身高忽略不计,结果精确到1m).
要解决这问题,我们仍需将其数学化.
30°
60°
D
A
B
C
┌
50m
30°
60°
答:该塔约有43m高.
【解析】如图,根据题意可知,∠A=30°,∠DBC=60°,
AB=50m.设CD=x,则∠ADC=60°,∠BDC=30°,
1.(青海中考)如图,从热气球C上测定建筑物A、B
底部的俯角分别为30°和60°,如果这时气球的高度CD为
150米,且点A、D、B在同一直线上,建筑物A、B间的距离
为( )
A.150 米 B.180 米
C.200 米 D.220 米
C
2.(株洲中考)如图,孔明同学背着一桶水,从山脚出发,沿与地面成角的山坡向上走,送水到山上因今年春季受旱缺水的王奶奶家(B处),AB=80米,则孔明从到上升的高度是 米.
【解析】依题意得,∠ACB=90°.所以sin∠ACB=sin30°=
所以BC=40(米).
【答案】40
3. 建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m)
【解析】在等腰三角形BCD中∠ACD=90°,
BC=DC=40m,
在Rt△ACD中:
所以AB=AC-BC=55.2-40=15.2m
答:棋杆的高度为15.2m.
A
B
C
D
40m
54°
45°
【解析】要使A、C、E在同一直线上,则 ∠ABD是 △BDE 的一个外角,
4. 如图,沿AC方向开山修路.为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD = 140°,BD = 520m,∠D=50°,那么开挖点E离D多远正好能使A,C,E成一直线(精确到0.1m)
50°
140°
520m
A
B
C
E
D
∴∠BED=∠ABD-∠D=90°
答:开挖点E离点D 332.8m正好能使A,C,E成一直线.
5.(鄂州中考)如图,一艘舰艇在海面下500米A点处测得俯角为30°前下方的海底C处有黑匣子信号发出,继续在同一深度直线航行4000米后再次在B点处测得俯角为60°前下方的海底C处有黑匣子信号发出,求海底黑匣子C点距离海面的深度(结果保留根号).
【解析】作CF⊥AB于F,则
∴
∵
∴
∴
∴海底黑匣子C点距离海面的深度
利用解直角三角形的知识解决实际问题的一般过程是:
1.将实际问题抽象为数学问题;
(画出平面图形,转化为解直角三角形的问题)
2.根据条件的特点,适当选用锐角三角函数等去解直角三角形;
3.得到数学问题的答案;
4.得到实际问题的答案.
28.2 解直角三角形
第2课时
1、了解仰角、俯角的概念,能应用锐角三角函数的知识解决有关实际问题;
2、培养学生分析问题、解决问题的能力.
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
A
B
a
b
c
C
【例1】2003年10月15日“神舟”5号载人航天飞船发射成功.当飞船完成变轨后,就在离地球表面350km的圆形轨道上运行.如图,当飞船运行到地球表面上P点的正上方时,从飞船上最远能直接看到地球上的点在什么位置?这样的最远点与P点的距离是多少?(地球半径约为6 400km,结果精确到0.1km)
【分析】从飞船上能最远直接看到的地球上的点,应是视线与地球相切时的切点.
·
O
Q
F
P
α
如图,⊙O表示地球,点F是飞船的位置,FQ是⊙O的切线,切点Q是从飞船观测地球时的最远点.弧PQ 的长就是地面上P、Q两点间的距离,为计算弧PQ的长需先求出∠POQ
(即a).
【解析】在图中,FQ是⊙O的切线,△FOQ是直角三角形.
∴PQ的长为
当飞船在P点正上方时,从飞船观测地球时的最远点距离P点约2009.6km.
·
O
Q
F
P
α
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上向下看,视线与水平线的夹角叫做俯角.
【例2】热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯 角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).
【分析】我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,ɑ =30°,β=60°.
Rt△ABC中,a=30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
A
B
C
D
α
β
仰角
水平线
俯角
【解析】如图,a = 30°,β= 60°,AD=120.
答:这栋楼高约为277.1m.
A
B
C
D
α
β
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处,测得仰角为60°,那么该塔有多高 (小明的身高忽略不计,结果精确到1m).
要解决这问题,我们仍需将其数学化.
30°
60°
D
A
B
C
┌
50m
30°
60°
答:该塔约有43m高.
【解析】如图,根据题意可知,∠A=30°,∠DBC=60°,
AB=50m.设CD=x,则∠ADC=60°,∠BDC=30°,
1.(青海中考)如图,从热气球C上测定建筑物A、B
底部的俯角分别为30°和60°,如果这时气球的高度CD为
150米,且点A、D、B在同一直线上,建筑物A、B间的距离
为( )
A.150 米 B.180 米
C.200 米 D.220 米
C
2.(株洲中考)如图,孔明同学背着一桶水,从山脚出发,沿与地面成角的山坡向上走,送水到山上因今年春季受旱缺水的王奶奶家(B处),AB=80米,则孔明从到上升的高度是 米.
【解析】依题意得,∠ACB=90°.所以sin∠ACB=sin30°=
所以BC=40(米).
【答案】40
3. 建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m)
【解析】在等腰三角形BCD中∠ACD=90°,
BC=DC=40m,
在Rt△ACD中:
所以AB=AC-BC=55.2-40=15.2m
答:棋杆的高度为15.2m.
A
B
C
D
40m
54°
45°
【解析】要使A、C、E在同一直线上,则 ∠ABD是 △BDE 的一个外角,
4. 如图,沿AC方向开山修路.为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD = 140°,BD = 520m,∠D=50°,那么开挖点E离D多远正好能使A,C,E成一直线(精确到0.1m)
50°
140°
520m
A
B
C
E
D
∴∠BED=∠ABD-∠D=90°
答:开挖点E离点D 332.8m正好能使A,C,E成一直线.
5.(鄂州中考)如图,一艘舰艇在海面下500米A点处测得俯角为30°前下方的海底C处有黑匣子信号发出,继续在同一深度直线航行4000米后再次在B点处测得俯角为60°前下方的海底C处有黑匣子信号发出,求海底黑匣子C点距离海面的深度(结果保留根号).
【解析】作CF⊥AB于F,则
∴
∵
∴
∴
∴海底黑匣子C点距离海面的深度
利用解直角三角形的知识解决实际问题的一般过程是:
1.将实际问题抽象为数学问题;
(画出平面图形,转化为解直角三角形的问题)
2.根据条件的特点,适当选用锐角三角函数等去解直角三角形;
3.得到数学问题的答案;
4.得到实际问题的答案.
