人教版七年级上册数学课件:3.2解一元一次方程——合并同类项与移项(共17张ppt)
文档属性
| 名称 | 人教版七年级上册数学课件:3.2解一元一次方程——合并同类项与移项(共17张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 09:44:14 | ||
图片预览






文档简介
1.等式的性质
① 等式的两边同时加或减同一个数或式,结果仍相等.
② 等式的两边同时乘同一个数,或除以同一个不为0的数,结果仍相等.
复习
2. 合并同类项解一元一次方程的一般步骤
(1)合并同类项;
(2)化系数为1。
注意:方程的解的一般形式为:
(1)这两个方程中,含未知数的项和常数项分布有何特点?
(2)解这些方程用到了哪几个步骤?依据分别是什么?
解:合并同类项,得
- x=- 15
化系数为1,得
x=15
解:合并同类项,得
化系数为1,得
x=72
(1)2x-3x= - 7- 8
回顾:利用合并同类项解下列一元一次方程:
把一些图书分给某班同学阅读,如果每人3本,则剩余20本;若每人4本,则还缺少25本,这个班的学生有多少人?
分析:
设这个班有x名学生
这批书共有(3x+20)本
这批书共有(4x-25)本
表示同一个量的两个不同的式子相等(即:这批书的总数是一个定值)
3x+20=4x-25
思考:我们还可以用合并同类项法去解这个方程吗?
如何才能使这个方程向“x=a”的形式转化?
分析:解方程,就是把方程变形,变为 x = a(a为常数)的形式.
上面方程的变形,相当于把原方程左边的20变为-20移到右边,把右边的4x变为-4x移到左边.
利用等式的性质解方程
3x-4x=-25-20
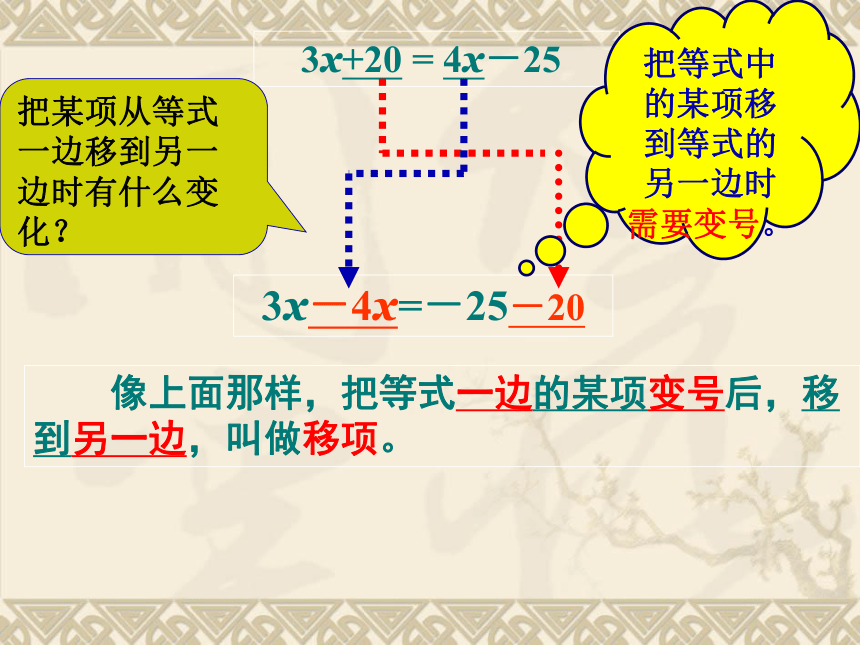
3x+20 = 4x-25
把某项从等式一边移到另一边时有什么变化?
把等式中的某项移到等式的另一边时需要变号。
像上面那样,把等式一边的某项变号后,移到另一边,叫做移项。
例如:下列移项正确的是( )
A. 3x+b=0,则3x=b; B. 2x=x-1,则2x-x=1 ;
C.4x-2=5+2x,则4x-2x=5-2 ;
D. 2+x-3=2x+1,则2-3-1=2x-x。
D
注意:关于移项
1. 所移的项一 定要变号;
2. 不能与加法交换律混淆;
3.依据是:等式的性质1;
4.目的是:为了得到形如ax=b的方程。
⑴ 方程3x-4=1,移项得:3x=1 .
⑵ 方程2x+3=5,移项得:2x= .
⑶ 方程5x=x+1,移项得: .
⑷ 方程2x-7=-5x,移项得: .
⑸ 方程4x=3x-8,移项得: .
⑹ 方程x=3x-5x-9,移项得: .
+4
5-3
5x-x=1
2x+5x=7
4x-3x=-8
X-3x+5x=-9
注意:移项要改变符号;移项时含有未知数的项放在等号左边,常数项放在等号右边,即“x=a”的形式。
学以致用:将下列各式移项(口答)
解:移项得:
合并同类项:
系数化为1得:
解这类方程的一般步骤
(依据是:等式的性质1)
(依据是:乘法分配率的逆用)
(依据是:等式的性质2)
解这个方程的具体过程是:
解形如“ax+b=cx+d”的方程的
一般步骤:
(1)移项;
(2)合并同类项;
(3)化未知数的系数为1。
例3 解下列方程
解:
移项,得
合并同类项,得
系数化为1,得
解:
移项,得
合并同类项,得
系数化为1,得
解下列方程:(用移项,合并同类项法)
4
已知x=1是关于x的方程3m+8x=m+x的解,求m的值。
3m-m = 1- 8
2m =-7
m = -3.5
解 : 把 x = 1 代入方程, 得:
3m + 8 = m+1
约公元825年,中亚细亚数学家阿尔—花拉子米写了一本代数书,重点论述怎样解方程。这本书的拉丁译本为《对消与还原》。“对消”与“还原”是什么意思呢?
其实所谓的“对消”简单的说就是指“合并同类项”,“还原”是指“移项”。
(1)一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项。
(2)移项的依据是等式的性质1.
1.移项
2.解形如“ax+b=cx+d”的方程的一般步骤和依据:
(1)移项;(2)合并同类项;(3)化未知数的系数为1。
作业:
1.课本P91:第3题(作业本)
2.练习册( P69 ):3.2 合并同类项与移项(一)
① 等式的两边同时加或减同一个数或式,结果仍相等.
② 等式的两边同时乘同一个数,或除以同一个不为0的数,结果仍相等.
复习
2. 合并同类项解一元一次方程的一般步骤
(1)合并同类项;
(2)化系数为1。
注意:方程的解的一般形式为:
(1)这两个方程中,含未知数的项和常数项分布有何特点?
(2)解这些方程用到了哪几个步骤?依据分别是什么?
解:合并同类项,得
- x=- 15
化系数为1,得
x=15
解:合并同类项,得
化系数为1,得
x=72
(1)2x-3x= - 7- 8
回顾:利用合并同类项解下列一元一次方程:
把一些图书分给某班同学阅读,如果每人3本,则剩余20本;若每人4本,则还缺少25本,这个班的学生有多少人?
分析:
设这个班有x名学生
这批书共有(3x+20)本
这批书共有(4x-25)本
表示同一个量的两个不同的式子相等(即:这批书的总数是一个定值)
3x+20=4x-25
思考:我们还可以用合并同类项法去解这个方程吗?
如何才能使这个方程向“x=a”的形式转化?
分析:解方程,就是把方程变形,变为 x = a(a为常数)的形式.
上面方程的变形,相当于把原方程左边的20变为-20移到右边,把右边的4x变为-4x移到左边.
利用等式的性质解方程
3x-4x=-25-20
3x+20 = 4x-25
把某项从等式一边移到另一边时有什么变化?
把等式中的某项移到等式的另一边时需要变号。
像上面那样,把等式一边的某项变号后,移到另一边,叫做移项。
例如:下列移项正确的是( )
A. 3x+b=0,则3x=b; B. 2x=x-1,则2x-x=1 ;
C.4x-2=5+2x,则4x-2x=5-2 ;
D. 2+x-3=2x+1,则2-3-1=2x-x。
D
注意:关于移项
1. 所移的项一 定要变号;
2. 不能与加法交换律混淆;
3.依据是:等式的性质1;
4.目的是:为了得到形如ax=b的方程。
⑴ 方程3x-4=1,移项得:3x=1 .
⑵ 方程2x+3=5,移项得:2x= .
⑶ 方程5x=x+1,移项得: .
⑷ 方程2x-7=-5x,移项得: .
⑸ 方程4x=3x-8,移项得: .
⑹ 方程x=3x-5x-9,移项得: .
+4
5-3
5x-x=1
2x+5x=7
4x-3x=-8
X-3x+5x=-9
注意:移项要改变符号;移项时含有未知数的项放在等号左边,常数项放在等号右边,即“x=a”的形式。
学以致用:将下列各式移项(口答)
解:移项得:
合并同类项:
系数化为1得:
解这类方程的一般步骤
(依据是:等式的性质1)
(依据是:乘法分配率的逆用)
(依据是:等式的性质2)
解这个方程的具体过程是:
解形如“ax+b=cx+d”的方程的
一般步骤:
(1)移项;
(2)合并同类项;
(3)化未知数的系数为1。
例3 解下列方程
解:
移项,得
合并同类项,得
系数化为1,得
解:
移项,得
合并同类项,得
系数化为1,得
解下列方程:(用移项,合并同类项法)
4
已知x=1是关于x的方程3m+8x=m+x的解,求m的值。
3m-m = 1- 8
2m =-7
m = -3.5
解 : 把 x = 1 代入方程, 得:
3m + 8 = m+1
约公元825年,中亚细亚数学家阿尔—花拉子米写了一本代数书,重点论述怎样解方程。这本书的拉丁译本为《对消与还原》。“对消”与“还原”是什么意思呢?
其实所谓的“对消”简单的说就是指“合并同类项”,“还原”是指“移项”。
(1)一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项。
(2)移项的依据是等式的性质1.
1.移项
2.解形如“ax+b=cx+d”的方程的一般步骤和依据:
(1)移项;(2)合并同类项;(3)化未知数的系数为1。
作业:
1.课本P91:第3题(作业本)
2.练习册( P69 ):3.2 合并同类项与移项(一)
