人教版数学九年级上册 第24章 圆 24.1.3 弧、弦、圆心角 课件(共32张PPT)
文档属性
| 名称 | 人教版数学九年级上册 第24章 圆 24.1.3 弧、弦、圆心角 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 09:29:17 | ||
图片预览


文档简介
24.1.3 弧、弦、圆心角
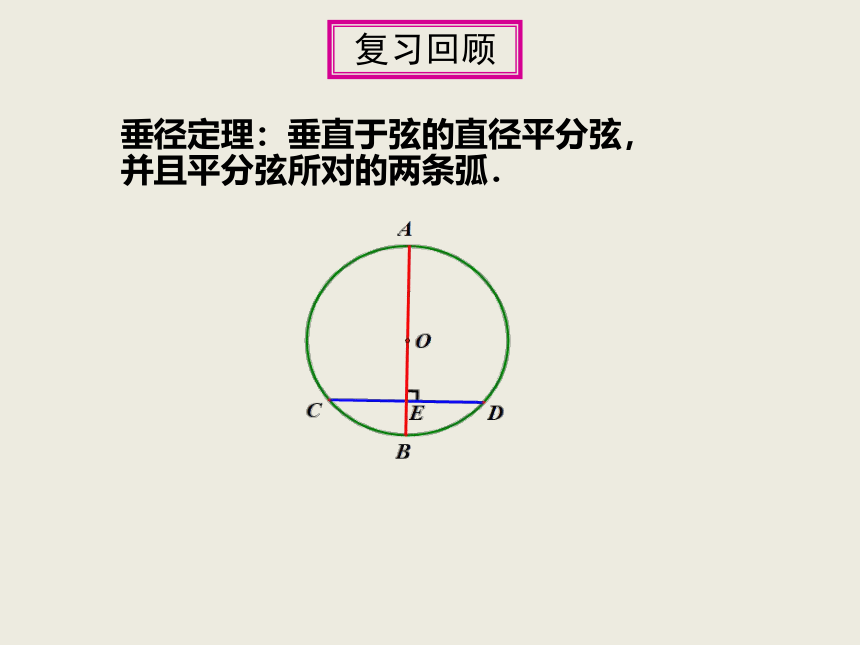
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
复习回顾
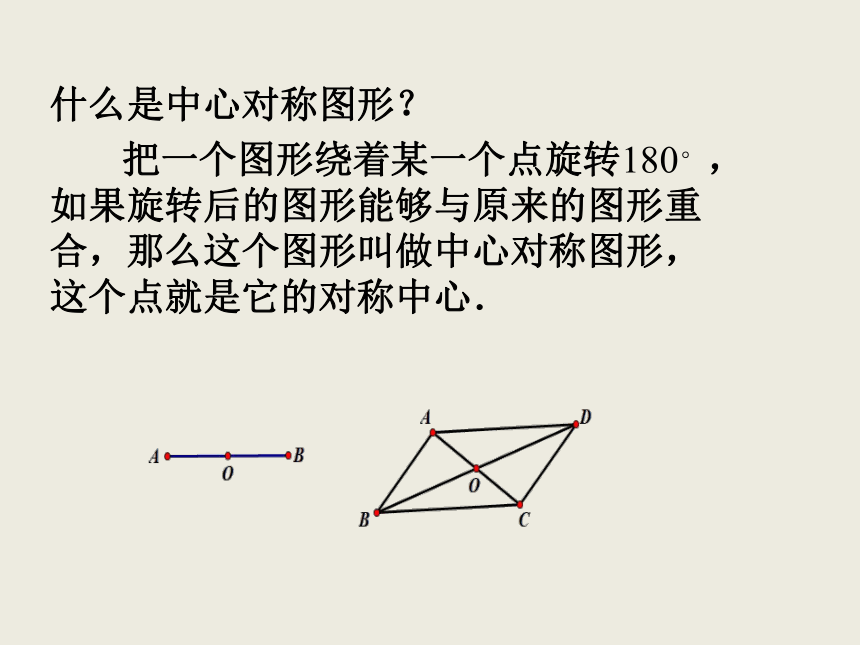
什么是中心对称图形?
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
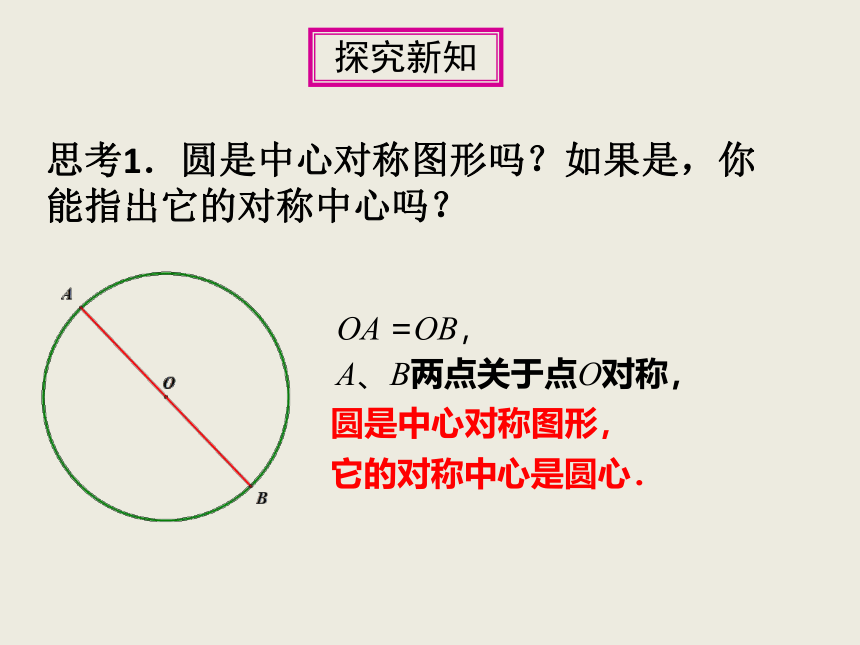
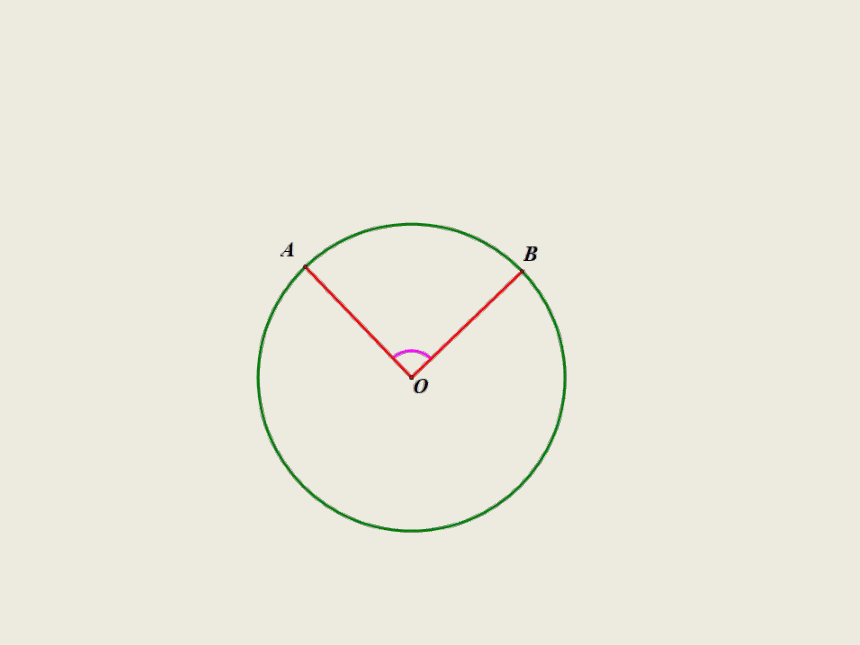
思考1.圆是中心对称图形吗?如果是,你能指出它的对称中心吗?
圆是中心对称图形,
它的对称中心是圆心.
探究新知
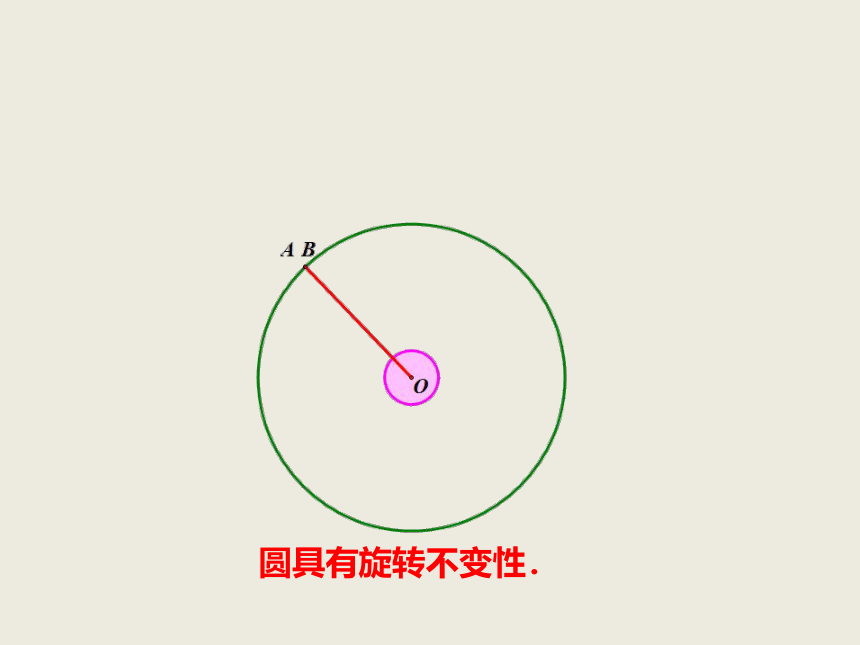
OA =OB,
A、B两点关于点O对称,
思考2.把 O绕圆心O旋转任意一个角度后,还能和原来的图形重合吗?
圆具有旋转不变性.
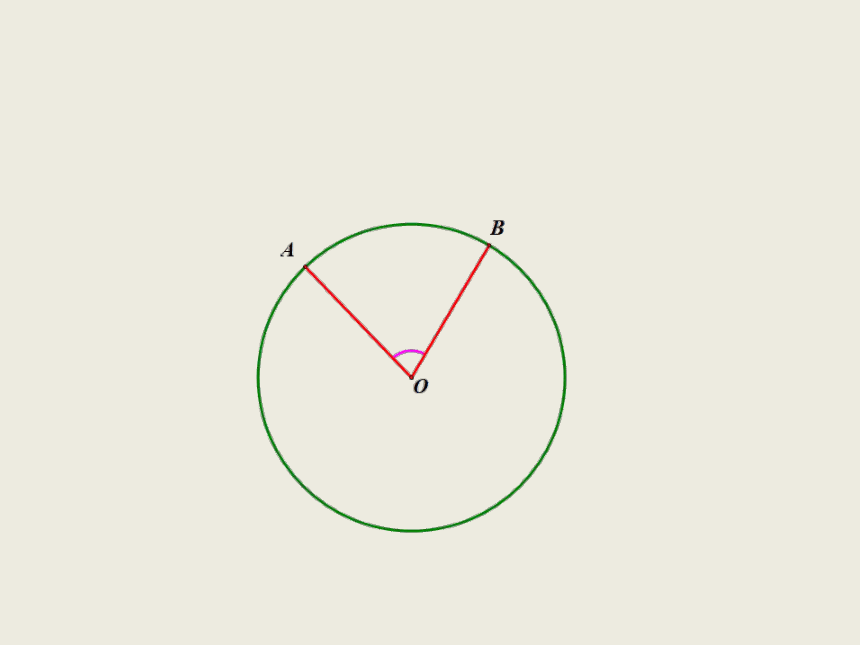
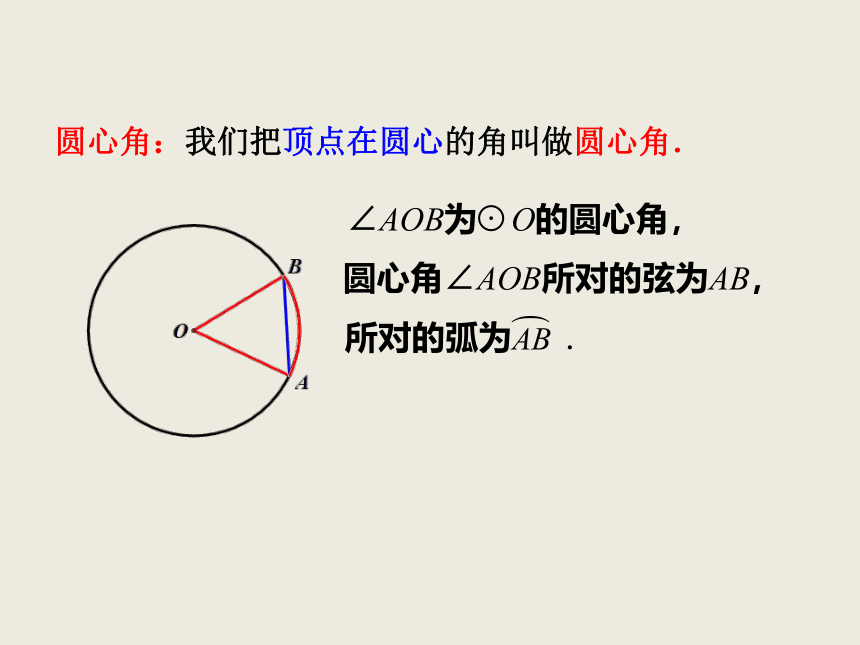
圆心角:我们把顶点在圆心的角叫做圆心角.
所对的弧为 .
圆心角∠AOB所对的弦为AB,
∠AOB为 O的圆心角,
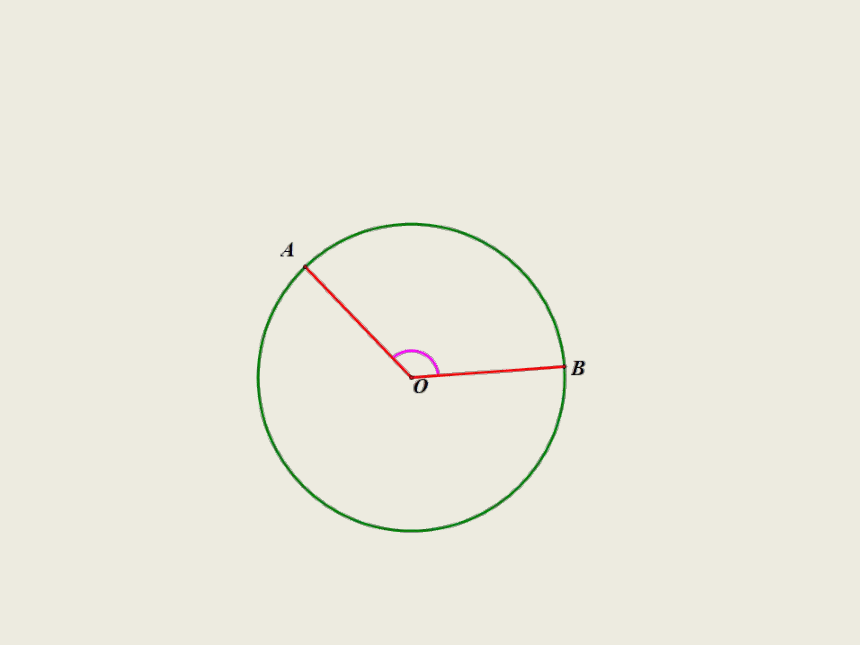
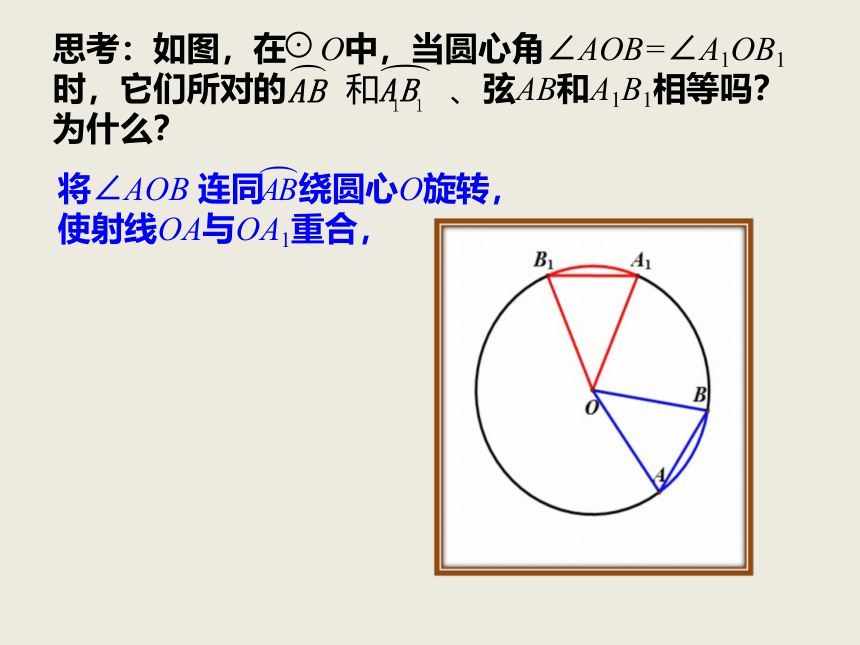
思考:如图,在 O中,当圆心角∠AOB=∠A1OB1时,它们所对的 和 、弦AB和A1B1相等吗?为什么?
将∠AOB 连同 绕圆心O旋转,
使射线OA与OA1重合,
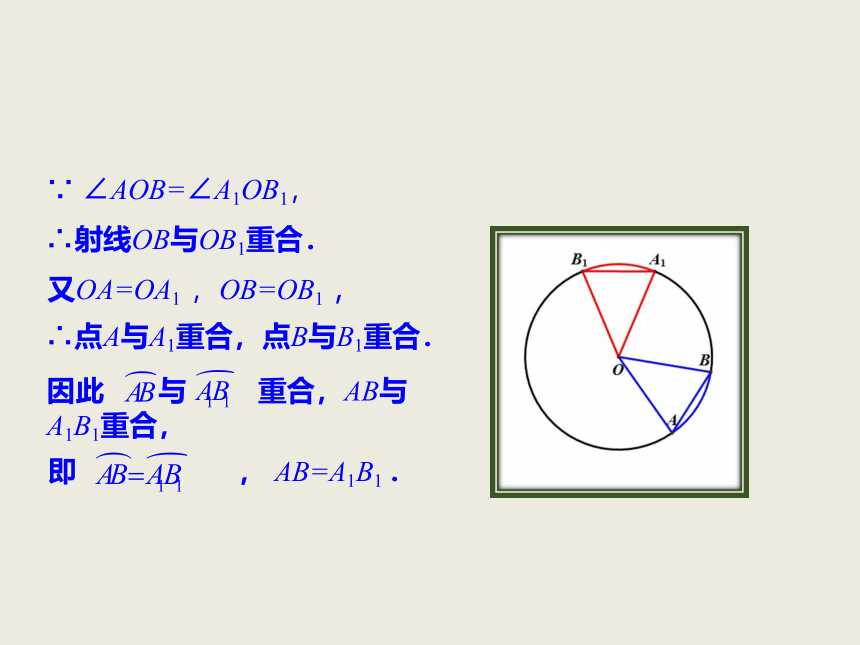
∵ ∠AOB=∠A1OB1,
∴射线OB与OB1重合.
又OA=OA1 ,OB=OB1 ,
即 , AB=A1B1 .
∴点A与A1重合,点B与B1重合.
因此 与 重合,AB与A1B1重合,
做一做:在纸上画两个等圆,点A,B在⊙O上,A1,B1在⊙O1上,使∠AOB=∠A1O1B1 ,连接AB和A1B1 ,则 与 ,弦AB与A1B1还相等吗?
定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
α
α
∠AOB=∠A1OB1,
∴ = ,AB=A1B1 .
∵ OA,OB,OA1,OB1是 O的半径,
思考:如图,两同心圆中, ,问:
(1) 与 是否相等?
(2) 与 是否相等?
不相等
不相等
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧也分别相等.
圆心角等
弦 等
弧 等
知一推二
如图,AB,CD是 O的两条弦.
(1)如果AB=CD,那么________,______________.
∠AOB=∠COD
(2)如果 ,那么________,______________.
(3)如果∠AOB=∠COD,那么_______,_________.
AB=CD
∠AOB=∠COD
AB=CD
概念巩固
例1 如图,在 O中, ,∠ACB=60°.
求证: ∠AOB=∠BOC=∠AOC.
例题讲解
A
B
C
O
∴AB=AC,△ABC是等腰三角形.
又 ∠ACB=60°,
∴△ABC是等边三角形,AB=BC=CA.
∴∠AOB=∠BOC=∠AOC.
证明: ? ,
A
B
C
O
证法一: ∵AD=BC,
∴AB=CD.
.
,
.
例2 已知:如图所示,在 O中, AD=BC .
求证:AB=CD.
例2 已知:如图所示,在 O中, AD=BC .
求证:AB=CD.
证法二:连接OA,OD,OB,OC.
∴AB=CD.
∵AD=BC,
∴∠AOD=∠BOC.
∴∠AOD+∠BOD=∠BOC+ ∠BOD,
∴∠AOB=∠DOC.
例3 如图,AB、CD是 O的两条直径,BE=BD,
求证: .
证法一:连接AC.
∴∠AOC=∠BOD.
∴AC=BD,
又BE=BD,
∴AC=BE.
∴
.
∵AB,CD是 O的两条直径,
证法二:连接AC、OE,
∴∠AOC=∠BOD,
∵BE=BD,
∵AB、CD是⊙O的两条直径,
∴∠BOE=∠BOD,
∴∠AOC=∠BOE,
∴
例3 如图,AB、CD是 O的两条直径,BE=BD,
求证: .
探究 如图,AB,CD是 O的两条弦,OE⊥AB
于E,OF⊥CD于F.
(1)如果AB=CD, OE与OF相等吗?为什么?
(2)如果OE=OF, AB与CD相等吗?为什么?
∵ OE⊥AB , OF⊥CD ,
∴Rt△AOE≌ Rt △COF.
∴OE=OF.
证明:
∵AB=CD ,
AE= AB , CF= CD .
∴AE=CF.
∵OA=OC ,
OE与OF相等.
∴∠AEO=∠CFO=90°,
Rt △AOE≌ Rt △COF
OE=OF,OA=OC,∠AEO=∠CFO=90°
AB=CD
分析:
探究 如图,AB,CD是 O的两条弦,OE⊥AB
于E,OF⊥CD于F.
(2)如果OE=OF, AB与CD相等吗?为什么?
课堂小结
圆是中心对称图形,圆具有旋转不变性;
定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
圆心角等
弦 等
弧 等
证明弧等的方法:
等弧的定义;
垂径定理;
弧、弦、圆心角之间的关系。
课后作业
1.如图, O中, ,∠C=75°.
求∠A的度数.
2.如图,A,B是 O上两点,
∠AOB=120°,C是 的中点.
求证:四边形OACB是菱形.
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
复习回顾
什么是中心对称图形?
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
思考1.圆是中心对称图形吗?如果是,你能指出它的对称中心吗?
圆是中心对称图形,
它的对称中心是圆心.
探究新知
OA =OB,
A、B两点关于点O对称,
思考2.把 O绕圆心O旋转任意一个角度后,还能和原来的图形重合吗?
圆具有旋转不变性.
圆心角:我们把顶点在圆心的角叫做圆心角.
所对的弧为 .
圆心角∠AOB所对的弦为AB,
∠AOB为 O的圆心角,
思考:如图,在 O中,当圆心角∠AOB=∠A1OB1时,它们所对的 和 、弦AB和A1B1相等吗?为什么?
将∠AOB 连同 绕圆心O旋转,
使射线OA与OA1重合,
∵ ∠AOB=∠A1OB1,
∴射线OB与OB1重合.
又OA=OA1 ,OB=OB1 ,
即 , AB=A1B1 .
∴点A与A1重合,点B与B1重合.
因此 与 重合,AB与A1B1重合,
做一做:在纸上画两个等圆,点A,B在⊙O上,A1,B1在⊙O1上,使∠AOB=∠A1O1B1 ,连接AB和A1B1 ,则 与 ,弦AB与A1B1还相等吗?
定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
α
α
∠AOB=∠A1OB1,
∴ = ,AB=A1B1 .
∵ OA,OB,OA1,OB1是 O的半径,
思考:如图,两同心圆中, ,问:
(1) 与 是否相等?
(2) 与 是否相等?
不相等
不相等
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧也分别相等.
圆心角等
弦 等
弧 等
知一推二
如图,AB,CD是 O的两条弦.
(1)如果AB=CD,那么________,______________.
∠AOB=∠COD
(2)如果 ,那么________,______________.
(3)如果∠AOB=∠COD,那么_______,_________.
AB=CD
∠AOB=∠COD
AB=CD
概念巩固
例1 如图,在 O中, ,∠ACB=60°.
求证: ∠AOB=∠BOC=∠AOC.
例题讲解
A
B
C
O
∴AB=AC,△ABC是等腰三角形.
又 ∠ACB=60°,
∴△ABC是等边三角形,AB=BC=CA.
∴∠AOB=∠BOC=∠AOC.
证明: ? ,
A
B
C
O
证法一: ∵AD=BC,
∴AB=CD.
.
,
.
例2 已知:如图所示,在 O中, AD=BC .
求证:AB=CD.
例2 已知:如图所示,在 O中, AD=BC .
求证:AB=CD.
证法二:连接OA,OD,OB,OC.
∴AB=CD.
∵AD=BC,
∴∠AOD=∠BOC.
∴∠AOD+∠BOD=∠BOC+ ∠BOD,
∴∠AOB=∠DOC.
例3 如图,AB、CD是 O的两条直径,BE=BD,
求证: .
证法一:连接AC.
∴∠AOC=∠BOD.
∴AC=BD,
又BE=BD,
∴AC=BE.
∴
.
∵AB,CD是 O的两条直径,
证法二:连接AC、OE,
∴∠AOC=∠BOD,
∵BE=BD,
∵AB、CD是⊙O的两条直径,
∴∠BOE=∠BOD,
∴∠AOC=∠BOE,
∴
例3 如图,AB、CD是 O的两条直径,BE=BD,
求证: .
探究 如图,AB,CD是 O的两条弦,OE⊥AB
于E,OF⊥CD于F.
(1)如果AB=CD, OE与OF相等吗?为什么?
(2)如果OE=OF, AB与CD相等吗?为什么?
∵ OE⊥AB , OF⊥CD ,
∴Rt△AOE≌ Rt △COF.
∴OE=OF.
证明:
∵AB=CD ,
AE= AB , CF= CD .
∴AE=CF.
∵OA=OC ,
OE与OF相等.
∴∠AEO=∠CFO=90°,
Rt △AOE≌ Rt △COF
OE=OF,OA=OC,∠AEO=∠CFO=90°
AB=CD
分析:
探究 如图,AB,CD是 O的两条弦,OE⊥AB
于E,OF⊥CD于F.
(2)如果OE=OF, AB与CD相等吗?为什么?
课堂小结
圆是中心对称图形,圆具有旋转不变性;
定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
圆心角等
弦 等
弧 等
证明弧等的方法:
等弧的定义;
垂径定理;
弧、弦、圆心角之间的关系。
课后作业
1.如图, O中, ,∠C=75°.
求∠A的度数.
2.如图,A,B是 O上两点,
∠AOB=120°,C是 的中点.
求证:四边形OACB是菱形.
同课章节目录
