人教版数学九年级下册-26.1.2反比例函数的图象和性质反比例函数k的几何意义课件(共17张ppt)
文档属性
| 名称 | 人教版数学九年级下册-26.1.2反比例函数的图象和性质反比例函数k的几何意义课件(共17张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 09:41:17 | ||
图片预览




文档简介
课题:反比例函数k的几何意义
科目:数学
年级:初三年级
主讲人:
反比例函数K的几何意义
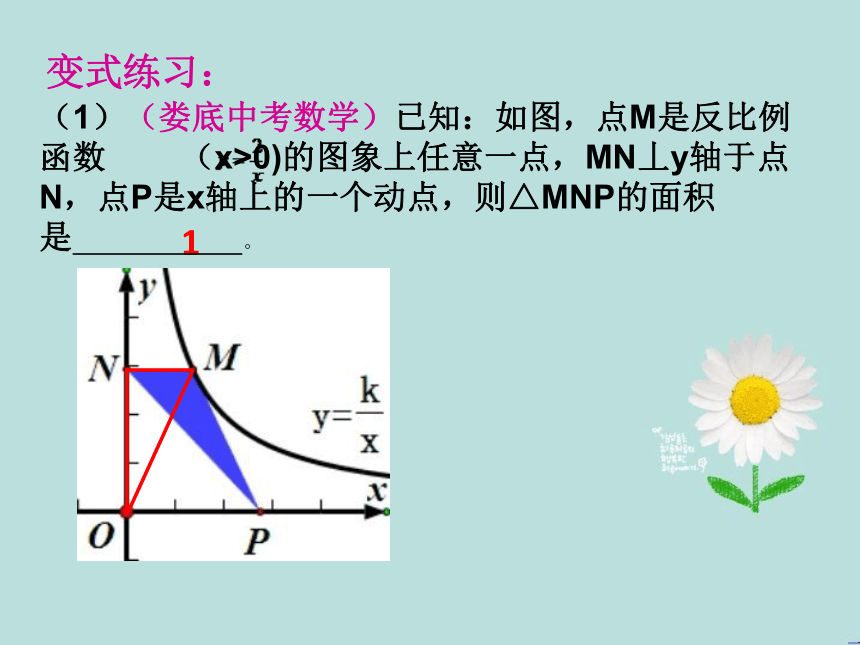
(一)基本图形1及其应用:
(x,y)
解:∵双曲线 (k≠0)在第一象限,∴k>0,
延长线段BA,交y轴于点E,
∵AB∥x轴,
∴AE⊥y轴,
∴四边形AEOD是矩形,
∵点A在双曲线上,
∴S矩形AEOD=4,
同理S矩形OCBE=k,
∵S矩形ABCD=S矩形OCBE-S矩形AEOD=k-4=8,
∴k=12.
例1:如图,点A在双曲线 上,点B在双曲线 (k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,
若矩形ABCD的面积是8,则k的值为 ____。
E
12
1
变式练习:
(1)
(1)(娄底中考数学)已知:如图,点M是反比例函数 (x>0)的图象上任意一点,MN丄y轴于点N,点P是x轴上的一个动点,则△MNP的面积是 。
(2)( 永州中考)
C
C
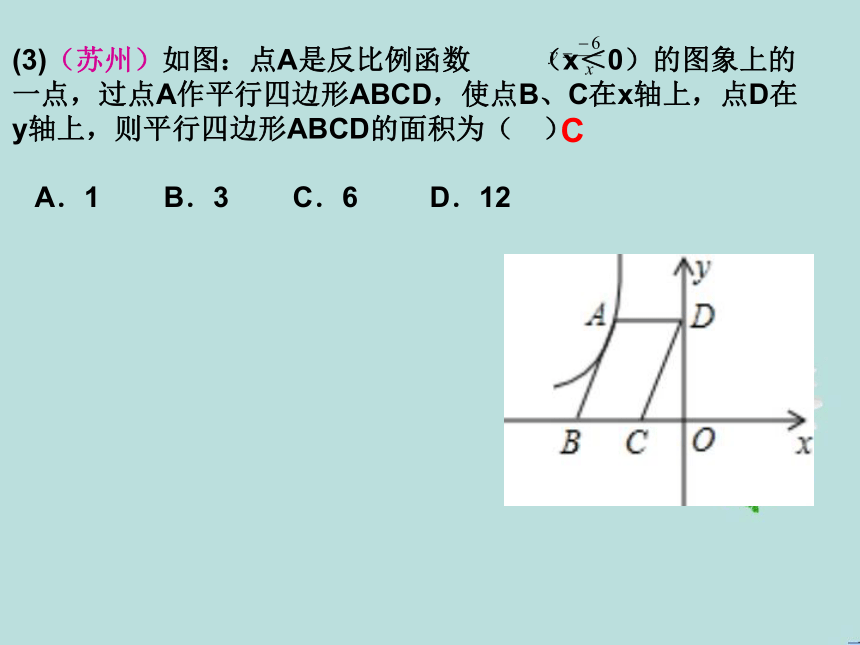
(3)(苏州)如图:点A是反比例函数 (x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上,则平行四边形ABCD的面积为( )
A.1 B.3 C.6 D.12
图中面积相等的图形有哪些?
(二)基本图形2及其应用:
例2:如图,点A、B、是双曲线 上的点,分别经过A、B两点向x轴、y轴作垂线段,若S阴影=1,则S1+S2 =
4
变式练习:
(1)如图,点A(x1,y1)、B(x2,y2)都在双曲线(x>0)上,且x2-x1=4,y1-y2=2.分别过点A、B向x轴、y轴作垂线,垂足分别为C、D、E、F,AC与BF相交于点G,四边形FOCG的面积为2,五边形AEODB的面积为14,求双曲线的解析式。
=8
(2)(遵义中考改)如图,在坐标平面上有两点A(2,3)和B(6,1),求△AOB的面积;
图中面积相等的图形有哪些?
(三)基本图形3及其应用
例4:(河南中考)如图,矩形OABC的两边在坐标轴上,且与反比例函数 的图像交于点E、F,其中点F是AB的中点,若四边形OEBF的面积为2,则k=______。
2
变式一:
若将经过矩形OABC边AB的中点E,改为“经过矩形
OABC边BC的中点F”,其它不变, k值是否改变?
E
F
M
D
F
M
O
B
A
变式二(?内江)矩形OABC的两边在坐标轴上,且与反比例函数 (x>0)的图像交于点E、F,反比例函数图像经过矩形OABC的对角线的交点D,若四边形OEBF的面积为2,则k=______。
小结
★数学思想方法:
数形结合、转化思想、整体应用
★解题方法:运用K的几何意义、割补法解面积问题
学会找到复杂图形中的基本图形
教师寄语:
做人必有底线,如双曲线与坐标轴之间,永远不能触底越界。
做事必有坚持,如K的几何意义一般,不因外界的变化而改变。
科目:数学
年级:初三年级
主讲人:
反比例函数K的几何意义
(一)基本图形1及其应用:
(x,y)
解:∵双曲线 (k≠0)在第一象限,∴k>0,
延长线段BA,交y轴于点E,
∵AB∥x轴,
∴AE⊥y轴,
∴四边形AEOD是矩形,
∵点A在双曲线上,
∴S矩形AEOD=4,
同理S矩形OCBE=k,
∵S矩形ABCD=S矩形OCBE-S矩形AEOD=k-4=8,
∴k=12.
例1:如图,点A在双曲线 上,点B在双曲线 (k≠0)上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为D、C,
若矩形ABCD的面积是8,则k的值为 ____。
E
12
1
变式练习:
(1)
(1)(娄底中考数学)已知:如图,点M是反比例函数 (x>0)的图象上任意一点,MN丄y轴于点N,点P是x轴上的一个动点,则△MNP的面积是 。
(2)( 永州中考)
C
C
(3)(苏州)如图:点A是反比例函数 (x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上,则平行四边形ABCD的面积为( )
A.1 B.3 C.6 D.12
图中面积相等的图形有哪些?
(二)基本图形2及其应用:
例2:如图,点A、B、是双曲线 上的点,分别经过A、B两点向x轴、y轴作垂线段,若S阴影=1,则S1+S2 =
4
变式练习:
(1)如图,点A(x1,y1)、B(x2,y2)都在双曲线(x>0)上,且x2-x1=4,y1-y2=2.分别过点A、B向x轴、y轴作垂线,垂足分别为C、D、E、F,AC与BF相交于点G,四边形FOCG的面积为2,五边形AEODB的面积为14,求双曲线的解析式。
=8
(2)(遵义中考改)如图,在坐标平面上有两点A(2,3)和B(6,1),求△AOB的面积;
图中面积相等的图形有哪些?
(三)基本图形3及其应用
例4:(河南中考)如图,矩形OABC的两边在坐标轴上,且与反比例函数 的图像交于点E、F,其中点F是AB的中点,若四边形OEBF的面积为2,则k=______。
2
变式一:
若将经过矩形OABC边AB的中点E,改为“经过矩形
OABC边BC的中点F”,其它不变, k值是否改变?
E
F
M
D
F
M
O
B
A
变式二(?内江)矩形OABC的两边在坐标轴上,且与反比例函数 (x>0)的图像交于点E、F,反比例函数图像经过矩形OABC的对角线的交点D,若四边形OEBF的面积为2,则k=______。
小结
★数学思想方法:
数形结合、转化思想、整体应用
★解题方法:运用K的几何意义、割补法解面积问题
学会找到复杂图形中的基本图形
教师寄语:
做人必有底线,如双曲线与坐标轴之间,永远不能触底越界。
做事必有坚持,如K的几何意义一般,不因外界的变化而改变。
