人教版数学九年级下册26.2探究反比例函数的图象和性质课件(共31张ppt)
文档属性
| 名称 | 人教版数学九年级下册26.2探究反比例函数的图象和性质课件(共31张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 09:39:47 | ||
图片预览






文档简介
反比例函数的图象与性质
数缺形时少直觉,形少数时难入微.
已知一次函数y=kx+b(k≠0)的图象是
反比例函数 (k≠0)的图象是什么呢?
让我们一起画个反比例函数的图象看看,好吗?
“预见性”,猜一猜
反比例函数的图象又会是什么样子呢?
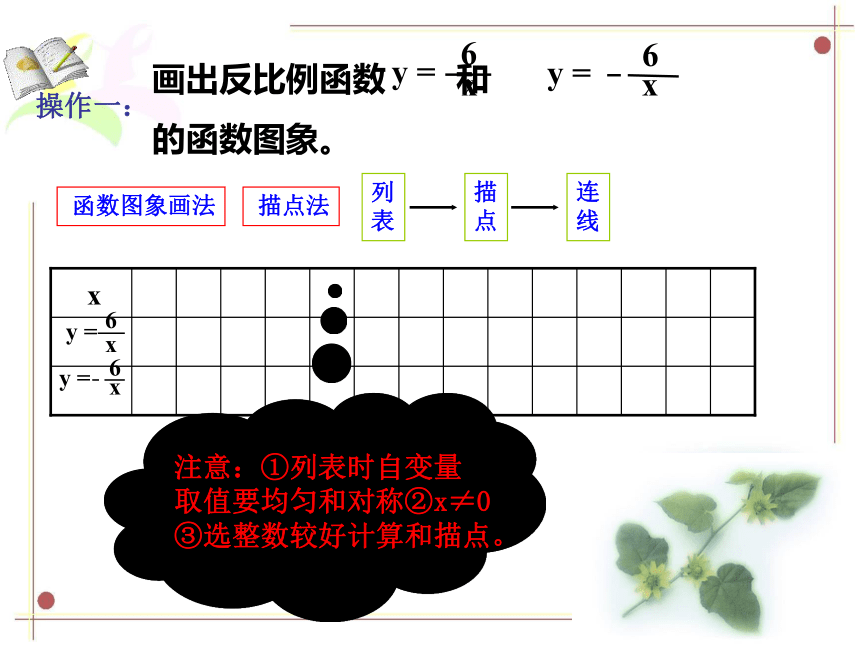
你还记得作函数图象的一般步骤吗?
给反比例函数“照相”
用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线(按自变量从小到大的顺序,用一条平滑的曲线连接起来).
x
画出反比例函数 和
的函数图象。
y =
x
6
y =
x
6
函数图象画法
列
表
描
点
连
线
y =
x
6
y =
x
6
描点法
注意:①列表时自变量
取值要均匀和对称②x≠0
③选整数较好计算和描点。
操作一:
1
2
3
4
5
6
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y =
x
6
y =-
x
6
-6
x
y
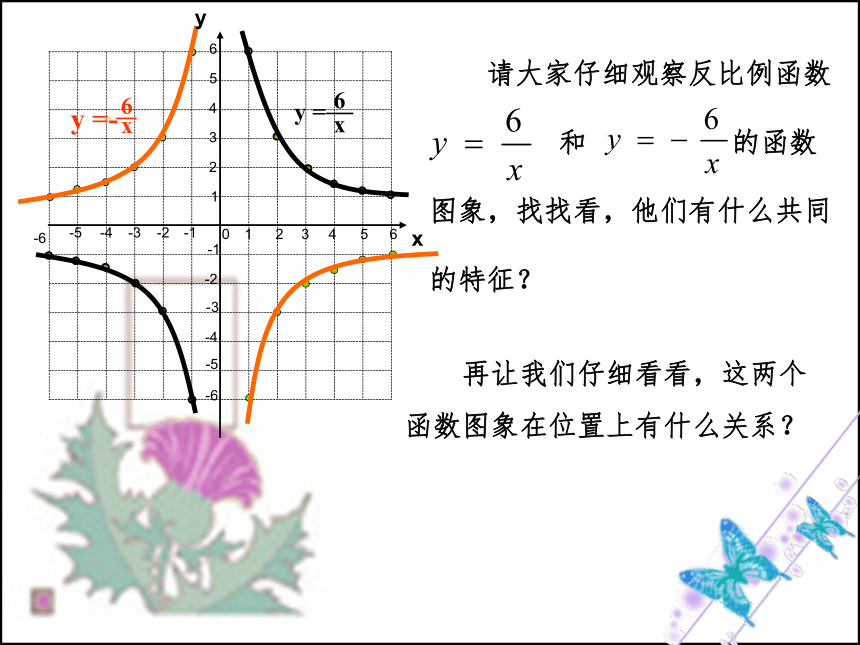
请大家仔细观察反比例函数
和 的函数
图象,找找看,他们有什么共同
的特征?
再让我们仔细看看,这两个
函数图象在位置上有什么关系?
操作二:
比一比:
同桌两人分别画出函数 或
的图象,看谁画得又快又好.
找一找:
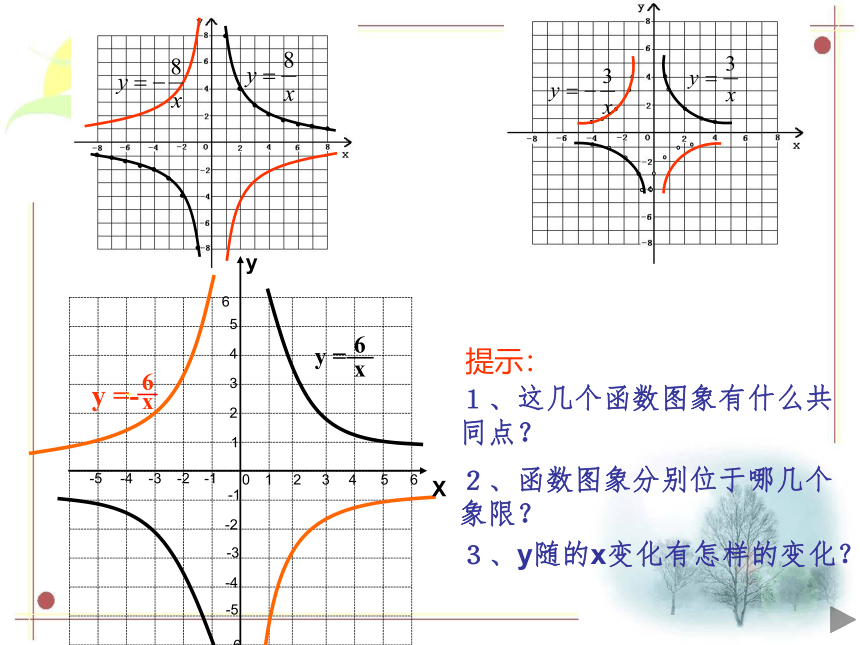
1、这几个函数图象有什么共同点?
2、函数图象分别位于哪几个象限?
3、y随x的变化有怎样的变化?
根据大家所画出的函数图象,从以下几个方面出发,你
能发现反比例函数 的图象及性质有哪些?
1
2
3
4
5
6
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y =
x
6
y =-
x
6
X
y
1、这几个函数图象有什么共同点?
2、函数图象分别位于哪几个象限?
3、y随的x变化有怎样的变化?
提示:
由两支曲线组成的.因此称它的图象为双曲线;
当k>0时,两支双曲线分别位于第一,三象限内;
当k<0时,两支双曲线分别位于第二,四象限内;
当k>0时,在每一象限内,y随x的增大而减小;
当k<0时,在每一象限内,y随x的增大而增大.
反比例函数的图象无限接近于x,y轴,但永远不能到达x,y轴
⑴反比例函数的图象是轴对称图形.直线y=x和y=-x都是它的对称轴;
⑵反比例函数 与 的图象关于x轴对称,也关于y轴对称。
反比例函数的图象和性质
形状
位置
增减性
图象的发展趋势
对称性
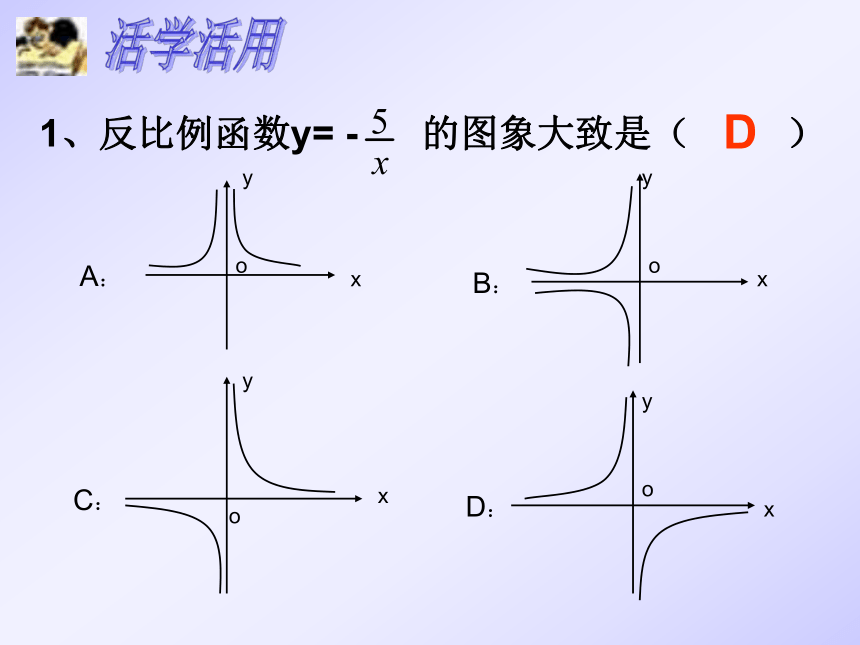
A:
x
y
o
B:
x
y
o
D:
x
y
o
C:
x
y
o
1、反比例函数y= - 的图象大致是( )
D
函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
函数 ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三
二、四
一
减小
增大
减小
2.若关于x,y的函数 图象位于第一、三象限,
则k的取值范围是_______________
k>-1
3.甲乙两地相距100km,一辆汽车从甲地开往乙地,
把汽车到达乙地所用的时间y(h)表示为汽车的平均
速度x(km/h)的函数,则这个函数的图象大致是( )
C
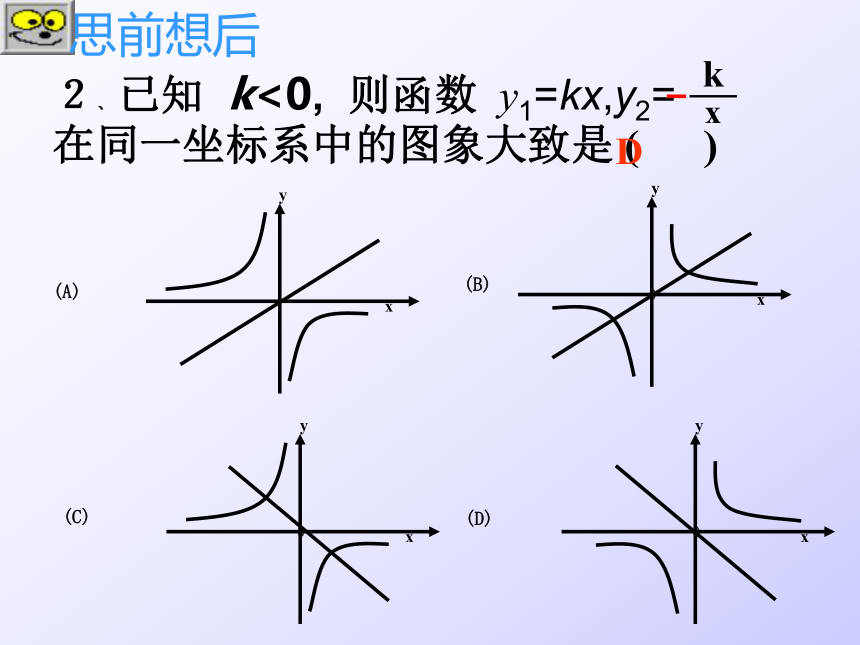
2﹑已知 k<0, 则函数 y1=kx,y2= 在同一坐标系中的图象大致是 ( )
x
k
y
x
y
0
x
x
y
0
x
y
0
(A)
(B)
(C)
(D)
D
思前想后
1.函数y= 的图象在第________象限,
在每一象限内,Y 随x 的增大而_________.
2. 函数y= 的图象在第________象限,
在每一象限内,Y 随x 的增大而_________.
3. 函数y=—— ,当x>0时,图象在第____象限,
Y 随x 的增大而_________.
4
x
- 4
x
x
5
一、三
二、四
一
减小
增大
减小
当堂训练
4.下列函数中,图象位于第二、四象限的有 ;在图象所在象限内,y的值随x的增大而增大的有 .
(3)、(4)
(2)、(3)、(5)
(A)y=5x
(B)y=2x+3
(C)
(D)
2、如图,这是下列四个函数中哪一个函数的图象
练一练
2
已知反比例函数
若函数的图象位于第一三象限,
则k_____________;
若在每一象限内,y随x增大而增大,
则k_____________.
< 4
> 4
如图,函数y=k/x和y=-kx+1(k≠0)在同一坐标系内的图象大致是 ( )
B
A
C
D
D
先假设某个函数
图象已经画好,
再确定另外的是否
符合条件.
函数y=kx-k 与 在同一条直角坐标系中的 图象可能是 :
x
y
o
x
y
o
x
y
o
x
y
o
(A) (B) (C) (D)
练一练
3
D
已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象分布在哪些象限?y随x的增大如何变化?
(2)点B(3,4) 、C(-2.5,-4.8)和D(2,5)是否在这个函数的图象上?
1.反比例函数 y= 的图象过点(-4,-2),
那么它的解析式为________.当x=1时,
y=____.
2.已知点A(-3,a),B(-2,b),在双曲线 y=- 上,则 a___b(填>、=或<)。
y=
8
x
8
当堂训练1
2
x
<
例4:图是反比例函数y= 的图象的一支.根据图象回答下列问题:
图象的另一支在哪个象限?常数m的取值范围是什么?
在这个函数图象的某一支上任取点A(a,b)和点B(a’,b’).如果a﹥a’,那么b和b’有怎么的大小关系?
m-5
x
x
y
0
a
a’
b’
b
A
B
1.已知点A(-2,y1),B(-1,y2)
都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .
y1> y2
2.已知点A(-2,y1),B(-1,y2)
都在反比例函数 的图象上,则y1与
y2的大小关系(从大到小)为 .
(k<0)
y2> y1
3.已知点
都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .
(k<0)
A(x1,y1),B(x2,y2)且x1<0<x2
y
x
o
x1
x2
A
y1
y2
B
y1 >0>y2
考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .
练一练
4
-1
-1X<-2或x>0
练一练
5
若点(-2,y1)、(-1,y2)、(2,y3)在
反比例函数 的图象上,则( )
A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1
B
反比例函数的性质
1.当k>0时,图象的两个分支分别在第一、三象限内,在每一个象限内,y随x的增大而减小;
2.当k<0时,图象的两个分支分别在第二、四象限内,在每一个象限内,y随x的增大而增大。
x
y
0
y
x
y
0
函数
正比例函数
反比例函数
解析式
图象形状
K>0
K<0
位置
增减性
位置
增减性
y=kx ( k≠0 的常数)
( k≠0的常数 )
y =
x
k
直线
双曲线
一三象限
y随x的增大而增大
一三象限
二四象限
y随x的增大而减小
在每个象限内, y随x的增大而增大
比较正比例函数和反比例函数的区别
二四象限
在每个象限内,y随x的增大而减小
2.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .
x
y
o
M
N
p
4.已知点
都在反比例函数 的图象上,则y1、y2与y3的大小关系(从大到小)为 .
A(-2,y1),B(-1,y2),C(4,y3)
y
x
o
-1
y1
y2
A
B
-2
4
C
y3
y3 >y1>y2
练 习 3
1. 已知k<0,则函数 y1=kx,y2= 在同一坐标系中的图象大致是 ( )
x
k
2. 已知k>0,则函数 y1=kx+k与y2= 在同一坐标系中
的图象大致是 ( )
x
k
3.设x为一切实数,在下列函数中,当x减小时,y的值总是增大的函数是( )
(A) y = -5x -1 ( B)y =
(C)y= -2x+2; (D)y=4x.
2
x
x
y
0
x
y
0
x
y
0
x
y
0
(A)
(B)
(C)
(D)
(A)
x
y
0
x
y
0
(B)
(C)
(D)
x
y
0
x
y
0
D
C
C
数缺形时少直觉,形少数时难入微.
已知一次函数y=kx+b(k≠0)的图象是
反比例函数 (k≠0)的图象是什么呢?
让我们一起画个反比例函数的图象看看,好吗?
“预见性”,猜一猜
反比例函数的图象又会是什么样子呢?
你还记得作函数图象的一般步骤吗?
给反比例函数“照相”
用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线(按自变量从小到大的顺序,用一条平滑的曲线连接起来).
x
画出反比例函数 和
的函数图象。
y =
x
6
y =
x
6
函数图象画法
列
表
描
点
连
线
y =
x
6
y =
x
6
描点法
注意:①列表时自变量
取值要均匀和对称②x≠0
③选整数较好计算和描点。
操作一:
1
2
3
4
5
6
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y =
x
6
y =-
x
6
-6
x
y
请大家仔细观察反比例函数
和 的函数
图象,找找看,他们有什么共同
的特征?
再让我们仔细看看,这两个
函数图象在位置上有什么关系?
操作二:
比一比:
同桌两人分别画出函数 或
的图象,看谁画得又快又好.
找一找:
1、这几个函数图象有什么共同点?
2、函数图象分别位于哪几个象限?
3、y随x的变化有怎样的变化?
根据大家所画出的函数图象,从以下几个方面出发,你
能发现反比例函数 的图象及性质有哪些?
1
2
3
4
5
6
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y =
x
6
y =-
x
6
X
y
1、这几个函数图象有什么共同点?
2、函数图象分别位于哪几个象限?
3、y随的x变化有怎样的变化?
提示:
由两支曲线组成的.因此称它的图象为双曲线;
当k>0时,两支双曲线分别位于第一,三象限内;
当k<0时,两支双曲线分别位于第二,四象限内;
当k>0时,在每一象限内,y随x的增大而减小;
当k<0时,在每一象限内,y随x的增大而增大.
反比例函数的图象无限接近于x,y轴,但永远不能到达x,y轴
⑴反比例函数的图象是轴对称图形.直线y=x和y=-x都是它的对称轴;
⑵反比例函数 与 的图象关于x轴对称,也关于y轴对称。
反比例函数的图象和性质
形状
位置
增减性
图象的发展趋势
对称性
A:
x
y
o
B:
x
y
o
D:
x
y
o
C:
x
y
o
1、反比例函数y= - 的图象大致是( )
D
函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
函数 ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三
二、四
一
减小
增大
减小
2.若关于x,y的函数 图象位于第一、三象限,
则k的取值范围是_______________
k>-1
3.甲乙两地相距100km,一辆汽车从甲地开往乙地,
把汽车到达乙地所用的时间y(h)表示为汽车的平均
速度x(km/h)的函数,则这个函数的图象大致是( )
C
2﹑已知 k<0, 则函数 y1=kx,y2= 在同一坐标系中的图象大致是 ( )
x
k
y
x
y
0
x
x
y
0
x
y
0
(A)
(B)
(C)
(D)
D
思前想后
1.函数y= 的图象在第________象限,
在每一象限内,Y 随x 的增大而_________.
2. 函数y= 的图象在第________象限,
在每一象限内,Y 随x 的增大而_________.
3. 函数y=—— ,当x>0时,图象在第____象限,
Y 随x 的增大而_________.
4
x
- 4
x
x
5
一、三
二、四
一
减小
增大
减小
当堂训练
4.下列函数中,图象位于第二、四象限的有 ;在图象所在象限内,y的值随x的增大而增大的有 .
(3)、(4)
(2)、(3)、(5)
(A)y=5x
(B)y=2x+3
(C)
(D)
2、如图,这是下列四个函数中哪一个函数的图象
练一练
2
已知反比例函数
若函数的图象位于第一三象限,
则k_____________;
若在每一象限内,y随x增大而增大,
则k_____________.
< 4
> 4
如图,函数y=k/x和y=-kx+1(k≠0)在同一坐标系内的图象大致是 ( )
B
A
C
D
D
先假设某个函数
图象已经画好,
再确定另外的是否
符合条件.
函数y=kx-k 与 在同一条直角坐标系中的 图象可能是 :
x
y
o
x
y
o
x
y
o
x
y
o
(A) (B) (C) (D)
练一练
3
D
已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象分布在哪些象限?y随x的增大如何变化?
(2)点B(3,4) 、C(-2.5,-4.8)和D(2,5)是否在这个函数的图象上?
1.反比例函数 y= 的图象过点(-4,-2),
那么它的解析式为________.当x=1时,
y=____.
2.已知点A(-3,a),B(-2,b),在双曲线 y=- 上,则 a___b(填>、=或<)。
y=
8
x
8
当堂训练1
2
x
<
例4:图是反比例函数y= 的图象的一支.根据图象回答下列问题:
图象的另一支在哪个象限?常数m的取值范围是什么?
在这个函数图象的某一支上任取点A(a,b)和点B(a’,b’).如果a﹥a’,那么b和b’有怎么的大小关系?
m-5
x
x
y
0
a
a’
b’
b
A
B
1.已知点A(-2,y1),B(-1,y2)
都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .
y1> y2
2.已知点A(-2,y1),B(-1,y2)
都在反比例函数 的图象上,则y1与
y2的大小关系(从大到小)为 .
(k<0)
y2> y1
3.已知点
都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .
(k<0)
A(x1,y1),B(x2,y2)且x1<0<x2
y
x
o
x1
x2
A
y1
y2
B
y1 >0>y2
考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .
练一练
4
-1
-1
练一练
5
若点(-2,y1)、(-1,y2)、(2,y3)在
反比例函数 的图象上,则( )
A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1
B
反比例函数的性质
1.当k>0时,图象的两个分支分别在第一、三象限内,在每一个象限内,y随x的增大而减小;
2.当k<0时,图象的两个分支分别在第二、四象限内,在每一个象限内,y随x的增大而增大。
x
y
0
y
x
y
0
函数
正比例函数
反比例函数
解析式
图象形状
K>0
K<0
位置
增减性
位置
增减性
y=kx ( k≠0 的常数)
( k≠0的常数 )
y =
x
k
直线
双曲线
一三象限
y随x的增大而增大
一三象限
二四象限
y随x的增大而减小
在每个象限内, y随x的增大而增大
比较正比例函数和反比例函数的区别
二四象限
在每个象限内,y随x的增大而减小
2.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .
x
y
o
M
N
p
4.已知点
都在反比例函数 的图象上,则y1、y2与y3的大小关系(从大到小)为 .
A(-2,y1),B(-1,y2),C(4,y3)
y
x
o
-1
y1
y2
A
B
-2
4
C
y3
y3 >y1>y2
练 习 3
1. 已知k<0,则函数 y1=kx,y2= 在同一坐标系中的图象大致是 ( )
x
k
2. 已知k>0,则函数 y1=kx+k与y2= 在同一坐标系中
的图象大致是 ( )
x
k
3.设x为一切实数,在下列函数中,当x减小时,y的值总是增大的函数是( )
(A) y = -5x -1 ( B)y =
(C)y= -2x+2; (D)y=4x.
2
x
x
y
0
x
y
0
x
y
0
x
y
0
(A)
(B)
(C)
(D)
(A)
x
y
0
x
y
0
(B)
(C)
(D)
x
y
0
x
y
0
D
C
C
