人教版数学七年级上册3.2方 程的应用课件(共26张ppt)
文档属性
| 名称 | 人教版数学七年级上册3.2方 程的应用课件(共26张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
3.2方程的应用
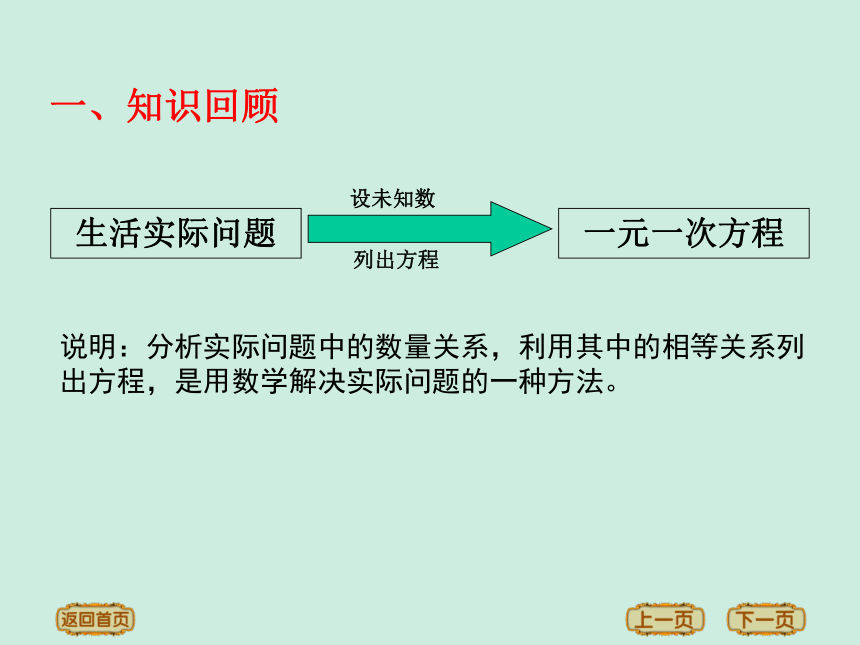
一、知识回顾
生活实际问题
设未知数
列出方程
一元一次方程
说明:分析实际问题中的数量关系,利用其中的相等关系列出方程,是用数学解决实际问题的一种方法。
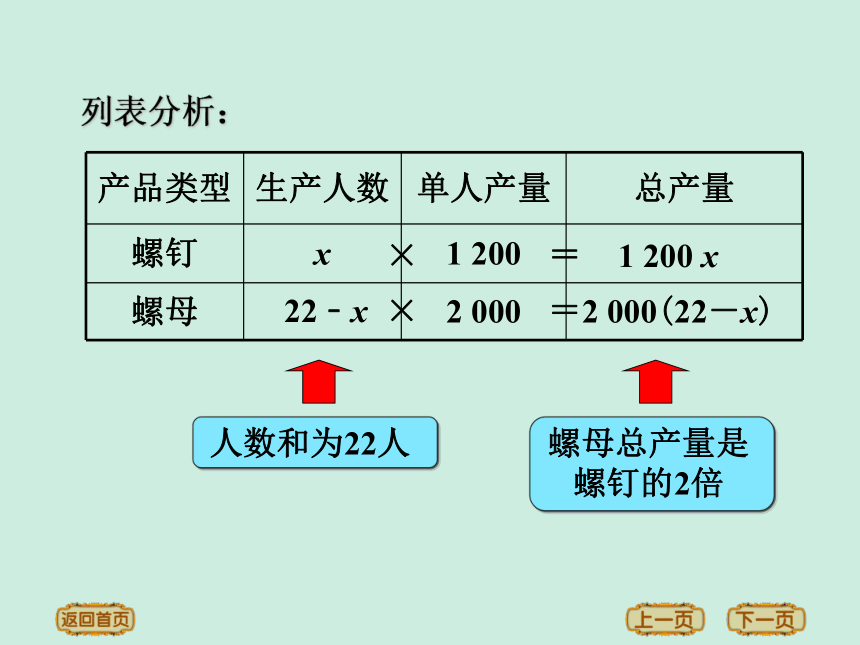
例1 某车间有22名工人,每人每天可以生产
1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
二、解决实际问题的一般过程(配套问题)
列表分析:
产品类型 生产人数 单人产量 总产量
螺钉 x 1 200
螺母 2 000
×
=
1 200 x
×
=
2 000(22-x)
人数和为22人
22﹣x
螺母总产量是螺钉的2倍
解:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
依题意得: 2 000(22-x)=2×1 200x .
解方程,得:5(22-x)=6x,
110-5x=6x,
x=10.
22-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
例2 整理一批图书,由一个人做要40 h 完成.现计划由一部分人先做4 h,然后增加 2人与他们一起做8 h,完成这项工作. 假设这些人的工作效率相同,具体应该安排多少人工作?
二、解决实际问题的一般过程(工程问题)
解:设安排 x 人先做4 h.
依题意得:
解方程,得:4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2.
答:应先安排 2人做4 h.
列一元一次方程解决实际问题一般步骤
(1)设未知数;
(2)列方程;
(3)解方程;
(4)检验;
(5)写答案.
三、归纳
1.有人问老师班级有多少名学生时,老师说:“一半学生在学数学,四分之一学生在学音乐,七分之一的学生在读外语,还剩六名学生在操场踢球.”你知道这个班有多少名学生吗?
四、巩固训练
解:设这个班有x名学生,则
答:这个班有学生56人.
探究一:销售中的盈亏
某商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
¥60元
¥60元
五、解决实际问题的探究
下面是小明同学的估算过程,你认为正确吗?
设盈利25%的衣服的进价为x元(因为是盈利,所以x<60),则这件衣服赚25%x元 , 即利润为25%x
设亏损25%的衣服的进价为y元(因为是亏损,所以y>60),则这件衣服亏25%y元,即利润为 -25%y
∵25%x<25%y(即亏的钱多于赚的钱)
25%x+ (- 25%y) <0
∴两件衣服总的是亏损
分析
(1)一件衣服的售价是60元,它的利润率是25%,它的进价是多少元?
(2)另一件衣服的售价也是60元,它的利润率是 - 25%,它的进价又是多少元?
进价 利润率 利润 售价
25% 60
进价 利润率 利润 售价
-25% 60
x
25%x
y
-25%y
解:设盈利25%的衣服的进价为x元
x+0.25x=60
设亏损25%的衣服的进价为y元
y-0.25y=60
两件衣服的进价(和)是x+y= 元。
∵进价>售价
∴卖这两件衣服总的是亏损。
现在我们来通过计算,检验你的判断是否正确吧!
它的商品利润
是 元
它的商品利润
是 元
0.25x
-0.25y
由此得x=48
由此得y=80
128
两件衣服的售价(和) 元
120
进价+利润=售价
练习:一件服装先将进价提高25%出售,后进行促销活动,又按标价的8折出售, 此时售价为60元. 请问商家是盈是亏,还是不盈不亏?
设:这件衣服的进价是x元,
则提价后的售价是(1+25%)x 元,
促销后的售价是(1+25%)x×0.8 元,
依题意得(1+25%)x×0.8=60
解得 x=60.
探究 : 球赛积分表问题
队名 比赛
场次 胜
场 负
场 积
分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
问题1:你能从表格中了解到哪些信息?
某次篮球联赛积分榜如下:
某次篮球联赛积分榜如下:
问题2:你能从表格中看出负一场积多少分吗?
队名 比赛
场次 胜
场 负
场 积
分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
负一场积1分
某次篮球联赛积分榜如下:
问题3:你能进一步算出胜一场积多少分吗?
队名 比赛
场次 胜
场 负
场 积
分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
设:胜一场积 x 分,
依题意,得
10x+1×4=24
解得: x=2
所以,胜一场积2分.
问题1:用式子表示总积分与胜、负场数之间的关系.
若一个队胜m场,则负(14 – m)场,
总积分为: 2m+(14 – m) = m+14
即胜m场的总积分为 m +14 分
问题2:某队的胜场总积分能等于它的负场总积分吗?
设一个队胜x场,则负(14-x)场,
依题意得: 2x=14-x
解得: x=
想一想,x 表示什么量?它可以是分数吗?由此你能得出什么结论?
探究三:电话计费问题
下表给出两种移动电话的计费方式:
月使用费/元 主叫限定时间/min 主叫超时费/(元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
(1)设一个月内用移动电话主叫为t 分(t是正整数).根据
上表,当 t 在不同时间范围内取值,列表说明按方式一和方式二
如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择
省钱的计费方式吗?
问题1:设一个月内用移动电话主叫为t 分(t是正整
数).根据表1,当 t 在不同时间范围内取值,
列表说明按方式一和方式二如何计费.
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
问题2:观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?
划算
划算
划算
练习: 利用我们在“电话计费问题”中学会的方法,探究下面的问题:
用A4纸在某誊印社复印文件,复印页数不超过
20时每页收费0.12元;复印页数超过20页时,超过
部分每页收费0.09元. 在某图书馆复印同样的文件,
不论复印多少页,每页收费0.1元. 如何根据复印的
页数选择复印的地点使总价格比较便宜?(复印
的页数不为零)
复印页数x 誊印社复印费用/元 图书馆复印费用/元
x 小于20 0.12x 0.1x
x 等于20 0.12×20=2.4 0.1×20=2
x 大于20 2.4+0.09(x-20) 0.1x
解:依题意列表得:
(1)当 x 小于20时,0.12 x大于0.1 x恒成立,
图书馆价格便宜;
(2)当 x 等于20时,2.4大于2,图书馆价格
便宜;
(3)当 x 大于20时,
依题意得:2.4+0.09(x-20)=0.1x
解得: x=60
∴ 当x大于20且小于60时,图书馆价格便宜;
当x大于60时,誊印社价格便宜.
综上所述:当x小于60页时,图书馆价格便宜;
当x大于60时,誊印社价格便宜.
1.谈谈用一元一次方程分析和解决实际问题
的一般过程.
2.对一些等量关系比较隐蔽的实际问题怎样去
弄清题意和数量关系.
六、课堂小结
3.2方程的应用
一、知识回顾
生活实际问题
设未知数
列出方程
一元一次方程
说明:分析实际问题中的数量关系,利用其中的相等关系列出方程,是用数学解决实际问题的一种方法。
例1 某车间有22名工人,每人每天可以生产
1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
二、解决实际问题的一般过程(配套问题)
列表分析:
产品类型 生产人数 单人产量 总产量
螺钉 x 1 200
螺母 2 000
×
=
1 200 x
×
=
2 000(22-x)
人数和为22人
22﹣x
螺母总产量是螺钉的2倍
解:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
依题意得: 2 000(22-x)=2×1 200x .
解方程,得:5(22-x)=6x,
110-5x=6x,
x=10.
22-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
例2 整理一批图书,由一个人做要40 h 完成.现计划由一部分人先做4 h,然后增加 2人与他们一起做8 h,完成这项工作. 假设这些人的工作效率相同,具体应该安排多少人工作?
二、解决实际问题的一般过程(工程问题)
解:设安排 x 人先做4 h.
依题意得:
解方程,得:4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2.
答:应先安排 2人做4 h.
列一元一次方程解决实际问题一般步骤
(1)设未知数;
(2)列方程;
(3)解方程;
(4)检验;
(5)写答案.
三、归纳
1.有人问老师班级有多少名学生时,老师说:“一半学生在学数学,四分之一学生在学音乐,七分之一的学生在读外语,还剩六名学生在操场踢球.”你知道这个班有多少名学生吗?
四、巩固训练
解:设这个班有x名学生,则
答:这个班有学生56人.
探究一:销售中的盈亏
某商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
¥60元
¥60元
五、解决实际问题的探究
下面是小明同学的估算过程,你认为正确吗?
设盈利25%的衣服的进价为x元(因为是盈利,所以x<60),则这件衣服赚25%x元 , 即利润为25%x
设亏损25%的衣服的进价为y元(因为是亏损,所以y>60),则这件衣服亏25%y元,即利润为 -25%y
∵25%x<25%y(即亏的钱多于赚的钱)
25%x+ (- 25%y) <0
∴两件衣服总的是亏损
分析
(1)一件衣服的售价是60元,它的利润率是25%,它的进价是多少元?
(2)另一件衣服的售价也是60元,它的利润率是 - 25%,它的进价又是多少元?
进价 利润率 利润 售价
25% 60
进价 利润率 利润 售价
-25% 60
x
25%x
y
-25%y
解:设盈利25%的衣服的进价为x元
x+0.25x=60
设亏损25%的衣服的进价为y元
y-0.25y=60
两件衣服的进价(和)是x+y= 元。
∵进价>售价
∴卖这两件衣服总的是亏损。
现在我们来通过计算,检验你的判断是否正确吧!
它的商品利润
是 元
它的商品利润
是 元
0.25x
-0.25y
由此得x=48
由此得y=80
128
两件衣服的售价(和) 元
120
进价+利润=售价
练习:一件服装先将进价提高25%出售,后进行促销活动,又按标价的8折出售, 此时售价为60元. 请问商家是盈是亏,还是不盈不亏?
设:这件衣服的进价是x元,
则提价后的售价是(1+25%)x 元,
促销后的售价是(1+25%)x×0.8 元,
依题意得(1+25%)x×0.8=60
解得 x=60.
探究 : 球赛积分表问题
队名 比赛
场次 胜
场 负
场 积
分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
问题1:你能从表格中了解到哪些信息?
某次篮球联赛积分榜如下:
某次篮球联赛积分榜如下:
问题2:你能从表格中看出负一场积多少分吗?
队名 比赛
场次 胜
场 负
场 积
分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
负一场积1分
某次篮球联赛积分榜如下:
问题3:你能进一步算出胜一场积多少分吗?
队名 比赛
场次 胜
场 负
场 积
分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
设:胜一场积 x 分,
依题意,得
10x+1×4=24
解得: x=2
所以,胜一场积2分.
问题1:用式子表示总积分与胜、负场数之间的关系.
若一个队胜m场,则负(14 – m)场,
总积分为: 2m+(14 – m) = m+14
即胜m场的总积分为 m +14 分
问题2:某队的胜场总积分能等于它的负场总积分吗?
设一个队胜x场,则负(14-x)场,
依题意得: 2x=14-x
解得: x=
想一想,x 表示什么量?它可以是分数吗?由此你能得出什么结论?
探究三:电话计费问题
下表给出两种移动电话的计费方式:
月使用费/元 主叫限定时间/min 主叫超时费/(元/min) 被叫
方式一 58 150 0.25 免费
方式二 88 350 0.19 免费
(1)设一个月内用移动电话主叫为t 分(t是正整数).根据
上表,当 t 在不同时间范围内取值,列表说明按方式一和方式二
如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择
省钱的计费方式吗?
问题1:设一个月内用移动电话主叫为t 分(t是正整
数).根据表1,当 t 在不同时间范围内取值,
列表说明按方式一和方式二如何计费.
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
问题2:观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?
划算
划算
划算
练习: 利用我们在“电话计费问题”中学会的方法,探究下面的问题:
用A4纸在某誊印社复印文件,复印页数不超过
20时每页收费0.12元;复印页数超过20页时,超过
部分每页收费0.09元. 在某图书馆复印同样的文件,
不论复印多少页,每页收费0.1元. 如何根据复印的
页数选择复印的地点使总价格比较便宜?(复印
的页数不为零)
复印页数x 誊印社复印费用/元 图书馆复印费用/元
x 小于20 0.12x 0.1x
x 等于20 0.12×20=2.4 0.1×20=2
x 大于20 2.4+0.09(x-20) 0.1x
解:依题意列表得:
(1)当 x 小于20时,0.12 x大于0.1 x恒成立,
图书馆价格便宜;
(2)当 x 等于20时,2.4大于2,图书馆价格
便宜;
(3)当 x 大于20时,
依题意得:2.4+0.09(x-20)=0.1x
解得: x=60
∴ 当x大于20且小于60时,图书馆价格便宜;
当x大于60时,誊印社价格便宜.
综上所述:当x小于60页时,图书馆价格便宜;
当x大于60时,誊印社价格便宜.
1.谈谈用一元一次方程分析和解决实际问题
的一般过程.
2.对一些等量关系比较隐蔽的实际问题怎样去
弄清题意和数量关系.
六、课堂小结
