人教版数学七年级上册4.3角(共28张ppt)
文档属性
| 名称 | 人教版数学七年级上册4.3角(共28张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 06:41:35 | ||
图片预览







文档简介
你能描述这些角的共同特征吗?
1、
角是由两条具有公共端点的射线组成的.
两条射线的公共端点是这个角的顶点.
两条射线是这个角的两条边.
角的另一种定义
2.角也可以看成是由一条射线
绕着它的端点旋转而成的。
一条射线绕着它的端点旋转,
当终边和始边成一条直线时,所成
的角叫做平角。
继续旋转,当终边和始边重
合时,所成的角叫做周角。
1周角=3600
1平角=1800
O
始边
终边
A
B
O
O
A(B)
注意:
(1)角的大小与画出的角的边的长短无关,只与两边张开的程度有关;
(2)平角不是直线,可以说平角的两边成一条直线;平角有顶点,有边,直线无;
角的表示方法:
(1)用三个大写字母;如∠ABC;
(2)用一个大写字母,如∠A,前提顶点只有一个角
(3)用一个数字,如∠1;
(4)用一个希腊字母,如∠α。
B
A
C
B
A
D
C
⑴
⑵
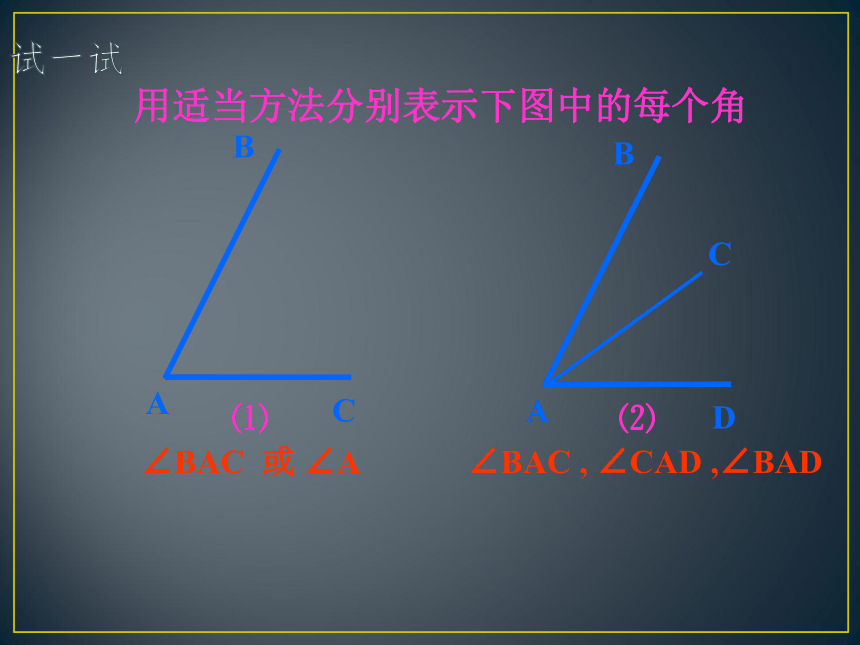
用适当方法分别表示下图中的每个角
∠BAC 或 ∠A
∠BAC , ∠CAD ,∠BAD
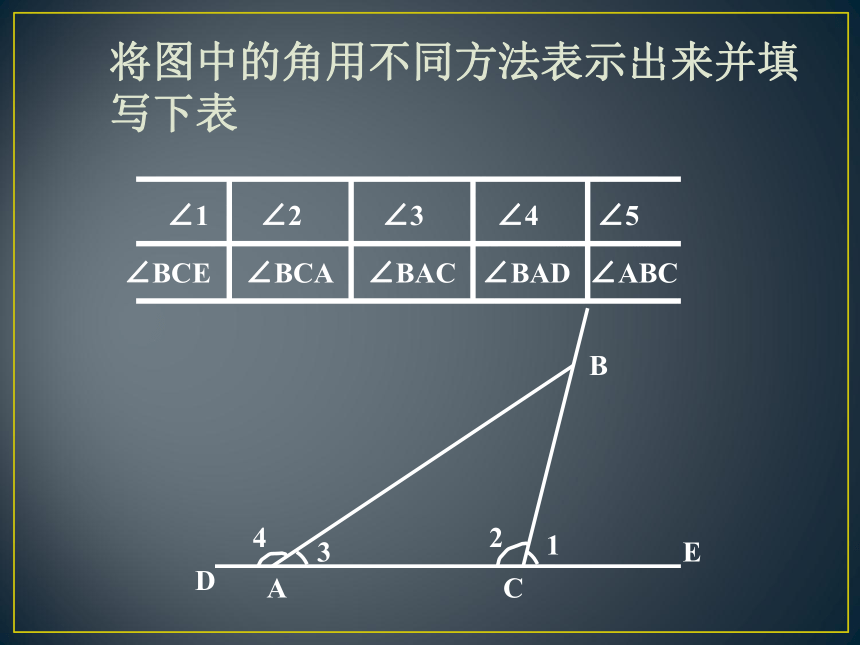
∠2
∠5
∠BCE
∠BAD
∠BAC
∠1
∠3
∠4
∠ABC
∠BCA
2
1
3
4
B
A
D
C
E
将图中的角用不同方法表示出来并填写下表
⑴请用字母表示图中的每个城市.
⑵请用字母分别表示以北京为中心的每两个城市之间的夹角.
⑶请用量角器测量出上述夹角的度数.
A
B
C
D
.
.
.
.
.
O
方向角:方向角指的是在某观测点,观察某物体在该观测点的某个方向的角。一般的方向角都以观测点的正北,正南为基础以 偏西或偏东的角度来描述。如北偏东30°就是从观测点先指向北,再向东偏转30°
练一练
1、如图1, D、E分别是AB、AC上的点.
∠ ABC与∠ DBC是不是同一个角?
∠BAC与∠ DAE是不是同一个角?
∠BAC与∠ ACB是不是同一个角?
2、如图2, ∠ AOE内部引三条射线,图中共有多少个角?如果引出99条射线,有多少个角呢?n条射线有多少个角?
D
E
A
C
B
图1
O
A
D
E
C
B
图2
3、如图3,用大写字母表示图中用希腊字母标注的角。
∠ α =___ ∠ β=____
∠ γ =___ ∠ θ=_____
A
C
B
图3
D
E
F
γ
β
α
θ
1°的 为1分,
1
60
记作“1′”
即1°=60′.
1′的 为1秒,
1
60
记作“1″”
即1′=60″.
back
计算:
⑴1.45°等于多少分? 等于多少秒?
⑵1800″等于多少分? 等于多少度?
解: ⑴ 60′× 1.45
=87′,
即 1.45°=87′=5220″.
⑵( ) ′× 1800=
1
60
30′,
60″× 87
=5220″,
( ) ° × 30 =
1
60
0.5°,
即 1800″=30′=0.5°.
0.25°等于多少分? 等于多少秒?
解:60′× 0.25 = 15′
60″× 15 = 900″
即0.25°= 15′= 900″.
2700″等于多少分? 等于多少度?
解:
( ) ′ × 2700 =45′
( ) °× 45 =0.75°
即2700″=45′=0.75°.
1
60
1
60
1
8
(
) °等于多少分? 等于多少秒?
1
8
解: 60′× =7.5′
60″× 7.5 =450″
即( ) °=7.5′=450″.
1
8
6000″等于多少分? 等于多少度?
( ) ′ × 6000 =100′
( ) ° × 100 = ( )°
即6000″=45′= ( )°.
1
60
解:
1
60
5
3
5
3
确定相应钟表上时针与分针所成的角度
120°
Back
30°
Back
120°
Back
90°
Back
0°或360°或720°
1、每经过1小时,时针转过多少度?
每经过1分钟,分针转过多少度?
问题
30°
6°
2.钟表指示8时,时针与分针成多少度角?8时30分时,时针与分针成多少度角?8时45分时,时针与分针夹角是多少度? 8时51分时,时针与分针夹角是多少度?
答案:120°;75°;7.5°; 40.5°
1.角的概念
2.角的表示方法有四种:用三个大写字母表示;用一个大写字母表示;用一个希腊字母或一个阿拉伯数字表示.
3.角的单位及其换算.
1、
角是由两条具有公共端点的射线组成的.
两条射线的公共端点是这个角的顶点.
两条射线是这个角的两条边.
角的另一种定义
2.角也可以看成是由一条射线
绕着它的端点旋转而成的。
一条射线绕着它的端点旋转,
当终边和始边成一条直线时,所成
的角叫做平角。
继续旋转,当终边和始边重
合时,所成的角叫做周角。
1周角=3600
1平角=1800
O
始边
终边
A
B
O
O
A(B)
注意:
(1)角的大小与画出的角的边的长短无关,只与两边张开的程度有关;
(2)平角不是直线,可以说平角的两边成一条直线;平角有顶点,有边,直线无;
角的表示方法:
(1)用三个大写字母;如∠ABC;
(2)用一个大写字母,如∠A,前提顶点只有一个角
(3)用一个数字,如∠1;
(4)用一个希腊字母,如∠α。
B
A
C
B
A
D
C
⑴
⑵
用适当方法分别表示下图中的每个角
∠BAC 或 ∠A
∠BAC , ∠CAD ,∠BAD
∠2
∠5
∠BCE
∠BAD
∠BAC
∠1
∠3
∠4
∠ABC
∠BCA
2
1
3
4
B
A
D
C
E
将图中的角用不同方法表示出来并填写下表
⑴请用字母表示图中的每个城市.
⑵请用字母分别表示以北京为中心的每两个城市之间的夹角.
⑶请用量角器测量出上述夹角的度数.
A
B
C
D
.
.
.
.
.
O
方向角:方向角指的是在某观测点,观察某物体在该观测点的某个方向的角。一般的方向角都以观测点的正北,正南为基础以 偏西或偏东的角度来描述。如北偏东30°就是从观测点先指向北,再向东偏转30°
练一练
1、如图1, D、E分别是AB、AC上的点.
∠ ABC与∠ DBC是不是同一个角?
∠BAC与∠ DAE是不是同一个角?
∠BAC与∠ ACB是不是同一个角?
2、如图2, ∠ AOE内部引三条射线,图中共有多少个角?如果引出99条射线,有多少个角呢?n条射线有多少个角?
D
E
A
C
B
图1
O
A
D
E
C
B
图2
3、如图3,用大写字母表示图中用希腊字母标注的角。
∠ α =___ ∠ β=____
∠ γ =___ ∠ θ=_____
A
C
B
图3
D
E
F
γ
β
α
θ
1°的 为1分,
1
60
记作“1′”
即1°=60′.
1′的 为1秒,
1
60
记作“1″”
即1′=60″.
back
计算:
⑴1.45°等于多少分? 等于多少秒?
⑵1800″等于多少分? 等于多少度?
解: ⑴ 60′× 1.45
=87′,
即 1.45°=87′=5220″.
⑵( ) ′× 1800=
1
60
30′,
60″× 87
=5220″,
( ) ° × 30 =
1
60
0.5°,
即 1800″=30′=0.5°.
0.25°等于多少分? 等于多少秒?
解:60′× 0.25 = 15′
60″× 15 = 900″
即0.25°= 15′= 900″.
2700″等于多少分? 等于多少度?
解:
( ) ′ × 2700 =45′
( ) °× 45 =0.75°
即2700″=45′=0.75°.
1
60
1
60
1
8
(
) °等于多少分? 等于多少秒?
1
8
解: 60′× =7.5′
60″× 7.5 =450″
即( ) °=7.5′=450″.
1
8
6000″等于多少分? 等于多少度?
( ) ′ × 6000 =100′
( ) ° × 100 = ( )°
即6000″=45′= ( )°.
1
60
解:
1
60
5
3
5
3
确定相应钟表上时针与分针所成的角度
120°
Back
30°
Back
120°
Back
90°
Back
0°或360°或720°
1、每经过1小时,时针转过多少度?
每经过1分钟,分针转过多少度?
问题
30°
6°
2.钟表指示8时,时针与分针成多少度角?8时30分时,时针与分针成多少度角?8时45分时,时针与分针夹角是多少度? 8时51分时,时针与分针夹角是多少度?
答案:120°;75°;7.5°; 40.5°
1.角的概念
2.角的表示方法有四种:用三个大写字母表示;用一个大写字母表示;用一个希腊字母或一个阿拉伯数字表示.
3.角的单位及其换算.
