湘教版(2012)初中数学八年级上册 小结练习 3 实数 总复习 课件(共19张ppt)
文档属性
| 名称 | 湘教版(2012)初中数学八年级上册 小结练习 3 实数 总复习 课件(共19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览





文档简介
湘教版 SHUXUE 八年级上
本节内容
第三章
1.平方根的定义:
如果有一个数r,使得r2=a,那么我们把r叫作
a的一个平方根,也叫作二次方根.
符号表示为:若 r2= a ;r= .
2.平方根的性质:
(1)一个正数有2个平方根,它们互为相反数;
(2)0的平方根是0;
(3)负数没有平方根。
3.算术平方根的定义:
我们把正数a的正平方根叫做算术平方根。
4.算术平方根的性质:
一个非负数的算术平方根是非负数。
一个数的算术平方根的平方等于这个数本身。
一个数的平方的算术平方根等于这个数的绝对值。
-
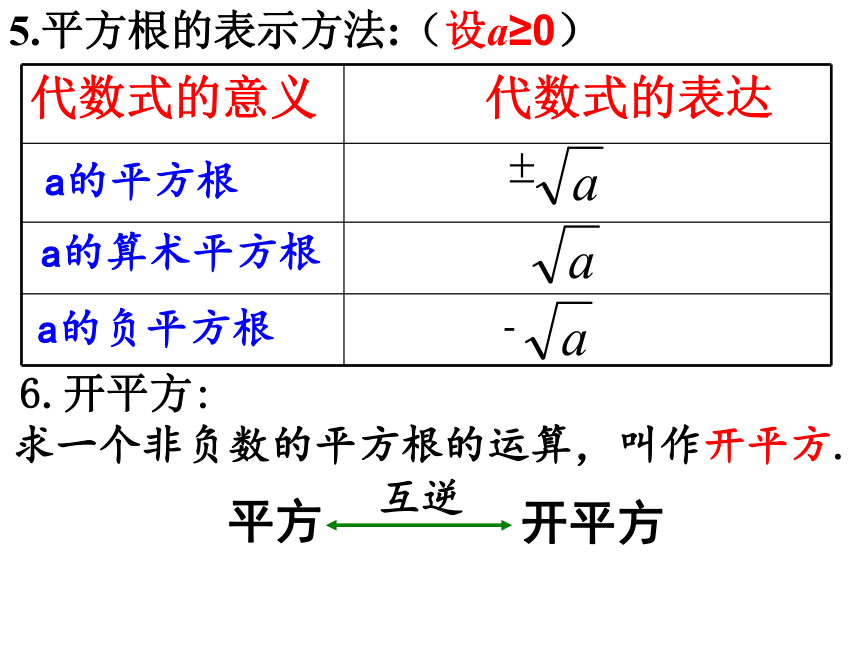
代数式的意义
代数式的表达
a的算术平方根
a的负平方根
a的平方根
5.平方根的表示方法:(设a≥0)
求一个非负数的平方根的运算,叫作开平方.
6.开平方:
开平方
平方
互逆
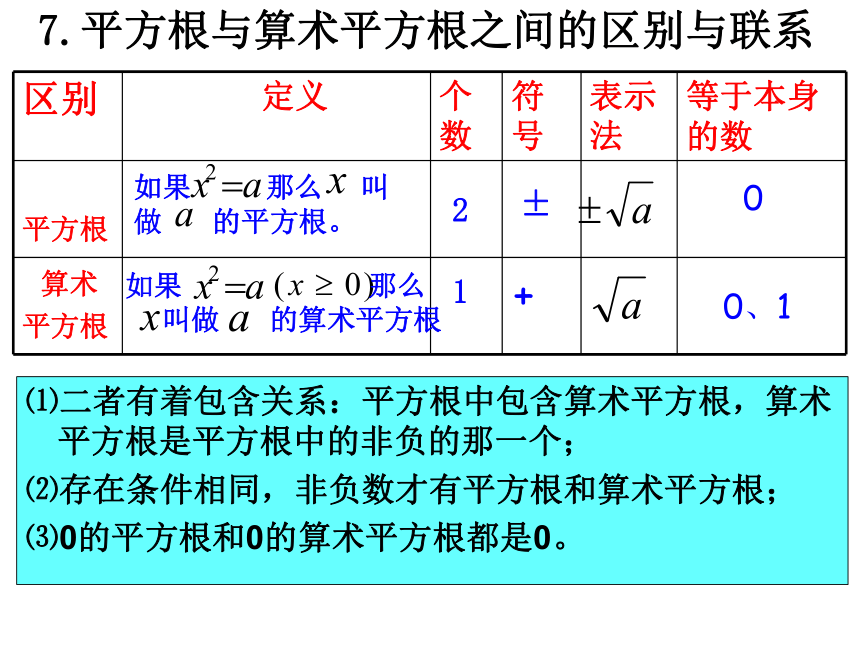
7.平方根与算术平方根之间的区别与联系
区别
定义
个数
符号
表示法
等于本身的数
平方根
算术
平方根
如果 那么 叫做 的平方根。
如果 那么
叫做 的算术平方根
1
2
±
+
0
0、1
⑴二者有着包含关系:平方根中包含算术平方根,算术平方根是平方根中的非负的那一个;
⑵存在条件相同,非负数才有平方根和算术平方根;
⑶0的平方根和0的算术平方根都是0。
即一个非负数的算术平方根是非负数。
即一个数的绝对值是非负数。
即一个数的平方是非负数。
8.非负性:
如果几个非负数相加和为0,
则这几个非负数都等于0.
课堂练习
一.求下列各式的平方根与算术平方根:
一般地,求一个数的平方根的方法有两种:
1.根据乘方意义求平方根; 2.用计算器求平方根.
1.4的平方根是 ;算术平方根是_____
±2
2
二.填空:
2.若x2=3,则 x= ,若 =3,则 x= ;
±3
3.若(x-1)2=4,则x= ,
3或-1
4.若一个数的一个平方根为-7,则另一个平方根为 ,这个数是 。
7
49
5.若一个正数的两个平方根为2a-6、3a+1,则a= ,这个正数为 ;
1
16
如果一个数b,使得b3=a,那么我们把b叫作a的一个立方根,也叫作三次方根.
a 的立方根记作 ,读作“立方根号a”或“三次根号a”.
用符号表示为:若b3=a,则b= .
9.立方根的定义:
立方根的符号与被开方数的符号相同。
(1) 一个正数有一个立方根,是正数;
(2) 0的立方根是0;
(3) 一个负数有一个立方根,是负数。
10.立方根的性质(唯一性):
一个数的立方根的立方等于这个数本身。
一个数的立方的立方根等于这个数本身。
若两个数互为相反数,那么这两个
数的立方根也互为相反数。
代数式的意义
代数式的表达
12.立方根的表示方法:
求一个数的立方根的运算,叫作开立方.
11.开立方:
开立方
立方
互逆
联系:
(1)0的平方根、立方根都是0.
(2)平方根、立方根都是开方的结果.
定义
表示法
被开方数a的取值范围
正数
0
负数
平方根
立方根
如果b3=a,那么b叫作a的一个立方根,
如果r2=a,那么r叫作a的一个平方根,
非负数
任何实数
2个
平方根
1个
平方根
无
1个
立方根
1个
立方根
1个
立方根
区别
13.平方根与立方根的区别与联系:
一.求下列各式的立方根:
课堂练习
一般地,求一个数的立方根的方法有两种:
1.根据乘方意义求立方根; 2.用计算器求立方根.
(1)平方根是它本身的数是____.
(2)算术平方根是其本身的数是__________.
(3)立方根是其本身的数是_________.
(4) 的立方根为 .
0
0,1,-1
0,1,
-2
二.求下列各式的立方根:
(5)已知y= + -3,求xy的立方根。
按定义分:
按正负分:
13.实数的分类:
实数
有理数
整数
正整数
(自然数)
零
负整数
分数
正分数
负分数
无理数
正无理数
负无理数
负无理数
负分数
负整数
负有理数
负实数
零
正无理数
正分数
正整数
正有理数
正实数
实数
(自然数)
按定义分:
按正负分:
1含有 的式子
2.开不尽方的数及化简之后含根号的数
3.一般形式的无限不循环小数。
注意:带根号的数不一定是无理数,如
例如:2+ , -3,5 ……
无限不循环小数叫做无理数(强调:无限,不循环.)
无理数常见的3种典型:
一.把下列各数填入相应的集合内:
有理数集合:
无理数集合:
整数集合:
分数集合:
实数集合:
1. 的相反数是 ,倒数是 .
2.绝对值小于 的整数是 ,
3.一个数的绝对值是 ,则这个数是 .
二.填空:
4.a、b互为相反数,c与d互为倒数,则a+1+b+cd= 。
2
5.若3,m,5为三角形三边,化简:
=2m-10
三.计算:
本节内容
第三章
1.平方根的定义:
如果有一个数r,使得r2=a,那么我们把r叫作
a的一个平方根,也叫作二次方根.
符号表示为:若 r2= a ;r= .
2.平方根的性质:
(1)一个正数有2个平方根,它们互为相反数;
(2)0的平方根是0;
(3)负数没有平方根。
3.算术平方根的定义:
我们把正数a的正平方根叫做算术平方根。
4.算术平方根的性质:
一个非负数的算术平方根是非负数。
一个数的算术平方根的平方等于这个数本身。
一个数的平方的算术平方根等于这个数的绝对值。
-
代数式的意义
代数式的表达
a的算术平方根
a的负平方根
a的平方根
5.平方根的表示方法:(设a≥0)
求一个非负数的平方根的运算,叫作开平方.
6.开平方:
开平方
平方
互逆
7.平方根与算术平方根之间的区别与联系
区别
定义
个数
符号
表示法
等于本身的数
平方根
算术
平方根
如果 那么 叫做 的平方根。
如果 那么
叫做 的算术平方根
1
2
±
+
0
0、1
⑴二者有着包含关系:平方根中包含算术平方根,算术平方根是平方根中的非负的那一个;
⑵存在条件相同,非负数才有平方根和算术平方根;
⑶0的平方根和0的算术平方根都是0。
即一个非负数的算术平方根是非负数。
即一个数的绝对值是非负数。
即一个数的平方是非负数。
8.非负性:
如果几个非负数相加和为0,
则这几个非负数都等于0.
课堂练习
一.求下列各式的平方根与算术平方根:
一般地,求一个数的平方根的方法有两种:
1.根据乘方意义求平方根; 2.用计算器求平方根.
1.4的平方根是 ;算术平方根是_____
±2
2
二.填空:
2.若x2=3,则 x= ,若 =3,则 x= ;
±3
3.若(x-1)2=4,则x= ,
3或-1
4.若一个数的一个平方根为-7,则另一个平方根为 ,这个数是 。
7
49
5.若一个正数的两个平方根为2a-6、3a+1,则a= ,这个正数为 ;
1
16
如果一个数b,使得b3=a,那么我们把b叫作a的一个立方根,也叫作三次方根.
a 的立方根记作 ,读作“立方根号a”或“三次根号a”.
用符号表示为:若b3=a,则b= .
9.立方根的定义:
立方根的符号与被开方数的符号相同。
(1) 一个正数有一个立方根,是正数;
(2) 0的立方根是0;
(3) 一个负数有一个立方根,是负数。
10.立方根的性质(唯一性):
一个数的立方根的立方等于这个数本身。
一个数的立方的立方根等于这个数本身。
若两个数互为相反数,那么这两个
数的立方根也互为相反数。
代数式的意义
代数式的表达
12.立方根的表示方法:
求一个数的立方根的运算,叫作开立方.
11.开立方:
开立方
立方
互逆
联系:
(1)0的平方根、立方根都是0.
(2)平方根、立方根都是开方的结果.
定义
表示法
被开方数a的取值范围
正数
0
负数
平方根
立方根
如果b3=a,那么b叫作a的一个立方根,
如果r2=a,那么r叫作a的一个平方根,
非负数
任何实数
2个
平方根
1个
平方根
无
1个
立方根
1个
立方根
1个
立方根
区别
13.平方根与立方根的区别与联系:
一.求下列各式的立方根:
课堂练习
一般地,求一个数的立方根的方法有两种:
1.根据乘方意义求立方根; 2.用计算器求立方根.
(1)平方根是它本身的数是____.
(2)算术平方根是其本身的数是__________.
(3)立方根是其本身的数是_________.
(4) 的立方根为 .
0
0,1,-1
0,1,
-2
二.求下列各式的立方根:
(5)已知y= + -3,求xy的立方根。
按定义分:
按正负分:
13.实数的分类:
实数
有理数
整数
正整数
(自然数)
零
负整数
分数
正分数
负分数
无理数
正无理数
负无理数
负无理数
负分数
负整数
负有理数
负实数
零
正无理数
正分数
正整数
正有理数
正实数
实数
(自然数)
按定义分:
按正负分:
1含有 的式子
2.开不尽方的数及化简之后含根号的数
3.一般形式的无限不循环小数。
注意:带根号的数不一定是无理数,如
例如:2+ , -3,5 ……
无限不循环小数叫做无理数(强调:无限,不循环.)
无理数常见的3种典型:
一.把下列各数填入相应的集合内:
有理数集合:
无理数集合:
整数集合:
分数集合:
实数集合:
1. 的相反数是 ,倒数是 .
2.绝对值小于 的整数是 ,
3.一个数的绝对值是 ,则这个数是 .
二.填空:
4.a、b互为相反数,c与d互为倒数,则a+1+b+cd= 。
2
5.若3,m,5为三角形三边,化简:
=2m-10
三.计算:
同课章节目录
