湘教版(2012)初中数学八年级上册2.1 三角形的内角与外角 课件(共23张ppt)
文档属性
| 名称 | 湘教版(2012)初中数学八年级上册2.1 三角形的内角与外角 课件(共23张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 06:46:57 | ||
图片预览





文档简介
三角形的内角与外角
1. 掌握三角形的内角和定理
2. 三角形的分类(按角分)
2. 三角形的内角与外角的关系
学习目标:
知识点一:
三角形的内角和定理
问题1:三角形有几个内角?
问题2:三角形的内角和是多少?
问题3:如何证明三角形的内角和为180度?
(小组讨论)
3个
3
2
3
1
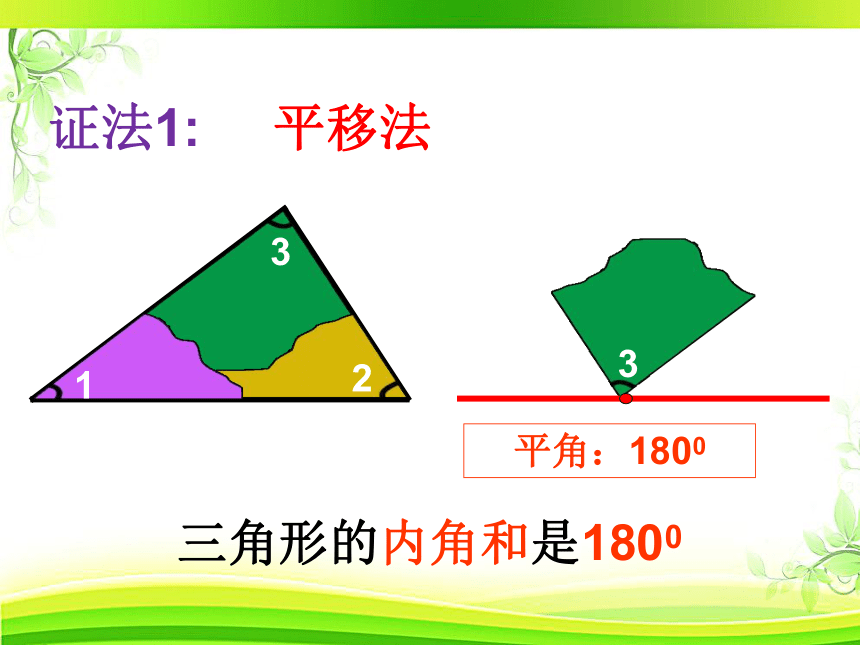
平角:1800
三角形的内角和是1800
证法1: 平移法
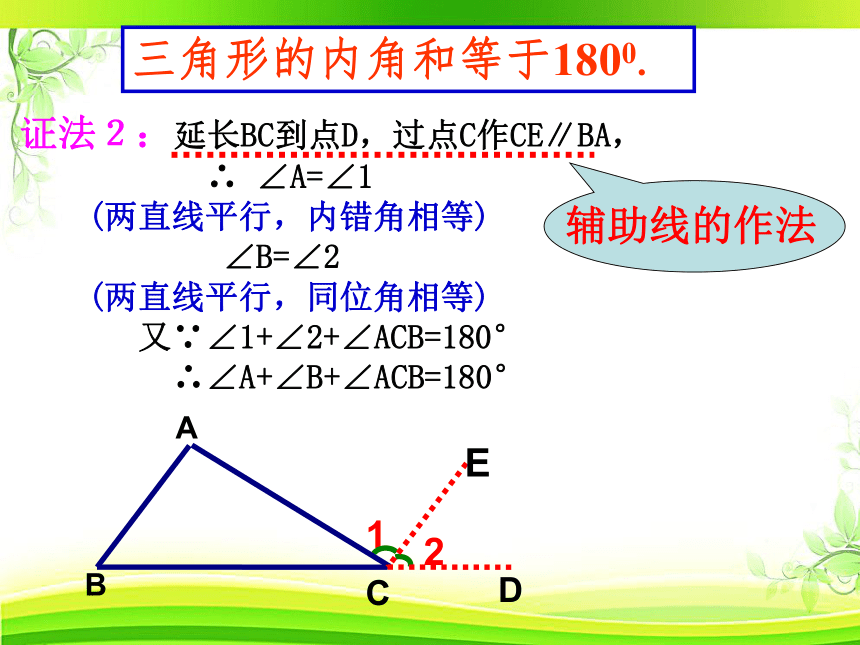
证法2:延长BC到点D,过点C作CE∥BA,
∴ ∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
2
1
E
D
C
B
A
三角形的内角和等于1800.
辅助线的作法
证法3:
C
B
E
A
三角形的内角和等于1800.
过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°
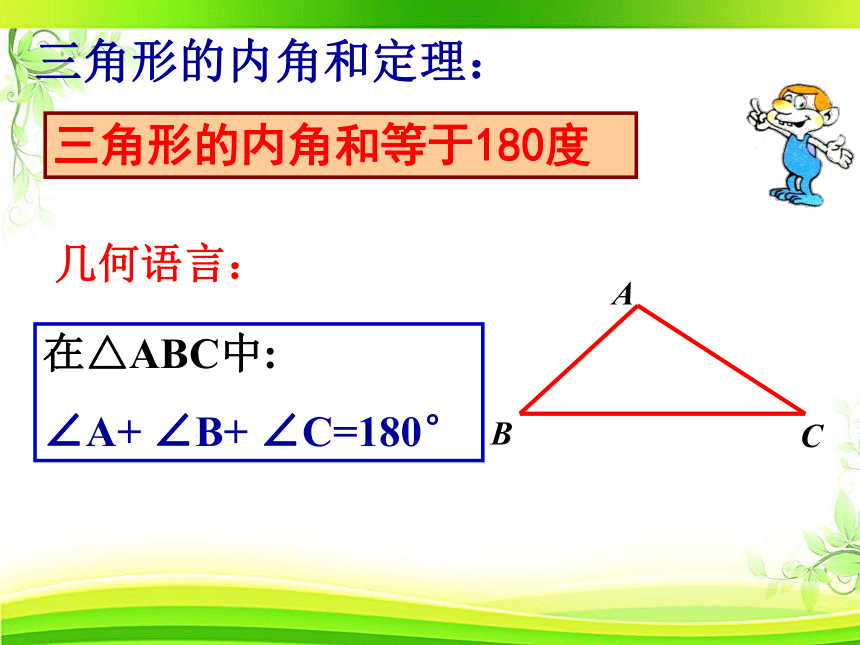
三角形的内角和定理:
三角形的内角和等于180度
A
B
C
在△ABC中:
∠A+ ∠B+ ∠C=180°
几何语言:
例1 在△ABC 中,∠A 的度数是∠B 的度数
的3倍,∠C 比∠B 大15°,求∠A,∠B,∠C
的度数.
典例精讲
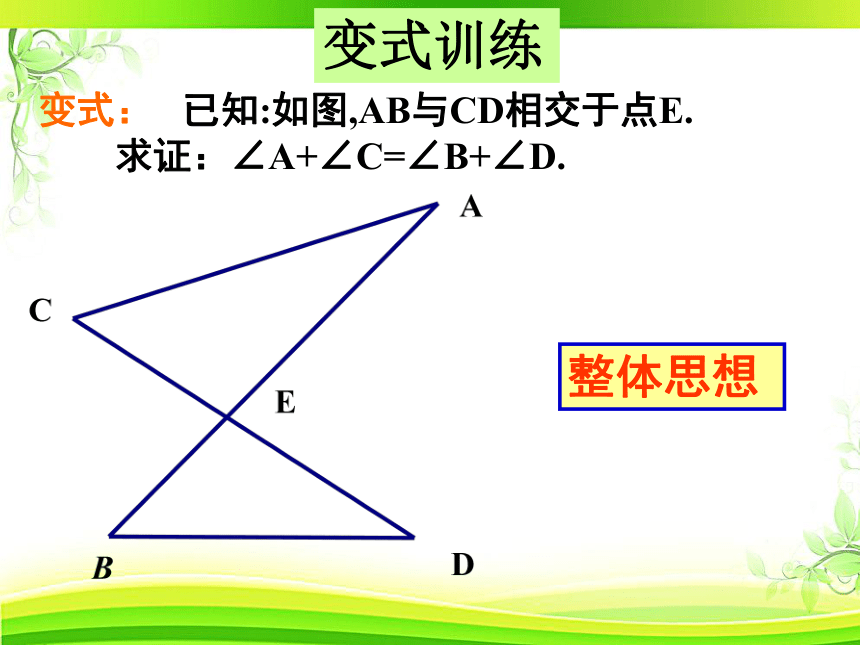
变式: 已知:如图,AB与CD相交于点E.
求证:∠A+∠C=∠B+∠D.
变式训练
整体思想
一个三角形的三个内角中, 最多有几个直角?
最多有几个钝角?
三角形的内角和等于180°,
因此最多有一个直角
或一个钝角.
七嘴八舌
知识点二:
三角形的分类
三角形按角如何分类呢?
探究
锐角三角形
直角三角形
三角形按角如何分类呢?
探究
三角形中,三个角都是锐角的三角形叫锐角三角形,
有一个角是直角的三角形叫直角三角形,
有一个角是钝角的三角形叫钝角三角形
锐角三角形
钝角三角形
直角三角形
三角形按角大小分类:
三角形
锐角三角形(三个角为锐角)
钝角三角形(一个角为钝角)
直角三角形(一个角为直角)
斜三角形
A
B
C
D
BD是AB的延长线
BC是△ ABC的边
定义:三角形的一边与另一边的延长线
所组成的角叫做三角形的外角.
你能说出∠CBD的边与△ABC的边的关系吗?
三角形的外角
相邻的
内角
不相邻的内角
不相邻的内角
三角形的外角与相邻内角互为_____。
补角
三角形的外角与不相邻的内角有什么关系?
知识点三:
三角形的内角与外角的关系
∠ACD+ ∠ACB =180°
∠A+ ∠B+ ∠ACB =180°
所以, ∠A+ ∠B= ∠ACD
解:
B
C
D
A
∵∠ACD是△ ABC的外角
∴∠ACD= ∠A+ ∠B
三角形的一个外角等于与它不相邻的两个内角的和。
几何语言:
结论:
思考:1、如何说明 ∠ACD= ∠B+ ∠ A?
思考:1、试说明 ∠ACD与 ∠B、 ∠ACD与 ∠ A的大小关系?
D
A
B
三角形的一个外角大于任何
一个不相邻的内角。
推论:
1、n=____ x=_____ y=_____
27
29
59
课堂检测
2、在△ABC中,
(1)已知∠A=80°,∠B=52°, 则∠C=__
(2)已知∠A=80°, ∠B-∠C= 40°,则∠C= __
(3)已知∠A :∠B : ∠C =1:3:5,能否求
∠A 、∠B、∠C的度数?
48°
30°
课堂检测
3、当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为_______.
课堂检测
4、如图,一个60°的角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为( )
A. 120° B. 180° C. 240° D. 300°
5、如图,∠1+∠2+∠3+∠4= ______度.
如图所示:求∠A+∠B+∠C+∠D+∠E的度数?
E
D
C
B
A
1
2
解:∵∠1= ∠A+ ∠D
(三角形的外角等于与它不相邻的两内角的和)
又∵∠2= ∠B+ ∠E
(三角形的外角等于与它不相邻的两内角的和)
∴ ∠A+∠B+∠C+∠D+∠E
=(∠A+ ∠D)+(∠B+ ∠E)+∠C
=∠1+∠2+∠C
=180°
智勇大比拼!
直角三角形可用符号“Rt△” 来表示, 例如直角三角形ABC 可以记作“Rt△ABC”.
在直角三角形中, 夹直角的两边叫作直角边,
直角的对边叫作斜边.
两条直角边相等的直角三角形叫作等腰直角三角形.
1. 掌握三角形的内角和定理
2. 三角形的分类(按角分)
2. 三角形的内角与外角的关系
学习目标:
知识点一:
三角形的内角和定理
问题1:三角形有几个内角?
问题2:三角形的内角和是多少?
问题3:如何证明三角形的内角和为180度?
(小组讨论)
3个
3
2
3
1
平角:1800
三角形的内角和是1800
证法1: 平移法
证法2:延长BC到点D,过点C作CE∥BA,
∴ ∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
2
1
E
D
C
B
A
三角形的内角和等于1800.
辅助线的作法
证法3:
C
B
E
A
三角形的内角和等于1800.
过A作AE∥BC,
∴∠B=∠BAE
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°
三角形的内角和定理:
三角形的内角和等于180度
A
B
C
在△ABC中:
∠A+ ∠B+ ∠C=180°
几何语言:
例1 在△ABC 中,∠A 的度数是∠B 的度数
的3倍,∠C 比∠B 大15°,求∠A,∠B,∠C
的度数.
典例精讲
变式: 已知:如图,AB与CD相交于点E.
求证:∠A+∠C=∠B+∠D.
变式训练
整体思想
一个三角形的三个内角中, 最多有几个直角?
最多有几个钝角?
三角形的内角和等于180°,
因此最多有一个直角
或一个钝角.
七嘴八舌
知识点二:
三角形的分类
三角形按角如何分类呢?
探究
锐角三角形
直角三角形
三角形按角如何分类呢?
探究
三角形中,三个角都是锐角的三角形叫锐角三角形,
有一个角是直角的三角形叫直角三角形,
有一个角是钝角的三角形叫钝角三角形
锐角三角形
钝角三角形
直角三角形
三角形按角大小分类:
三角形
锐角三角形(三个角为锐角)
钝角三角形(一个角为钝角)
直角三角形(一个角为直角)
斜三角形
A
B
C
D
BD是AB的延长线
BC是△ ABC的边
定义:三角形的一边与另一边的延长线
所组成的角叫做三角形的外角.
你能说出∠CBD的边与△ABC的边的关系吗?
三角形的外角
相邻的
内角
不相邻的内角
不相邻的内角
三角形的外角与相邻内角互为_____。
补角
三角形的外角与不相邻的内角有什么关系?
知识点三:
三角形的内角与外角的关系
∠ACD+ ∠ACB =180°
∠A+ ∠B+ ∠ACB =180°
所以, ∠A+ ∠B= ∠ACD
解:
B
C
D
A
∵∠ACD是△ ABC的外角
∴∠ACD= ∠A+ ∠B
三角形的一个外角等于与它不相邻的两个内角的和。
几何语言:
结论:
思考:1、如何说明 ∠ACD= ∠B+ ∠ A?
思考:1、试说明 ∠ACD与 ∠B、 ∠ACD与 ∠ A的大小关系?
D
A
B
三角形的一个外角大于任何
一个不相邻的内角。
推论:
1、n=____ x=_____ y=_____
27
29
59
课堂检测
2、在△ABC中,
(1)已知∠A=80°,∠B=52°, 则∠C=__
(2)已知∠A=80°, ∠B-∠C= 40°,则∠C= __
(3)已知∠A :∠B : ∠C =1:3:5,能否求
∠A 、∠B、∠C的度数?
48°
30°
课堂检测
3、当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为_______.
课堂检测
4、如图,一个60°的角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为( )
A. 120° B. 180° C. 240° D. 300°
5、如图,∠1+∠2+∠3+∠4= ______度.
如图所示:求∠A+∠B+∠C+∠D+∠E的度数?
E
D
C
B
A
1
2
解:∵∠1= ∠A+ ∠D
(三角形的外角等于与它不相邻的两内角的和)
又∵∠2= ∠B+ ∠E
(三角形的外角等于与它不相邻的两内角的和)
∴ ∠A+∠B+∠C+∠D+∠E
=(∠A+ ∠D)+(∠B+ ∠E)+∠C
=∠1+∠2+∠C
=180°
智勇大比拼!
直角三角形可用符号“Rt△” 来表示, 例如直角三角形ABC 可以记作“Rt△ABC”.
在直角三角形中, 夹直角的两边叫作直角边,
直角的对边叫作斜边.
两条直角边相等的直角三角形叫作等腰直角三角形.
同课章节目录
