湘教版(2012)初中数学八年级上册2.3 等腰三角形 课件(共21张ppt)
文档属性
| 名称 | 湘教版(2012)初中数学八年级上册2.3 等腰三角形 课件(共21张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览


文档简介
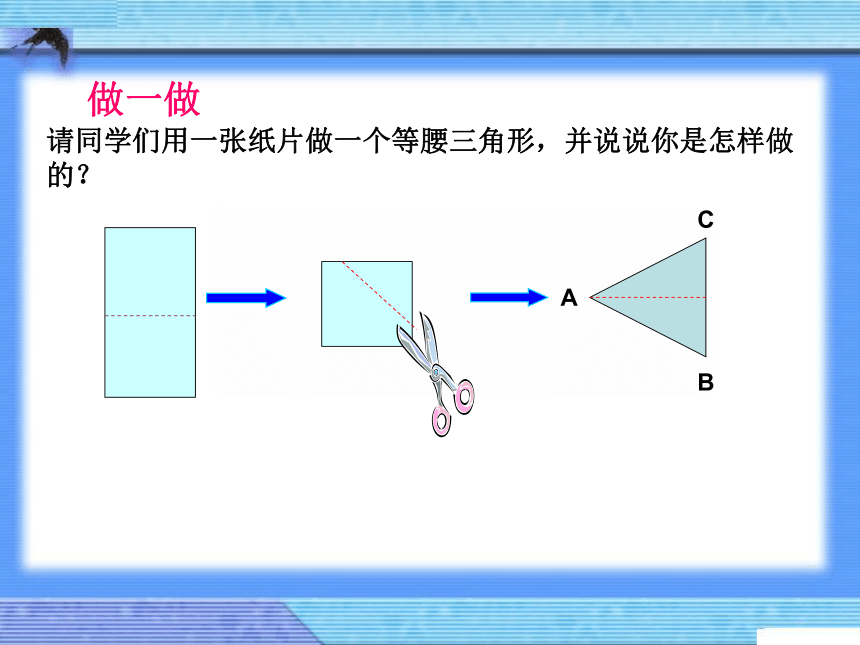
做一做
A
C
B
请同学们用一张纸片做一个等腰三角形,并说说你是怎样做的?
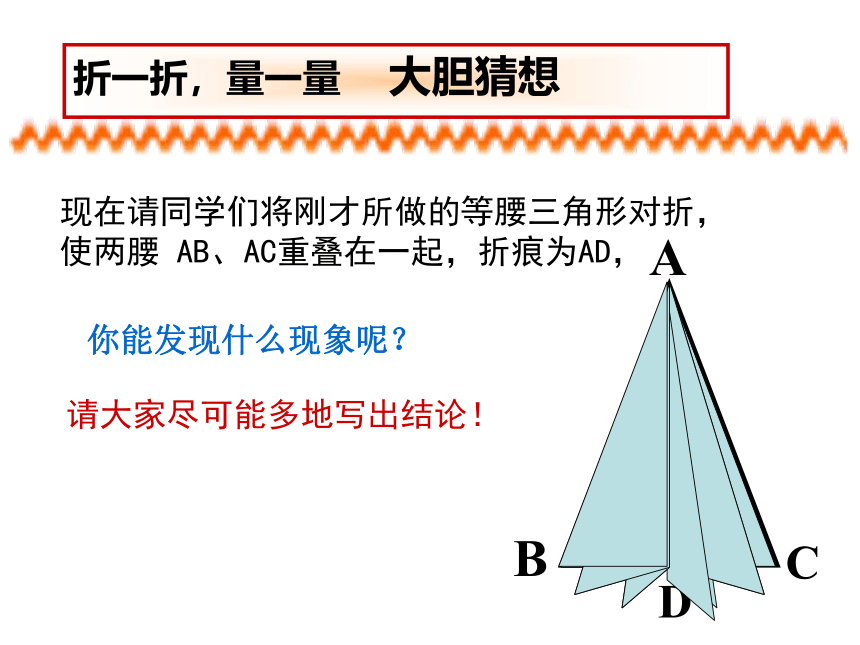
现在请同学们将刚才所做的等腰三角形对折,
使两腰 AB、AC重叠在一起,折痕为AD,
请大家尽可能多地写出结论!
D
A
B
C
折一折,量一量 大胆猜想
你能发现什么现象呢?
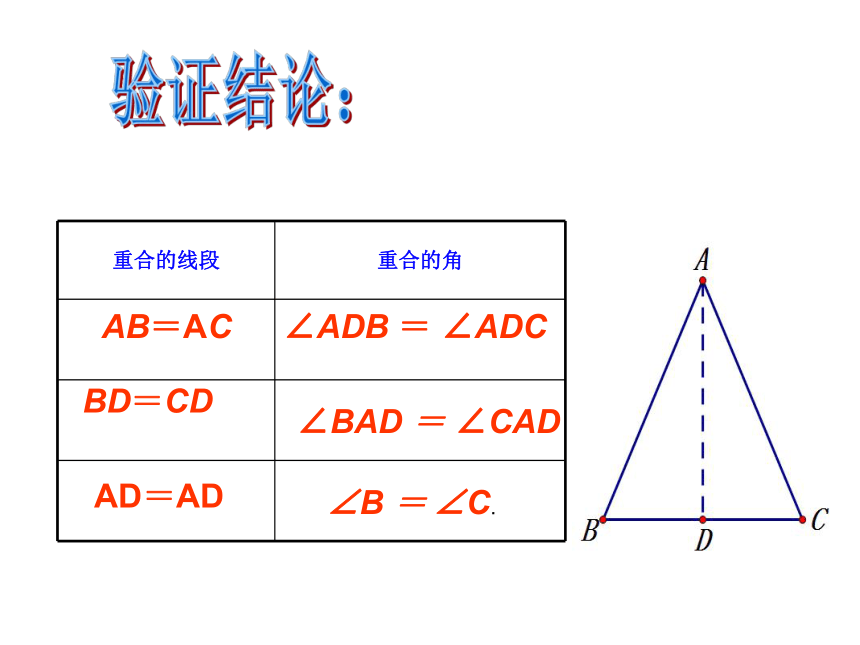
重合的线段
重合的角
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC
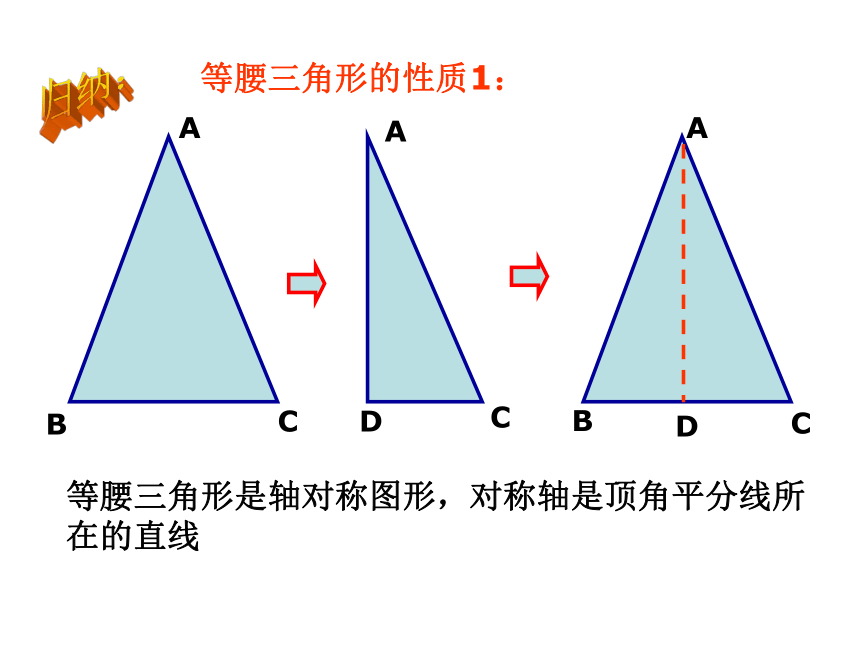
等腰三角形的性质1:
A
B
C
A
D
C
A
B
C
D
等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线
A
B
C
D
A
B
C
D
┓
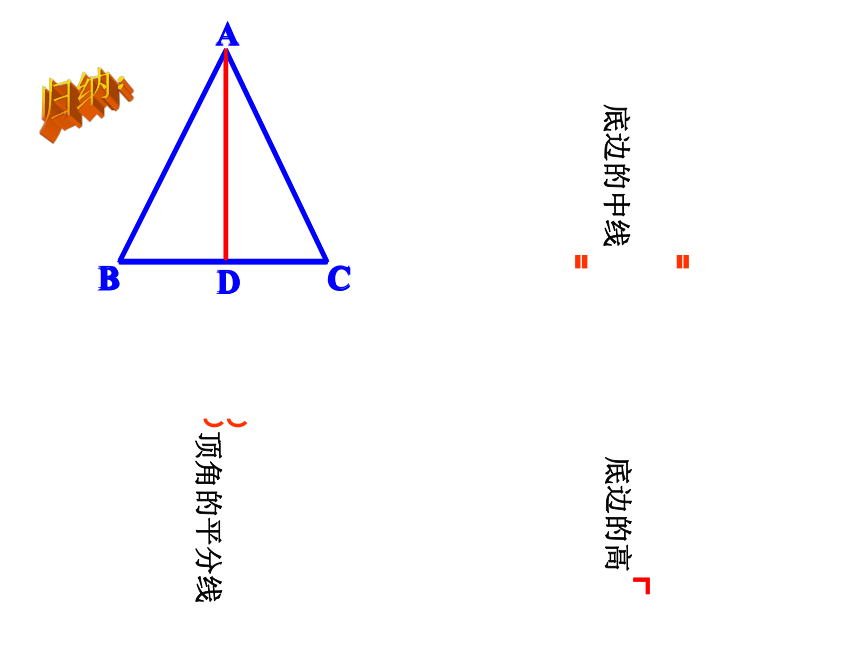
顶角的平分线
底边的高
底边的中线
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
┓
A
B
C
D
A
B
C
D
A
B
C
D
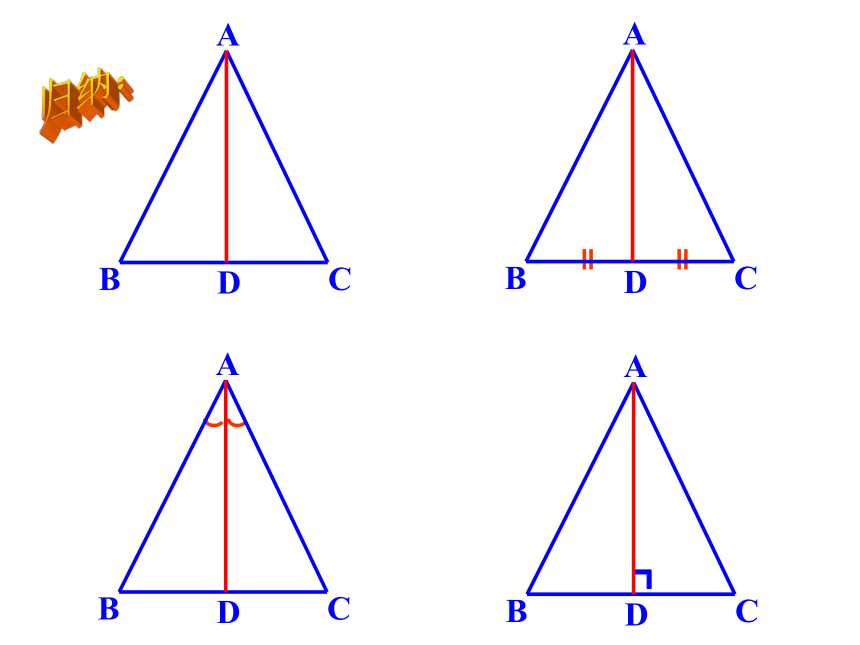
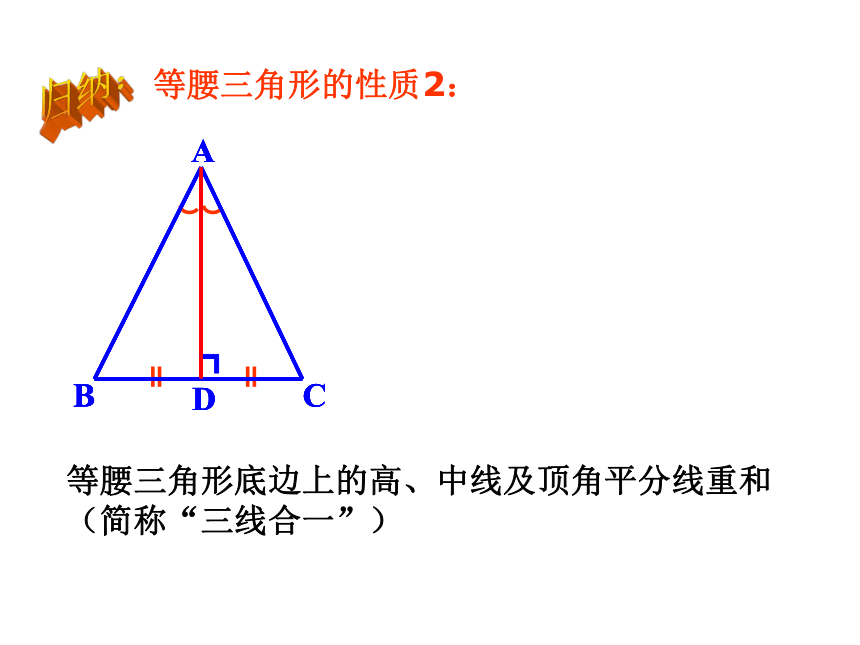
等腰三角形的性质2:
等腰三角形底边上的高、中线及顶角平分线重和
(简称“三线合一”)
A
B
C
D
A
B
C
D
┓
A
B
C
D
C
B
A
等腰三角形的两个底角相等(简写成“等边对等角”)
等腰三角形的性质3:
动脑筋
如图,△ABC是等边三角形,那么∠A,∠B,∠C 的大小之间有什么关系呢?
因为△ABC是等边三角形,
所以AB=AC=BC,
从而∠A=∠B=∠C.
由三角形内角和定理可得:
∠A=∠B=∠C=60°.
由此得到等边三角形的如下性质:
等边三角形的三个内角相等,且都等于60°.
结论
由于等边三角形是特殊的等腰三角形,因此等边三角形也是_______图形,它有______对称轴,分别是三个内角的_______所在的直线.
结论
轴对称
三条
平分线
例1 已知:如图,在△ABC中,AB=AC,点D,E
在边BC上,且AD=AE.
求证:BD=CE.
举
例
证明 作AF⊥BC,垂足为点F,
则AF是等腰三角形ABC和等腰三角形ADE底边上的高,也是底边上的中线.
∴ BF=CF,
∴ BF-DF=CF-EF,
DF=EF,
即 BD=CE.
F
如图的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,调整架身,使点A恰好在铅锤线上.
(1)AD与BC是否垂直,试说明理由.
(2)这时BC处于水平位置,为什么?
议一议
你能说出其中的道理吗?
练习
1. 如图,在△ABC中,AB=AC,AD为BC边上
的高,∠BAC=49°,BC= 4,求∠BAD的度
数及DC的长.
答:∠BAD=24.5°,
DC=2.
做一做
2. 如图,点P为等边三角形ABC的边BC上一
点,且∠APD= 80°,AD=AP,求∠DPC
的度数.
答:∠DPC =20°.
练习
做一做
我知道了… …
我感受了… …
我做了… …
寄语同学
尽管在我们前进的道路上,总会荆棘丛生,坎坷不平,但只要我们把信心、决心、恒心
“三心合一”,我们就一定能迎难而上,奋勇向前。
1.基础作业:教材第66页第1题、第2题
2.探究性作业:等腰三角形两个外角之比是1:4,你能得出它顶角的度数吗?
布置作业
再见
A
C
B
请同学们用一张纸片做一个等腰三角形,并说说你是怎样做的?
现在请同学们将刚才所做的等腰三角形对折,
使两腰 AB、AC重叠在一起,折痕为AD,
请大家尽可能多地写出结论!
D
A
B
C
折一折,量一量 大胆猜想
你能发现什么现象呢?
重合的线段
重合的角
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC
等腰三角形的性质1:
A
B
C
A
D
C
A
B
C
D
等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线
A
B
C
D
A
B
C
D
┓
顶角的平分线
底边的高
底边的中线
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
┓
A
B
C
D
A
B
C
D
A
B
C
D
等腰三角形的性质2:
等腰三角形底边上的高、中线及顶角平分线重和
(简称“三线合一”)
A
B
C
D
A
B
C
D
┓
A
B
C
D
C
B
A
等腰三角形的两个底角相等(简写成“等边对等角”)
等腰三角形的性质3:
动脑筋
如图,△ABC是等边三角形,那么∠A,∠B,∠C 的大小之间有什么关系呢?
因为△ABC是等边三角形,
所以AB=AC=BC,
从而∠A=∠B=∠C.
由三角形内角和定理可得:
∠A=∠B=∠C=60°.
由此得到等边三角形的如下性质:
等边三角形的三个内角相等,且都等于60°.
结论
由于等边三角形是特殊的等腰三角形,因此等边三角形也是_______图形,它有______对称轴,分别是三个内角的_______所在的直线.
结论
轴对称
三条
平分线
例1 已知:如图,在△ABC中,AB=AC,点D,E
在边BC上,且AD=AE.
求证:BD=CE.
举
例
证明 作AF⊥BC,垂足为点F,
则AF是等腰三角形ABC和等腰三角形ADE底边上的高,也是底边上的中线.
∴ BF=CF,
∴ BF-DF=CF-EF,
DF=EF,
即 BD=CE.
F
如图的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,调整架身,使点A恰好在铅锤线上.
(1)AD与BC是否垂直,试说明理由.
(2)这时BC处于水平位置,为什么?
议一议
你能说出其中的道理吗?
练习
1. 如图,在△ABC中,AB=AC,AD为BC边上
的高,∠BAC=49°,BC= 4,求∠BAD的度
数及DC的长.
答:∠BAD=24.5°,
DC=2.
做一做
2. 如图,点P为等边三角形ABC的边BC上一
点,且∠APD= 80°,AD=AP,求∠DPC
的度数.
答:∠DPC =20°.
练习
做一做
我知道了… …
我感受了… …
我做了… …
寄语同学
尽管在我们前进的道路上,总会荆棘丛生,坎坷不平,但只要我们把信心、决心、恒心
“三心合一”,我们就一定能迎难而上,奋勇向前。
1.基础作业:教材第66页第1题、第2题
2.探究性作业:等腰三角形两个外角之比是1:4,你能得出它顶角的度数吗?
布置作业
再见
同课章节目录
