湘教版(2012)初中数学八年级上册2.3 等腰三角形 课件(共32张ppt)
文档属性
| 名称 | 湘教版(2012)初中数学八年级上册2.3 等腰三角形 课件(共32张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览







文档简介
等腰三角形
本课内容
本节内容
2.3
我们前面已经学习了三角形的一些性质,那么等腰三角形除了具有一般三角形的性质外,还具有哪些特殊的性质呢?
探究
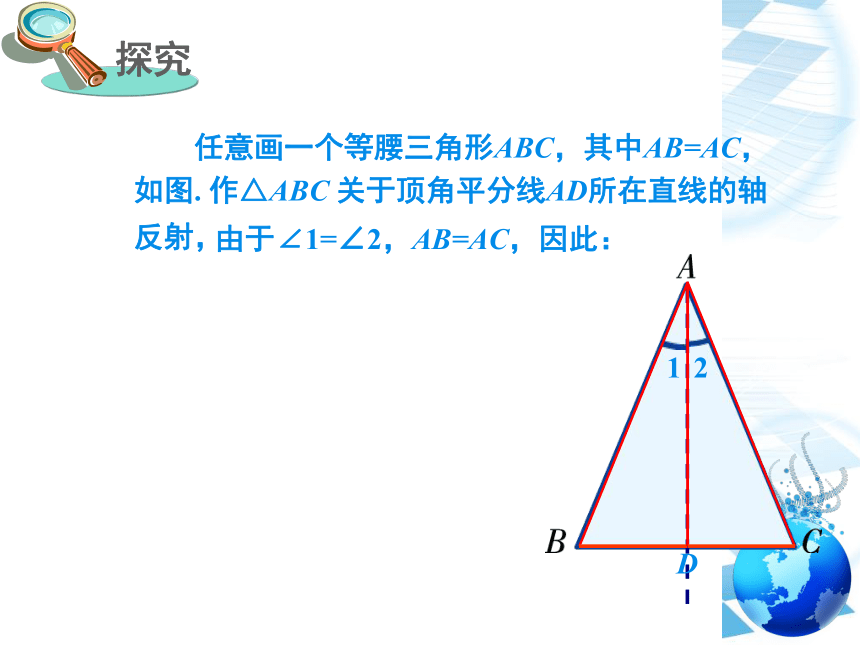
任意画一个等腰三角形ABC,其中AB=AC,如图.
作△ABC 关于顶角平分线AD所在直线的轴反射,
由于∠1=∠2,AB=AC,因此:
D
1
2
射线AB的像是射线AC,
射线AC的像是射线 ;
线段AB的像是线段AC,
线段AC的像是线段 ;
点B的像是点C,
点C的像是点 ;
线段BC的像是线段CB.
从而等腰三角形ABC关于直线 对称.
AB
AB
B
AD
由于点D的像是点D,
因此线段DB的像是线段 ,
从而AD是底边BC上的 .
由于射线DB的像是射线DC,
射线DA的像是射线 ,
因此∠BDA ∠CDA= °,
从而AD是底边BC上的 .
由于射线BA的像是射线CA,
射线BC的像是射线 ,
因此∠B ∠C.
DC
中线
DA
=
90
高
CB
=
结论
由此得到等腰三角形的性质定理:
等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线.
等腰三角形的两底角相等( 简称“等边对等角”).
结论
等腰三角形底边上的高、中线及顶角平分线重合(简称为“三线合一”).
动脑筋
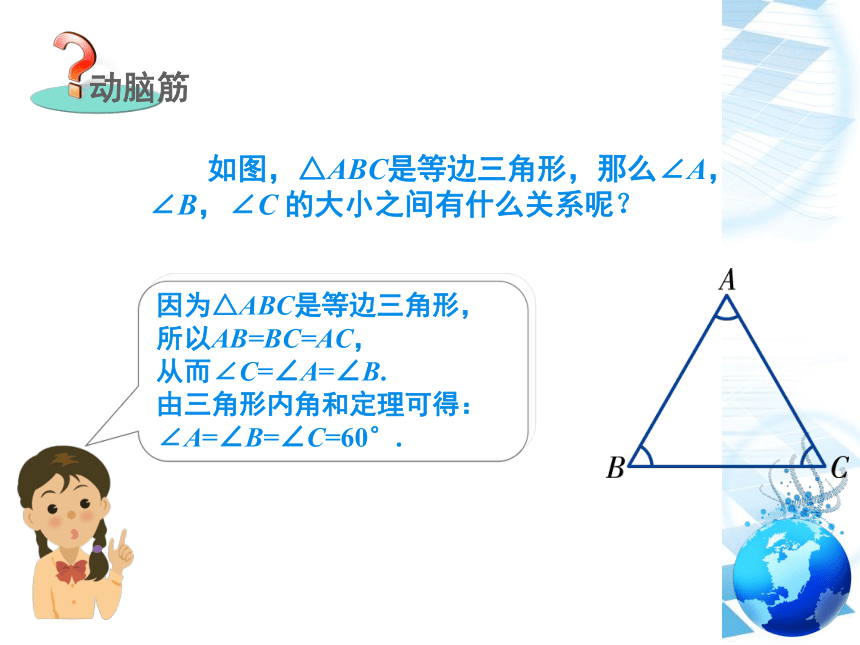
因为△ABC是等边三角形,
所以AB=BC=AC,
从而∠C=∠A=∠B.
由三角形内角和定理可得:
∠A=∠B=∠C=60°.
如图,△ABC是等边三角形,那么∠A,∠B,∠C 的大小之间有什么关系呢?
由此得到等边三角形的如下性质:
等边三角形的三个内角相等,且都等于60°.
结论
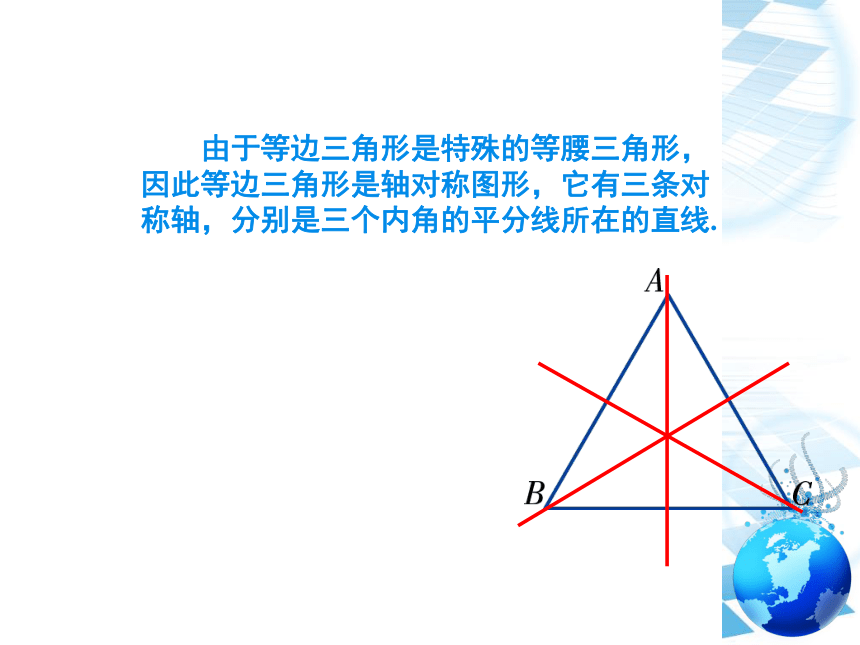
由于等边三角形是特殊的等腰三角形,因此等边三角形是轴对称图形,它有三条对称轴,分别是三个内角的平分线所在的直线.
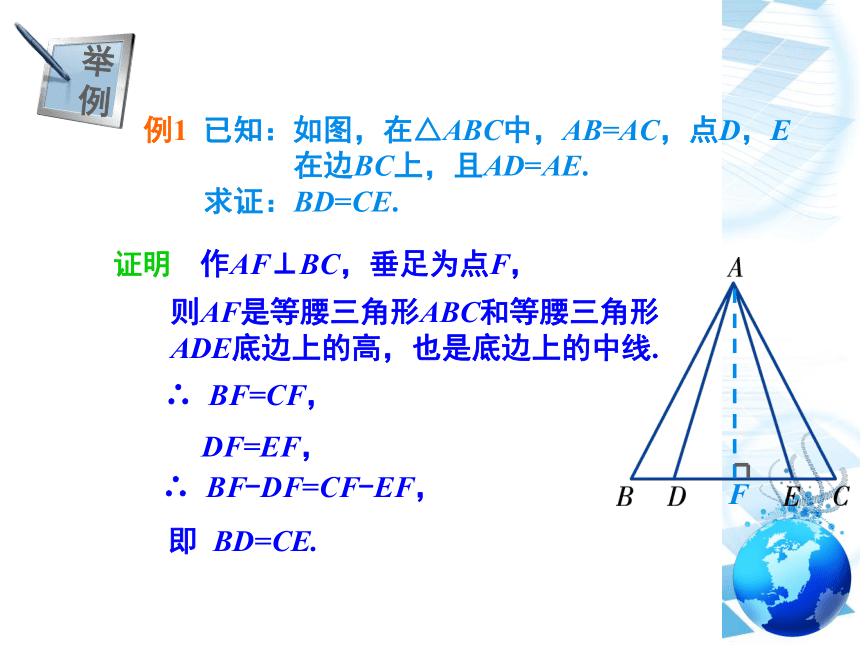
例1 已知:如图,在△ABC中,AB=AC,点D,E
在边BC上,且AD=AE.
求证:BD=CE.
举
例
证明 作AF⊥BC,垂足为点F,
则AF是等腰三角形ABC和等腰三角形ADE底边上的高,也是底边上的中线.
∴ BF=CF,
∴ BF-DF=CF-EF,
DF=EF,
即 BD=CE.
F
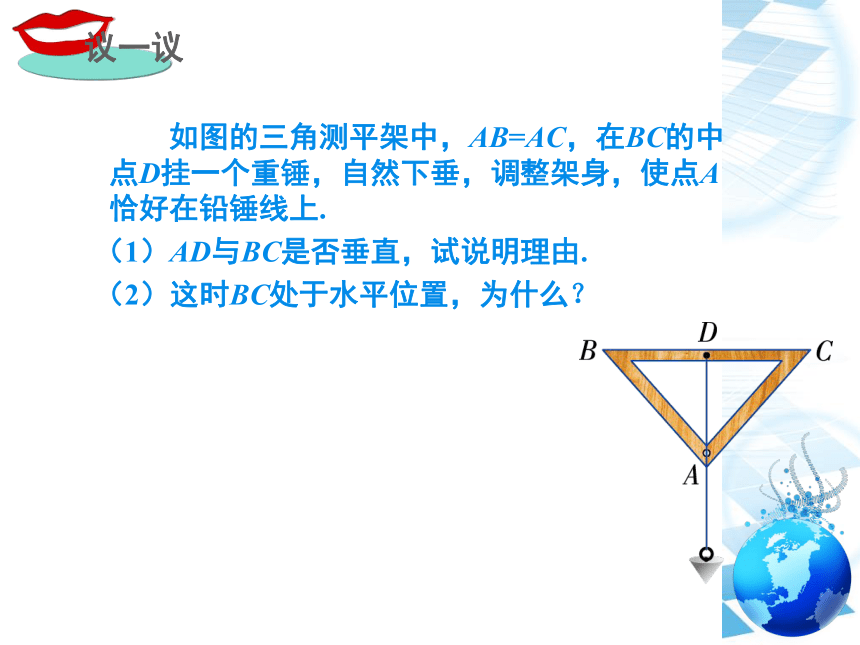
如图的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,调整架身,使点A恰好在铅锤线上.
(1)AD与BC是否垂直,试说明理由.
(2)这时BC处于水平位置,为什么?
议一议
练习
1. 如图,在△ABC中,AB=AC,AD为BC边上
的高,∠BAC=49°,BC= 4,求∠BAD的度
数及DC的长.
答:∠BAD=24.5°,
DC=2.
2. 如图,点P为等边三角形ABC的边BC上一
点,且∠APD= 80°,AD=AP,求∠DPC
的度数.
答:∠DPC =20°.
我们知道,等腰三角形的两底角相等,反过来,两个角相等的三角形是等腰三角形吗?
探究
如图,在△ABC中,如果∠B=∠C,那么AB与AC之间有什么关系吗?
我测量后发现AB与AC相等.
3cm
3cm
事实上,如图,在△ABC中,∠B=∠C.
沿过点A的直线把∠BAC对折,
得∠BAC的平分线AD交BC于点D,
则∠1=∠2.
又∠B=∠C,
由三角形内角和的性质得
∠ADB=∠ADC.
D
1
2
沿AD所在直线折叠,
由于∠ADB=∠ADC,∠1=∠2,
所以射线DB与射线DC重合,
射线AB与射线AC重合.
从而点B与点C重合,
于是AB=AC.
结论
有两个角相等的三角形是等腰三角形(简称“等角对等边”).
结论
三个角都是60°的三角形是等边三角形.
由此并且结合三角形内角和定理,还可以得到等边三角形的判定定理:
例2 已知:如图,在△ABC中,AB=AC,点D,E
分别是AB,AC上的点,且DE∥BC.
求证:△ADE为等腰三角形.
举
例
证明 ∵AB=AC,
∴ ∠B=∠C.
又∵ DE∥BC,
∴ ∠ADE=∠B,∠AED=∠C.
∴ ∠ADE=∠AED.
于是△ADE为等腰三角形.
有一个角是60°的等腰三角形是等边三角形吗?为什么?
动脑筋
如图,在等腰三角形ABC中,
AB=AC.
由三角形内角和定理得
∠A+∠B+∠C= 180°.
如果顶角∠A=60°,
则∠B+∠C= 180°-60°=120°.
又 AB=AC,
∴ ∠B=∠C.
∴ ∠B=∠C=∠A=60°.
∴ △ABC是等边三角形.
由此得到另一条等边三角形的判定定理:
结论
有一个角是60°的等腰三角形是等边三角形
例3 已知:如图,△ABC是等边三角形,点D,E
分别在BA,CA的延长线上,且AD=AE.
求证:△ADE是等边三角形.
举
例
证明 ∵△ABC是等边三角形,
∴∠BAC=∠B=∠C= 60°.
∵∠EAD=∠BAC= 60°,
又 AD =AE,
∴△ADE是等边三角形
(有一个角是60°的等腰三角形是等边三角形)
练习
1. 已知:等腰三角形ABC的底角∠ABC和
∠ACB的平分线相交于点O.
求证:△OBC为等腰三角形.
A
B
C
D
E
O
证明
∵∠ABC和∠ACB的平分线相交于点O,
∴ ∠ABD =∠DBC= ,
∠ACE =∠ECB= ,
∴ ∠DBC =∠ECB,
∴ △OBC是等腰三角形.
又∵ △ABC是等腰三角形,
∴ ∠ABC =∠ACB,
A
B
C
D
E
O
2. 已知:如图,CD平分∠ACB,AE∥DC,AE
交BC的延长线于点E,且∠ACE= 60°.
求证:△ACE是等边三角形.
证明
∵CD平分∠ACB,
∴ 在△ACE中,∠CAE= 180°- ∠E -∠ACE =60 °
又∵∠ACE=60°,
∴ ∠BCD=∠E=60°,
∴ ∠ACD =∠DCB,
∴ ∠ACD=∠DCB=60°,
又 ∵ AE∥DC,
∴ ∠CAE = ∠ACE=∠E=60°
∴△ACE是等边三角形.
3. 已知:如图,AB=BC ,∠CDE= 120°,
DF∥BA,且DF平分∠CDE.
求证:△ABC是等边三角形.
证明
∵ AB=BC,
∴△ABC是等边三角形.
又∵∠CDE=120°,DF平分∠CDE.
∴ ∠FDC=∠ABC=60°,
∴ △ABC是等腰三角形,
∴ ∠EDF=∠FDC=60°,
又∵DF∥BA,
中考 试题
例1
等腰三角形两边长分别是2cm和5cm,则这个三角形周长为( )
A.9cm B.12cm
C.9cm或12cm D.14cm
B
解析
另一边长为2cm或5cm,2,2,5不符合三角形三边关系定理,故选5.
∴周长为5+5+2=12cm.
中考 试题
例2
若等腰三角形中有一个角等于50°,则这个等腰三角形的顶角的度数为( )
A. 50° B. 80°
C. 65°或50° D. 50°或80°
解析
因为50°可作为等腰三角形的一顶角或一底角,故选D.
D
结 束
本课内容
本节内容
2.3
我们前面已经学习了三角形的一些性质,那么等腰三角形除了具有一般三角形的性质外,还具有哪些特殊的性质呢?
探究
任意画一个等腰三角形ABC,其中AB=AC,如图.
作△ABC 关于顶角平分线AD所在直线的轴反射,
由于∠1=∠2,AB=AC,因此:
D
1
2
射线AB的像是射线AC,
射线AC的像是射线 ;
线段AB的像是线段AC,
线段AC的像是线段 ;
点B的像是点C,
点C的像是点 ;
线段BC的像是线段CB.
从而等腰三角形ABC关于直线 对称.
AB
AB
B
AD
由于点D的像是点D,
因此线段DB的像是线段 ,
从而AD是底边BC上的 .
由于射线DB的像是射线DC,
射线DA的像是射线 ,
因此∠BDA ∠CDA= °,
从而AD是底边BC上的 .
由于射线BA的像是射线CA,
射线BC的像是射线 ,
因此∠B ∠C.
DC
中线
DA
=
90
高
CB
=
结论
由此得到等腰三角形的性质定理:
等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线.
等腰三角形的两底角相等( 简称“等边对等角”).
结论
等腰三角形底边上的高、中线及顶角平分线重合(简称为“三线合一”).
动脑筋
因为△ABC是等边三角形,
所以AB=BC=AC,
从而∠C=∠A=∠B.
由三角形内角和定理可得:
∠A=∠B=∠C=60°.
如图,△ABC是等边三角形,那么∠A,∠B,∠C 的大小之间有什么关系呢?
由此得到等边三角形的如下性质:
等边三角形的三个内角相等,且都等于60°.
结论
由于等边三角形是特殊的等腰三角形,因此等边三角形是轴对称图形,它有三条对称轴,分别是三个内角的平分线所在的直线.
例1 已知:如图,在△ABC中,AB=AC,点D,E
在边BC上,且AD=AE.
求证:BD=CE.
举
例
证明 作AF⊥BC,垂足为点F,
则AF是等腰三角形ABC和等腰三角形ADE底边上的高,也是底边上的中线.
∴ BF=CF,
∴ BF-DF=CF-EF,
DF=EF,
即 BD=CE.
F
如图的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,调整架身,使点A恰好在铅锤线上.
(1)AD与BC是否垂直,试说明理由.
(2)这时BC处于水平位置,为什么?
议一议
练习
1. 如图,在△ABC中,AB=AC,AD为BC边上
的高,∠BAC=49°,BC= 4,求∠BAD的度
数及DC的长.
答:∠BAD=24.5°,
DC=2.
2. 如图,点P为等边三角形ABC的边BC上一
点,且∠APD= 80°,AD=AP,求∠DPC
的度数.
答:∠DPC =20°.
我们知道,等腰三角形的两底角相等,反过来,两个角相等的三角形是等腰三角形吗?
探究
如图,在△ABC中,如果∠B=∠C,那么AB与AC之间有什么关系吗?
我测量后发现AB与AC相等.
3cm
3cm
事实上,如图,在△ABC中,∠B=∠C.
沿过点A的直线把∠BAC对折,
得∠BAC的平分线AD交BC于点D,
则∠1=∠2.
又∠B=∠C,
由三角形内角和的性质得
∠ADB=∠ADC.
D
1
2
沿AD所在直线折叠,
由于∠ADB=∠ADC,∠1=∠2,
所以射线DB与射线DC重合,
射线AB与射线AC重合.
从而点B与点C重合,
于是AB=AC.
结论
有两个角相等的三角形是等腰三角形(简称“等角对等边”).
结论
三个角都是60°的三角形是等边三角形.
由此并且结合三角形内角和定理,还可以得到等边三角形的判定定理:
例2 已知:如图,在△ABC中,AB=AC,点D,E
分别是AB,AC上的点,且DE∥BC.
求证:△ADE为等腰三角形.
举
例
证明 ∵AB=AC,
∴ ∠B=∠C.
又∵ DE∥BC,
∴ ∠ADE=∠B,∠AED=∠C.
∴ ∠ADE=∠AED.
于是△ADE为等腰三角形.
有一个角是60°的等腰三角形是等边三角形吗?为什么?
动脑筋
如图,在等腰三角形ABC中,
AB=AC.
由三角形内角和定理得
∠A+∠B+∠C= 180°.
如果顶角∠A=60°,
则∠B+∠C= 180°-60°=120°.
又 AB=AC,
∴ ∠B=∠C.
∴ ∠B=∠C=∠A=60°.
∴ △ABC是等边三角形.
由此得到另一条等边三角形的判定定理:
结论
有一个角是60°的等腰三角形是等边三角形
例3 已知:如图,△ABC是等边三角形,点D,E
分别在BA,CA的延长线上,且AD=AE.
求证:△ADE是等边三角形.
举
例
证明 ∵△ABC是等边三角形,
∴∠BAC=∠B=∠C= 60°.
∵∠EAD=∠BAC= 60°,
又 AD =AE,
∴△ADE是等边三角形
(有一个角是60°的等腰三角形是等边三角形)
练习
1. 已知:等腰三角形ABC的底角∠ABC和
∠ACB的平分线相交于点O.
求证:△OBC为等腰三角形.
A
B
C
D
E
O
证明
∵∠ABC和∠ACB的平分线相交于点O,
∴ ∠ABD =∠DBC= ,
∠ACE =∠ECB= ,
∴ ∠DBC =∠ECB,
∴ △OBC是等腰三角形.
又∵ △ABC是等腰三角形,
∴ ∠ABC =∠ACB,
A
B
C
D
E
O
2. 已知:如图,CD平分∠ACB,AE∥DC,AE
交BC的延长线于点E,且∠ACE= 60°.
求证:△ACE是等边三角形.
证明
∵CD平分∠ACB,
∴ 在△ACE中,∠CAE= 180°- ∠E -∠ACE =60 °
又∵∠ACE=60°,
∴ ∠BCD=∠E=60°,
∴ ∠ACD =∠DCB,
∴ ∠ACD=∠DCB=60°,
又 ∵ AE∥DC,
∴ ∠CAE = ∠ACE=∠E=60°
∴△ACE是等边三角形.
3. 已知:如图,AB=BC ,∠CDE= 120°,
DF∥BA,且DF平分∠CDE.
求证:△ABC是等边三角形.
证明
∵ AB=BC,
∴△ABC是等边三角形.
又∵∠CDE=120°,DF平分∠CDE.
∴ ∠FDC=∠ABC=60°,
∴ △ABC是等腰三角形,
∴ ∠EDF=∠FDC=60°,
又∵DF∥BA,
中考 试题
例1
等腰三角形两边长分别是2cm和5cm,则这个三角形周长为( )
A.9cm B.12cm
C.9cm或12cm D.14cm
B
解析
另一边长为2cm或5cm,2,2,5不符合三角形三边关系定理,故选5.
∴周长为5+5+2=12cm.
中考 试题
例2
若等腰三角形中有一个角等于50°,则这个等腰三角形的顶角的度数为( )
A. 50° B. 80°
C. 65°或50° D. 50°或80°
解析
因为50°可作为等腰三角形的一顶角或一底角,故选D.
D
结 束
同课章节目录
