湘教版(2012)初中数学八年级上册2.3 等腰三角形课件(共16张ppt)
文档属性
| 名称 | 湘教版(2012)初中数学八年级上册2.3 等腰三角形课件(共16张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1002.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览





文档简介
2.3 等腰三角形(1)
A
B
C
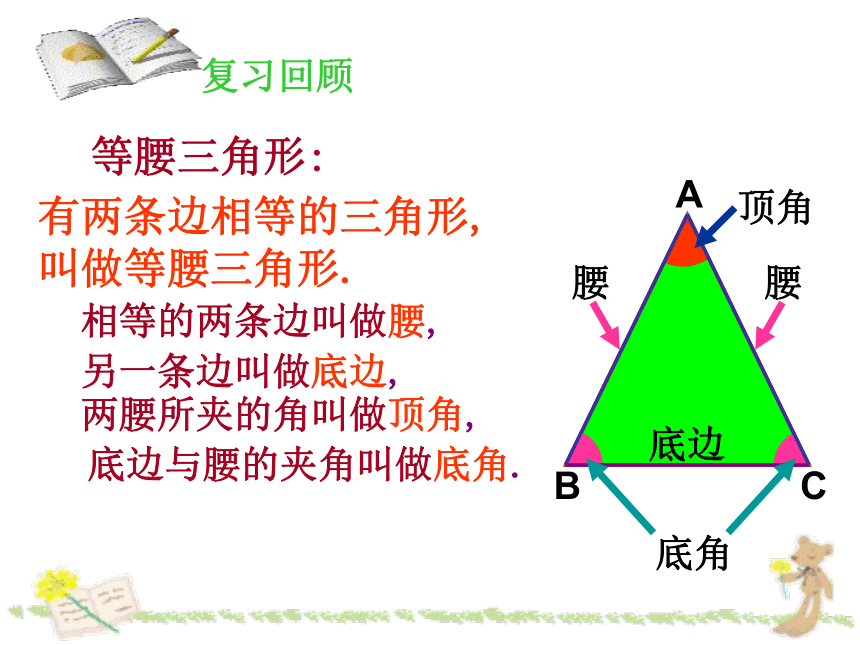
等腰三角形:
有两条边相等的三角形,
叫做等腰三角形.
相等的两条边叫做腰,
另一条边叫做底边,
底边与腰的夹角叫做底角.
两腰所夹的角叫做顶角,
腰
腰
底边
顶角
底角
复习回顾
将手中的等腰三角形对折之后,找出其中重合的线段和角.
等腰三角形是轴对称图形吗?
探究
任意的给你一个等腰三角形ABC,AB=AC,请你将手中的等腰三角形对折,使得AB与AC重合。
重合的线段
重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC
通过表格中的信息,你能够归纳出等腰三角形有哪些性质呢?
归纳总结
等腰三角形的两底角相等( 简称“等边对等角”).
结论
等腰三角形底边上的高、中线及顶角平分线重合(简称为“三线合一”).
等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线.
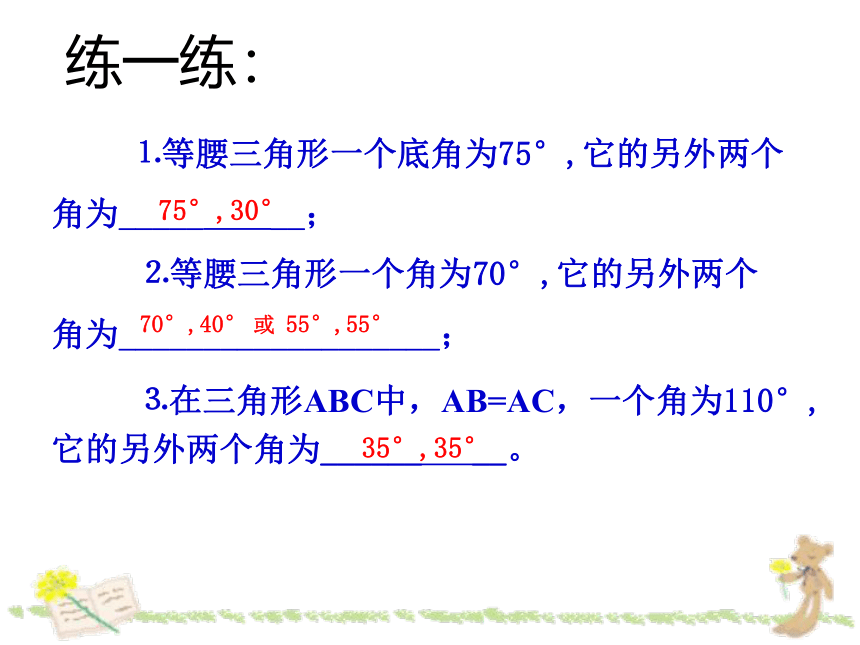
练一练:
⒈等腰三角形一个底角为75°,它的另外两个
角为_____ __;
⒉等腰三角形一个角为70°,它的另外两个
角为___________________;
⒊在三角形ABC中,AB=AC,一个角为110°,它的另外两个角为______ __。
75°,30°
70°,40°
或 55°,55°
35°,35°
1、等腰三角形的顶角一定是锐角。
2、等腰三角形的底角可能是锐角或者直角、
钝角都可以。
3、等腰三角形的顶角平分线一定垂直底边。
4、等腰三角形的角平分线、中线和高互相重
合。
5、等腰三角形底边上的中线一定平分顶角
(X)
(X)
(√)
(X)
(√)
在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,
____=____;
(2)∵AB=AC,AD是中线,
∴∠_ =∠_ ,
____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,
____=____。
A
B
C
D
符号语言:
BAD
CAD
BD
CD
BAD
CAD
AD
BC
AD
BC
BD
CD
如图,点D,E在△ABC中的BC上,AB=AC,
AD=AE,求证:BD=CE(提示:作辅助线)
A
B
C
D
E
作AF⊥BC,垂足为点F。
∵AB=AC,AD=AE,
∴BF=CF,DF=EF,
∴BF-DF=CF-EF,
即 BD=CE.
┐
F
典例欣赏
证明
学以致用
如图,在△ABC中,AB=AC,AD为BC边上的高,∠BAC=49°,BC= 4,求∠BAD的度数及DC的长.
解:
(等腰三角形“三线合一”)
动脑筋
因为△ABC是等边三角形,
所以AB=BC=AC,
从而∠C=∠A=∠B.
由三角形内角和定理可得:
∠A=∠B=∠C=60°.
如图,△ABC是等边三角形,那么∠A,∠B,∠C 的大小之间有什么关系呢?
由于等边三角形是特殊的等腰三角形,因此等边三角形是轴对称图形,它有三条对称轴,分别是三个内角的平分线所在的直线.
由此得到等边三角形的性质:
等边三角形的三个内角相等,且都等于60°
结论
1、如图,点P为等边三角形ABC的边BC上一 点,且∠APD= 80°,AD=AP,求∠DPC的度数.
解:
练习
议一议:
如图中的三角测平架中,AB=AC,在BC的中
点D挂一个重锤,自然下垂,调整架身,使点
A恰好在铅垂线上。
(1)AD与BC是否垂直,为什么?
(2)这时BC处于水平位置,为什么?
B
D
C
A
通过本节课的学习,你有哪些收获?
课堂小结
试一试
45°, 90°
2. 已知等腰三角形的一个角等于36°,那么它的
另外两个角的度数分别
是 ;
1.等腰三角形一个底角为45°,它的另外两个角为_______
36°, 108°或72°, 72°
4.如图,CE交AB于E,且
CE=CB,∠A=∠B。
求证:CE∥DA。
E
D
C
B
A
3. 如图,在△ABC中,AB=
AC,AD平分∠BAC交BC于
点D,AD=5,CD=2,
求△ABC的面积。
D
C
B
A
A
B
C
等腰三角形:
有两条边相等的三角形,
叫做等腰三角形.
相等的两条边叫做腰,
另一条边叫做底边,
底边与腰的夹角叫做底角.
两腰所夹的角叫做顶角,
腰
腰
底边
顶角
底角
复习回顾
将手中的等腰三角形对折之后,找出其中重合的线段和角.
等腰三角形是轴对称图形吗?
探究
任意的给你一个等腰三角形ABC,AB=AC,请你将手中的等腰三角形对折,使得AB与AC重合。
重合的线段
重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC
通过表格中的信息,你能够归纳出等腰三角形有哪些性质呢?
归纳总结
等腰三角形的两底角相等( 简称“等边对等角”).
结论
等腰三角形底边上的高、中线及顶角平分线重合(简称为“三线合一”).
等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线.
练一练:
⒈等腰三角形一个底角为75°,它的另外两个
角为_____ __;
⒉等腰三角形一个角为70°,它的另外两个
角为___________________;
⒊在三角形ABC中,AB=AC,一个角为110°,它的另外两个角为______ __。
75°,30°
70°,40°
或 55°,55°
35°,35°
1、等腰三角形的顶角一定是锐角。
2、等腰三角形的底角可能是锐角或者直角、
钝角都可以。
3、等腰三角形的顶角平分线一定垂直底边。
4、等腰三角形的角平分线、中线和高互相重
合。
5、等腰三角形底边上的中线一定平分顶角
(X)
(X)
(√)
(X)
(√)
在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,
____=____;
(2)∵AB=AC,AD是中线,
∴∠_ =∠_ ,
____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,
____=____。
A
B
C
D
符号语言:
BAD
CAD
BD
CD
BAD
CAD
AD
BC
AD
BC
BD
CD
如图,点D,E在△ABC中的BC上,AB=AC,
AD=AE,求证:BD=CE(提示:作辅助线)
A
B
C
D
E
作AF⊥BC,垂足为点F。
∵AB=AC,AD=AE,
∴BF=CF,DF=EF,
∴BF-DF=CF-EF,
即 BD=CE.
┐
F
典例欣赏
证明
学以致用
如图,在△ABC中,AB=AC,AD为BC边上的高,∠BAC=49°,BC= 4,求∠BAD的度数及DC的长.
解:
(等腰三角形“三线合一”)
动脑筋
因为△ABC是等边三角形,
所以AB=BC=AC,
从而∠C=∠A=∠B.
由三角形内角和定理可得:
∠A=∠B=∠C=60°.
如图,△ABC是等边三角形,那么∠A,∠B,∠C 的大小之间有什么关系呢?
由于等边三角形是特殊的等腰三角形,因此等边三角形是轴对称图形,它有三条对称轴,分别是三个内角的平分线所在的直线.
由此得到等边三角形的性质:
等边三角形的三个内角相等,且都等于60°
结论
1、如图,点P为等边三角形ABC的边BC上一 点,且∠APD= 80°,AD=AP,求∠DPC的度数.
解:
练习
议一议:
如图中的三角测平架中,AB=AC,在BC的中
点D挂一个重锤,自然下垂,调整架身,使点
A恰好在铅垂线上。
(1)AD与BC是否垂直,为什么?
(2)这时BC处于水平位置,为什么?
B
D
C
A
通过本节课的学习,你有哪些收获?
课堂小结
试一试
45°, 90°
2. 已知等腰三角形的一个角等于36°,那么它的
另外两个角的度数分别
是 ;
1.等腰三角形一个底角为45°,它的另外两个角为_______
36°, 108°或72°, 72°
4.如图,CE交AB于E,且
CE=CB,∠A=∠B。
求证:CE∥DA。
E
D
C
B
A
3. 如图,在△ABC中,AB=
AC,AD平分∠BAC交BC于
点D,AD=5,CD=2,
求△ABC的面积。
D
C
B
A
同课章节目录
