湘教版(2012)初中数学八年级上册2.3 等腰三角形的性质 等腰三角形的性质 课件(共19张ppt)
文档属性
| 名称 | 湘教版(2012)初中数学八年级上册2.3 等腰三角形的性质 等腰三角形的性质 课件(共19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 06:52:44 | ||
图片预览





文档简介
2.3 等腰三角形
第2章 三角形
等腰三角形的性质
学习目标
导入新课
情境引入
建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道为什么吗?
思考
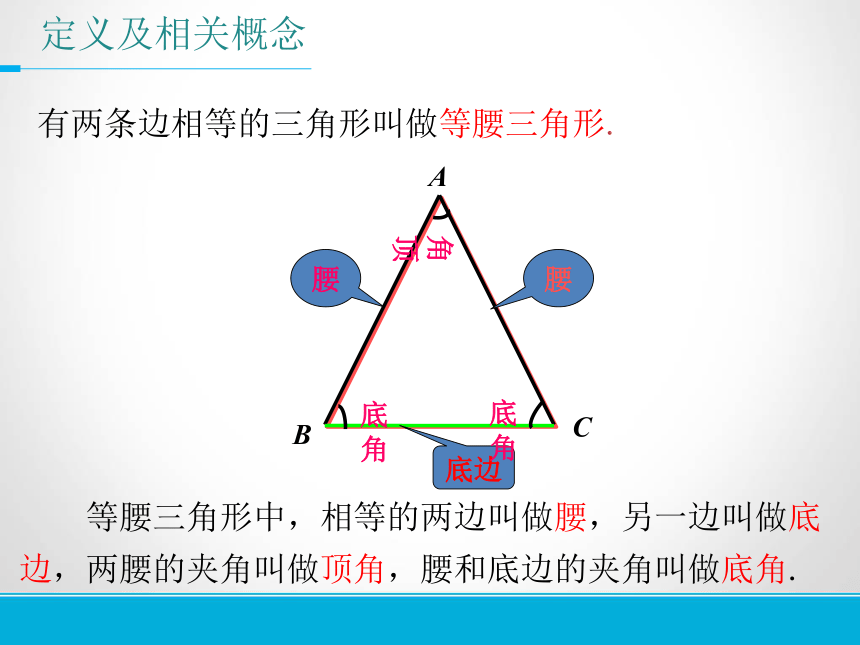
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
角顶
底角
底角
定义及相关概念
讲授新课
等腰三角形的性质
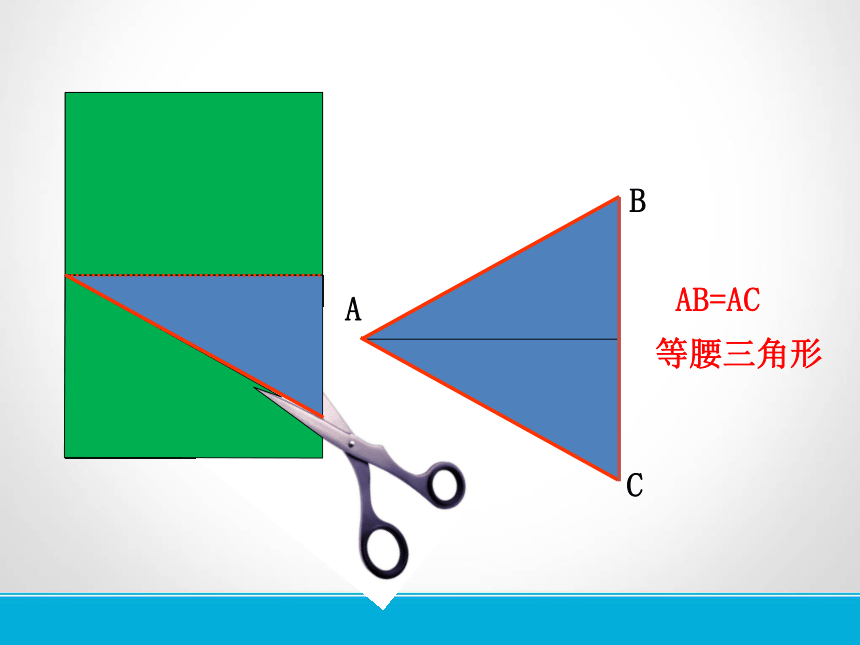
剪一剪:把一张长方形的纸按图中的红线对折,并剪去阴影部分(一个直角三角形),再把得到的直角三角形展开,得到的三角形ABC有什么特点?
互动探究
A
B
C
AB=AC
等腰三角形
折一折:△ABC 是轴对称图形吗?它的对称轴是什么?
A
C
D
B
折痕所在的直线是它的对称轴.
找一找:把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
重合的线段
重合的角
A
C
B
D
AB与AC
BD与CD
AD与AD
∠B 与∠C.
∠BAD 与∠CAD
∠ADB 与∠ADC
等腰三角形是轴对称图形.
猜一猜: 由这些重合的线段和角,你能发现等腰三角形的性质吗?
由此得到等腰三角形的性质定理:
等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线.
等腰三角形的两底角相等(“等边对等角”).
总结归纳
等腰三角形底边上的高、中线及顶角平分线重合(简称为“三线合一”).
填一填:根据等腰三角形性质定理完成下列填空.
在△ABC中, AB=AC时,
(1)∵AD ⊥ BC,
∴∠_____ = ∠_____,____= ____.
(2) ∵AD是中线,
∴____⊥____ ,∠_____=∠_____.
(3) ∵AD是角平分线,
∴____ ⊥____ ,_____=_____.
A
B
C
D
(
(
1
2
1
2
BD
CD
AD
BC
1
2
AD
BC
BD
CD
画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高,看看它们是否重合?
“三线合一”的操作
思考:建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道为什么吗?
等腰三角形一个角为75°,它的另外两个角为
____ __;
牛刀小试
75°, 30°
52.5°, 52.5°
已知:如图,在△ABC中,AB=AC,点D,E在边BC 上,且AD=AE.求证:BD=CE.
F
证明 : 作AF⊥BC,垂足为点F,
则AF是等腰△ABC和等腰△ADE底边上的高,也是底边上的中线.
∴ BF=CF,
DF=EF,
∴ BF-DF=CF-EF,
即 BD=CE.
方法总结:在等腰三角形有关计算或证明中,会遇到一些添加辅助线的问题,其顶角平分线、底边上的高、底边上的中线是常见的辅助线.
勇攀高峰
课堂小结
等腰三角形的性质
等边对等角
三线合一
注意是指同一个三角形中
注意是指顶角的平分线,底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.
课后作业
如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=30°.求∠ADC和∠CAD的度数.
谢 谢!
第2章 三角形
等腰三角形的性质
学习目标
导入新课
情境引入
建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道为什么吗?
思考
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
角顶
底角
底角
定义及相关概念
讲授新课
等腰三角形的性质
剪一剪:把一张长方形的纸按图中的红线对折,并剪去阴影部分(一个直角三角形),再把得到的直角三角形展开,得到的三角形ABC有什么特点?
互动探究
A
B
C
AB=AC
等腰三角形
折一折:△ABC 是轴对称图形吗?它的对称轴是什么?
A
C
D
B
折痕所在的直线是它的对称轴.
找一找:把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
重合的线段
重合的角
A
C
B
D
AB与AC
BD与CD
AD与AD
∠B 与∠C.
∠BAD 与∠CAD
∠ADB 与∠ADC
等腰三角形是轴对称图形.
猜一猜: 由这些重合的线段和角,你能发现等腰三角形的性质吗?
由此得到等腰三角形的性质定理:
等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线.
等腰三角形的两底角相等(“等边对等角”).
总结归纳
等腰三角形底边上的高、中线及顶角平分线重合(简称为“三线合一”).
填一填:根据等腰三角形性质定理完成下列填空.
在△ABC中, AB=AC时,
(1)∵AD ⊥ BC,
∴∠_____ = ∠_____,____= ____.
(2) ∵AD是中线,
∴____⊥____ ,∠_____=∠_____.
(3) ∵AD是角平分线,
∴____ ⊥____ ,_____=_____.
A
B
C
D
(
(
1
2
1
2
BD
CD
AD
BC
1
2
AD
BC
BD
CD
画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高,看看它们是否重合?
“三线合一”的操作
思考:建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道为什么吗?
等腰三角形一个角为75°,它的另外两个角为
____ __;
牛刀小试
75°, 30°
52.5°, 52.5°
已知:如图,在△ABC中,AB=AC,点D,E在边BC 上,且AD=AE.求证:BD=CE.
F
证明 : 作AF⊥BC,垂足为点F,
则AF是等腰△ABC和等腰△ADE底边上的高,也是底边上的中线.
∴ BF=CF,
DF=EF,
∴ BF-DF=CF-EF,
即 BD=CE.
方法总结:在等腰三角形有关计算或证明中,会遇到一些添加辅助线的问题,其顶角平分线、底边上的高、底边上的中线是常见的辅助线.
勇攀高峰
课堂小结
等腰三角形的性质
等边对等角
三线合一
注意是指同一个三角形中
注意是指顶角的平分线,底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.
课后作业
如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=30°.求∠ADC和∠CAD的度数.
谢 谢!
同课章节目录
