人教版六年级上册数学 第1单元 分数乘法 复习课件(共20张ppt)
文档属性
| 名称 | 人教版六年级上册数学 第1单元 分数乘法 复习课件(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 334.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 19:56:13 | ||
图片预览







文档简介
第1单元 分数乘法 复习课件
1、你采用什么方式整理复习的?
2、这一单元里你整理的内容有哪些?
你所交流的那部份的内容有哪些?
重难点是什么?
3、你觉得有哪些地方需要提醒大家的?
创设情境,引入新课
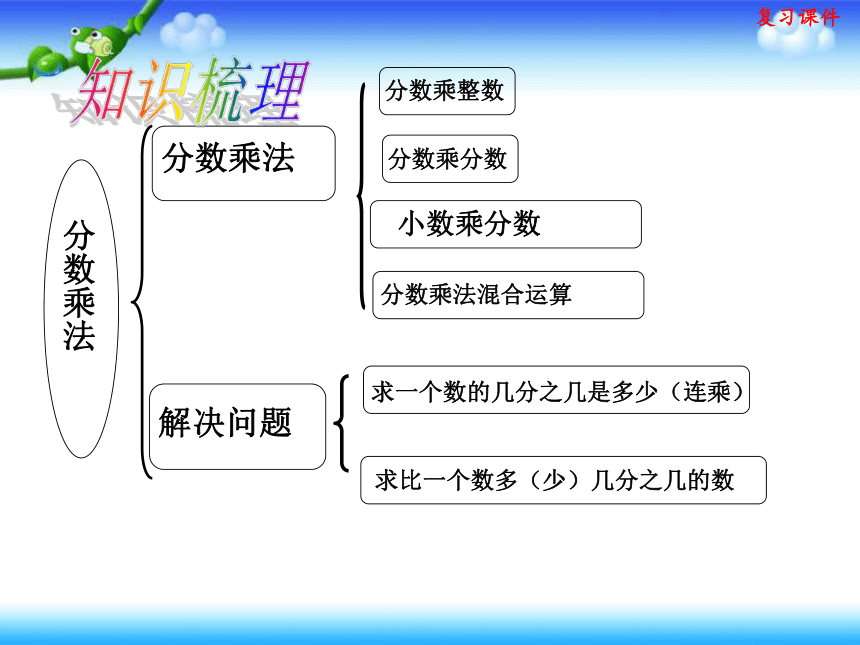
分数乘法
解决问题
分数乘法
分数乘整数
分数乘分数
分数乘法混合运算
求一个数的几分之几是多少(连乘)
求比一个数多(少)几分之几的数
知识梳理
小数乘分数
一、分数乘法?
(一)分数乘法的意义:?
1、分数乘整数与整数乘法的意义相同。都是求几个相同加数的和的简便运算。例如:65×5表示求5个65的和是多少?1/3×5表示求5个1/3的和是多少??
2、一个数乘分数的意义是求一个数的几分之几是多少。??例如:1/3×4/7表示求1/3的4/7是多少。4×3/8表示求4的3/8是多少。
(二)分数乘法的计算法则:?
1、分数与整数相乘:分子与整数相乘的积做分子,分母不变。(整数和分母约分)?
2、分数与分数相乘:用分子相乘的积做分子,分母相乘的积做分母。注意:当带分数进行乘法计算时,要先把带分数化成假分数再进行计算。?
3、为了计算简便,能约分的要先约分,再计算。(尽量约分,不会约分的就不约,常考的质因数有11×11=121;13×13=169;17×17=289;19×19=361)?
4、小数乘分数,可以先把小数化为分数,也可以把分数化成小数再计算(建议把小数化分数再计算)。
(三)?乘法中比较大小的规律?
一个数(0除外)乘大于1的数,积大于这个数。?
一个数(0除外)乘小于1的数(0除外),积小于这个数。
一个数(0除外)乘1,积等于这个数。?
(四)分数混合运算的运算顺序和整数的运算顺序相同。整数乘法的交换律、结合律和分配律,对于分数乘法也同样适用。???
乘法交换律:?a?×?b?=?b?×?a?
乘法结合律:(?a?×?b?)×c?=?a?×?(?b?×?c?)???
乘法分配律:(?a?+?b?)×c?=?a?c?+?b?c?
?二、分数乘法的解决问题(已知单位“1”的量(用乘法),即求单位“1”的几分之几是多少)?
1、画线段图:
(1)两个量的关系:画两条线段图,先画单位一的量,注意两条线段的左边要对齐。
(2)部分和整体的关系:画一条线段图。?
说出把哪个数量看作单位“1”。
(1)棉田的面积占全村耕地面积的 。
(2)故事书的本数比科技书多 。
(3)飞机速度的 相当于汽车速度。
5
2
3
1
5
1
自主探究
1.计算下面各题,说一说分数乘法是怎样进行的。
×5
24×
×
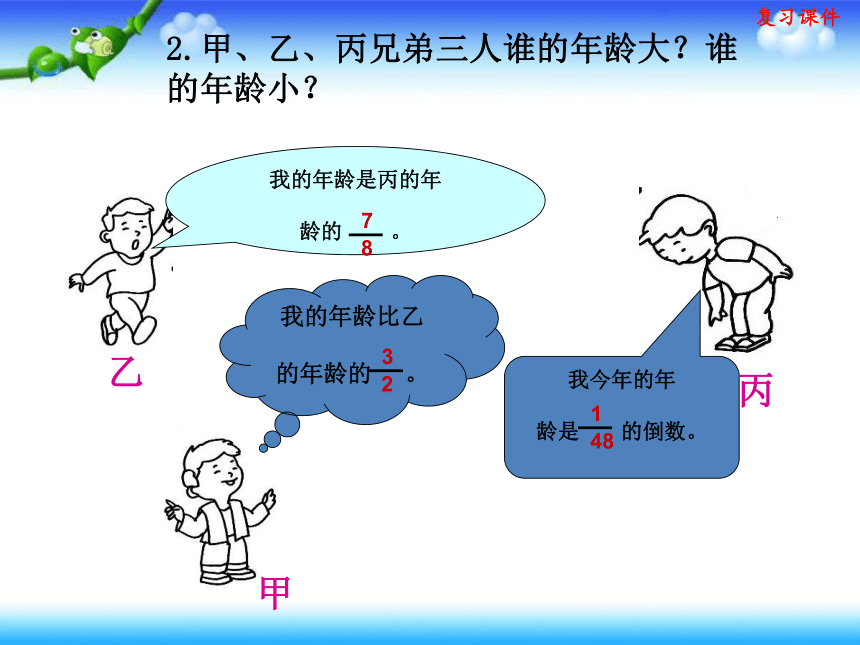
2.甲、乙、丙兄弟三人谁的年龄大?谁的年龄小?
我的年龄比乙
的年龄的 。
我的年龄是丙的年
龄的 。
我今年的年
龄是 的倒数。
乙
甲
丙
8
7
2
3
48
1
3.美术小组有25人,美术小组的人数比航模小组多 。航模小组有多少人?
1
4
画线段图:
航模小组:
美术小组:
比航模小组多
1
4
25人
?
讨论:找出这一题的等量关系式。
1.芳芳的妈妈买回来一卷丝带,长24
米,她第一周用了 ,第二周用了
这卷丝带的 ,
4
1
6
1
?
巩固练习
你能提出怎样的问题?
芳芳的妈妈买回来一卷丝带,长24米,她第一周用了 ,第二周用了 。
4
1
6
1
米
1、两周一共用去多少米?
2、还剩下多少米?
3、哪周用去的多?多多少?
2.下面的计算对吗?如果不对错在哪里?
5
3
+
5
2
×
4
1
=
1
×
4
1
=
4
1
9
2
+
8
5
-
8
5
+
9
2
=
0
0
-
0
=
(错)
(错)
3
2
9米长的绳子用去 ,用去多少米?
9米长的绳子用去 米,还剩多少米?
3
2
9米长的绳子用去 ,还剩全长的几分之几?
3
2
正确的为:9× (1- )
3
2
√
×
1-
3
2
3
2
列式为9×
3
2
列式为9-
3
2
列式为9×(1- )
3
2
9米长的绳子用去 ,还剩多少米?
√
3
2
列式为9×
×
3、看图列式,不解答。
4
1
4、某厂计划生产化肥480万吨,实际比
计划多 ,实际生产化肥多少万吨?
5、我校去年计划用水2500立方米,实际比计划少 ,我校去年实际用水多少立方米? ,
5
2
4
1
4、某厂计划生产化肥480万吨,实际比
计划多 ,实际生产化肥多少万吨?
5、我校去年计划用水2500立方米,实际比计划少 ,我校去年实际用水多少立方米? ,
5
2
480× +480=600(吨)
4
1
2500-2500× =1500(立方米)
5
2
6、星河小学召开运动会,参加长跑的有24人。参加短跑的人数是长跑的2倍,参加跳高的人数是长跑的5/6,参加跳远的人数是长跑的9/8。先估计参加哪种比赛的人最多,参加哪种比赛的人最少,再计算出参加三种比赛的各有多少人。
6、星河小学召开运动会,参加长跑的有24人。参加短跑的人数是长跑的2倍,参加跳高的人数是长跑的5/6,参加跳远的人数是长跑的9/8。先估计参加哪种比赛的人最多,参加哪种比赛的人最少,再计算出参加三种比赛的各有多少人。
短跑最多,跳高最少。
短跑:24×2=48(人)
跳高:24×5/6=20(人)
跳远:24×9/8=27(人)
谢 谢
1、你采用什么方式整理复习的?
2、这一单元里你整理的内容有哪些?
你所交流的那部份的内容有哪些?
重难点是什么?
3、你觉得有哪些地方需要提醒大家的?
创设情境,引入新课
分数乘法
解决问题
分数乘法
分数乘整数
分数乘分数
分数乘法混合运算
求一个数的几分之几是多少(连乘)
求比一个数多(少)几分之几的数
知识梳理
小数乘分数
一、分数乘法?
(一)分数乘法的意义:?
1、分数乘整数与整数乘法的意义相同。都是求几个相同加数的和的简便运算。例如:65×5表示求5个65的和是多少?1/3×5表示求5个1/3的和是多少??
2、一个数乘分数的意义是求一个数的几分之几是多少。??例如:1/3×4/7表示求1/3的4/7是多少。4×3/8表示求4的3/8是多少。
(二)分数乘法的计算法则:?
1、分数与整数相乘:分子与整数相乘的积做分子,分母不变。(整数和分母约分)?
2、分数与分数相乘:用分子相乘的积做分子,分母相乘的积做分母。注意:当带分数进行乘法计算时,要先把带分数化成假分数再进行计算。?
3、为了计算简便,能约分的要先约分,再计算。(尽量约分,不会约分的就不约,常考的质因数有11×11=121;13×13=169;17×17=289;19×19=361)?
4、小数乘分数,可以先把小数化为分数,也可以把分数化成小数再计算(建议把小数化分数再计算)。
(三)?乘法中比较大小的规律?
一个数(0除外)乘大于1的数,积大于这个数。?
一个数(0除外)乘小于1的数(0除外),积小于这个数。
一个数(0除外)乘1,积等于这个数。?
(四)分数混合运算的运算顺序和整数的运算顺序相同。整数乘法的交换律、结合律和分配律,对于分数乘法也同样适用。???
乘法交换律:?a?×?b?=?b?×?a?
乘法结合律:(?a?×?b?)×c?=?a?×?(?b?×?c?)???
乘法分配律:(?a?+?b?)×c?=?a?c?+?b?c?
?二、分数乘法的解决问题(已知单位“1”的量(用乘法),即求单位“1”的几分之几是多少)?
1、画线段图:
(1)两个量的关系:画两条线段图,先画单位一的量,注意两条线段的左边要对齐。
(2)部分和整体的关系:画一条线段图。?
说出把哪个数量看作单位“1”。
(1)棉田的面积占全村耕地面积的 。
(2)故事书的本数比科技书多 。
(3)飞机速度的 相当于汽车速度。
5
2
3
1
5
1
自主探究
1.计算下面各题,说一说分数乘法是怎样进行的。
×5
24×
×
2.甲、乙、丙兄弟三人谁的年龄大?谁的年龄小?
我的年龄比乙
的年龄的 。
我的年龄是丙的年
龄的 。
我今年的年
龄是 的倒数。
乙
甲
丙
8
7
2
3
48
1
3.美术小组有25人,美术小组的人数比航模小组多 。航模小组有多少人?
1
4
画线段图:
航模小组:
美术小组:
比航模小组多
1
4
25人
?
讨论:找出这一题的等量关系式。
1.芳芳的妈妈买回来一卷丝带,长24
米,她第一周用了 ,第二周用了
这卷丝带的 ,
4
1
6
1
?
巩固练习
你能提出怎样的问题?
芳芳的妈妈买回来一卷丝带,长24米,她第一周用了 ,第二周用了 。
4
1
6
1
米
1、两周一共用去多少米?
2、还剩下多少米?
3、哪周用去的多?多多少?
2.下面的计算对吗?如果不对错在哪里?
5
3
+
5
2
×
4
1
=
1
×
4
1
=
4
1
9
2
+
8
5
-
8
5
+
9
2
=
0
0
-
0
=
(错)
(错)
3
2
9米长的绳子用去 ,用去多少米?
9米长的绳子用去 米,还剩多少米?
3
2
9米长的绳子用去 ,还剩全长的几分之几?
3
2
正确的为:9× (1- )
3
2
√
×
1-
3
2
3
2
列式为9×
3
2
列式为9-
3
2
列式为9×(1- )
3
2
9米长的绳子用去 ,还剩多少米?
√
3
2
列式为9×
×
3、看图列式,不解答。
4
1
4、某厂计划生产化肥480万吨,实际比
计划多 ,实际生产化肥多少万吨?
5、我校去年计划用水2500立方米,实际比计划少 ,我校去年实际用水多少立方米? ,
5
2
4
1
4、某厂计划生产化肥480万吨,实际比
计划多 ,实际生产化肥多少万吨?
5、我校去年计划用水2500立方米,实际比计划少 ,我校去年实际用水多少立方米? ,
5
2
480× +480=600(吨)
4
1
2500-2500× =1500(立方米)
5
2
6、星河小学召开运动会,参加长跑的有24人。参加短跑的人数是长跑的2倍,参加跳高的人数是长跑的5/6,参加跳远的人数是长跑的9/8。先估计参加哪种比赛的人最多,参加哪种比赛的人最少,再计算出参加三种比赛的各有多少人。
6、星河小学召开运动会,参加长跑的有24人。参加短跑的人数是长跑的2倍,参加跳高的人数是长跑的5/6,参加跳远的人数是长跑的9/8。先估计参加哪种比赛的人最多,参加哪种比赛的人最少,再计算出参加三种比赛的各有多少人。
短跑最多,跳高最少。
短跑:24×2=48(人)
跳高:24×5/6=20(人)
跳远:24×9/8=27(人)
谢 谢
