人教版九年级数学下册 26.1 反比例函数 同步测试题(word解析版)
文档属性
| 名称 | 人教版九年级数学下册 26.1 反比例函数 同步测试题(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 92.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 15:57:14 | ||
图片预览


文档简介
104902001069340012319000026.1 反比例函数 同步测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 下列函数中,是反比例函数的是( )
A.y=2x+1 B.y=5x C.x:y=8 D.xy=-1
?
2. 反比例函数图象经过点(-2,?3),则该反比例函数解析式为( )
A.y=-6x B.y=6x C.y=x6 D.y=-x6
?
3. 对于反比例函数y=5x,下列结论中正确的是( )
A.y取正值
B.每个象限内,y随x的增大而增大
C.每个象限内,y随x的增大而减小
D.y取负值
?
4. 如图,反比例函数y=kx(k≠0)的图象经过点B(-2,?1),则k的值为( )
A.2 B.-2 C.±2 D.-4
?
5. 已知反比例函数y=6x,当1 A.06 D.2?
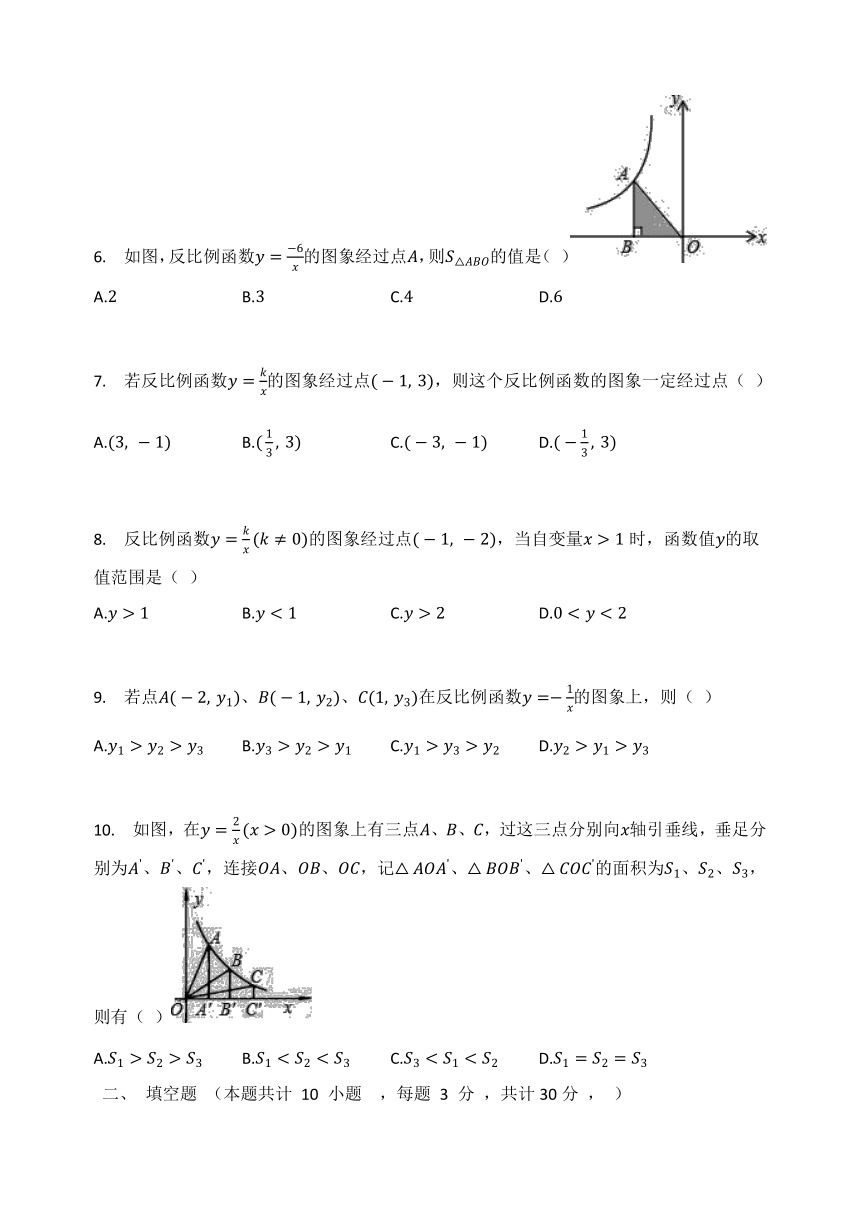
6. 如图,反比例函数y=-6x的图象经过点A,则S△ABO的值是( )
A.2 B.3 C.4 D.6
?
7. 若反比例函数y=kx的图象经过点(-1,?3),则这个反比例函数的图象一定经过点( )
A.(3,?-1) B.(13,?3) C.(-3,?-1) D.(-13,?3)
?
8. 反比例函数y=kx(k≠0)的图象经过点(-1,?-2),当自变量x>1时,函数值y的取值范围是( )
A.y>1 B.y<1 C.y>2 D.0?
9. 若点A(-2,?y1)、B(-1,?y2)、C(1,?y3)在反比例函数y=-1x的图象上,则( )
A.y1>y2>y3 B.y3>y2>y1 C.y1>y3>y2 D.y2>y1>y3
?
10. 如图,在y=2x(x>0)的图象上有三点A、B、C,过这三点分别向x轴引垂线,垂足分别为A'、B'、C',连接OA、OB、OC,记△AOA'、△BOB'、△COC'的面积为S1、S2、S3,则有( )
A.S1>S2>S3 B.S1 二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 过反比例函数上的一点分别作x轴与y轴的垂线,若与坐标轴围成的矩形的面积为4,则反比例函数的解析式为________.
?
12. 反比例函数y=kx经过(-6,?2),则k=________.
?
13. 若反比例函数y=-mx的图象经过点(-3,?-4),则m=________.
?
14. 点(-3,?2)在一个反比例函数的图象上,则这个反比例函数的解析式是________.
?
15. 已知点A(2,?m)在函数y=2x的图象上,那么m=________.
?
16. 在函数y=(m2-m)xm2-2中,当m=________时,它是反比例函数.
?
17. 一个反比例函数图象过点A(-2,?-3),则这个反比例函数的解析式是________.
?
18. 如图,符合图象的解析式是________.(填序号)
①y=2x? ②y=-2x? ③y=2x和y=-2x? ④y=2|x|.
?
19. 已知反比例函数图象A,B,C对应各自反比例函数系数k1,k2,k3;则k1,k2,k3的大小关系________.
?
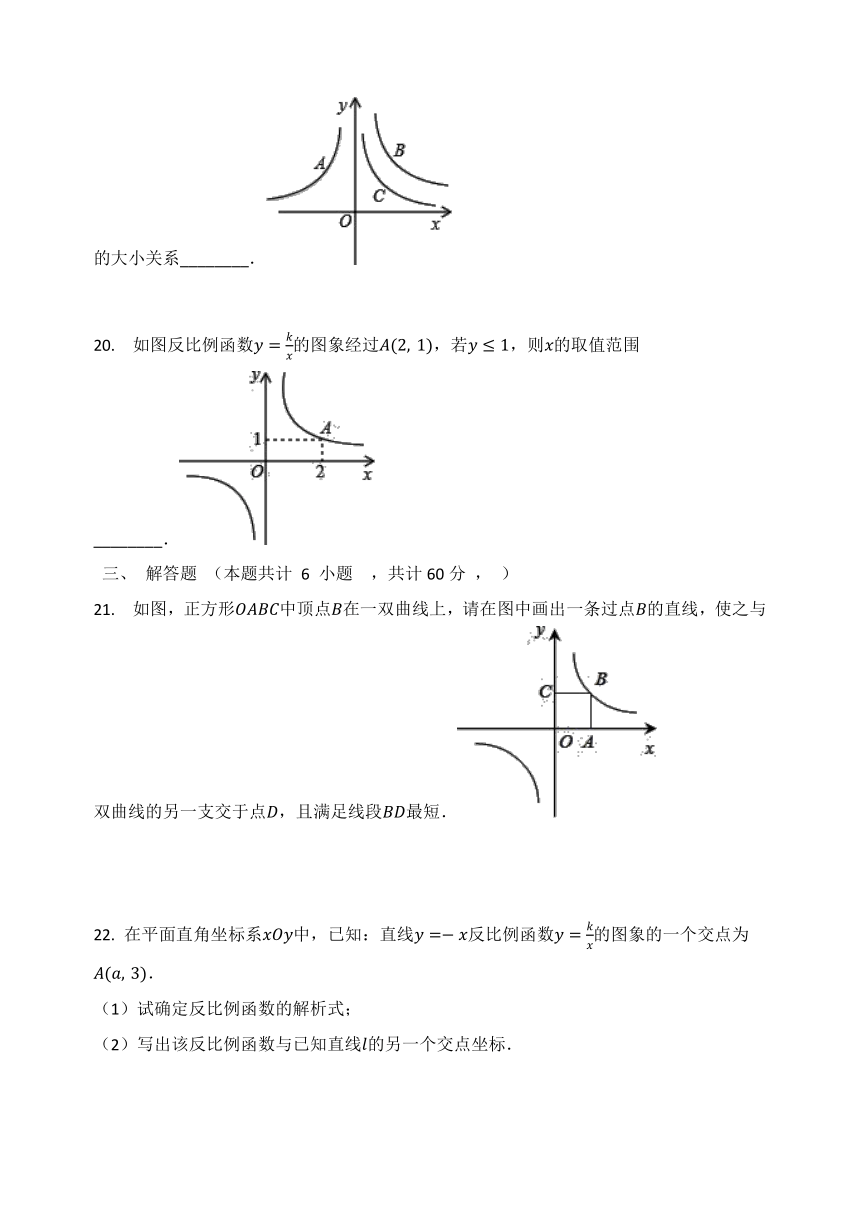
20. 如图反比例函数y=kx的图象经过A(2,?1),若y≤1,则x的取值范围________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 如图,正方形OABC中顶点B在一双曲线上,请在图中画出一条过点B的直线,使之与双曲线的另一支交于点D,且满足线段BD最短.
?
22. 在平面直角坐标系xOy中,已知:直线y=-x反比例函数y=kx的图象的一个交点为A(a,?3).
(1)试确定反比例函数的解析式;
(2)写出该反比例函数与已知直线l的另一个交点坐标.
?
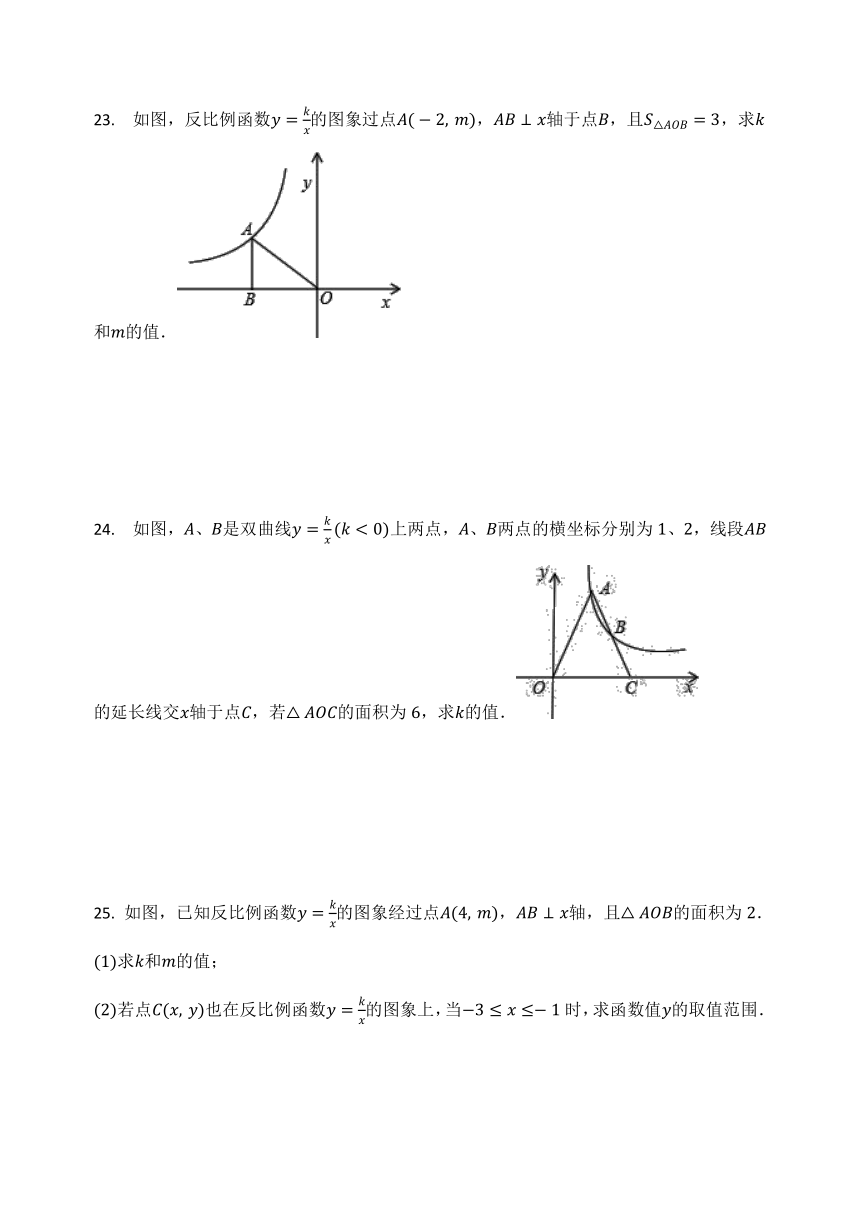
23. 如图,反比例函数y=kx的图象过点A(-2,?m),AB⊥x轴于点B,且S△AOB=3,求k和m的值.
?
24. 如图,A、B是双曲线y=kx(k<0)上两点,A、B两点的横坐标分别为1、2,线段AB的延长线交x轴于点C,若△AOC的面积为6,求k的值.
?
25. 如图,已知反比例函数y=kx的图象经过点A(4,?m),AB⊥x轴,且△AOB的面积为2.
(1)求k和m的值;
(2)若点C(x,?y)也在反比例函数y=kx的图象上,当-3≤x≤-1时,求函数值y的取值范围.
?
26. 如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=(n为常数,且n≠0)的图象在第二象限交于点A.CD⊥x轴,垂足为D,若OB=20A=30D=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤的解集.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
D
【解答】
解:A、该函数属于一次函数,故本选项错误;
B、该函数属于正比例函数,故本选项错误;
C、由原式得到:y=x8,该函数属于正比例函数,故本选项错误;
D、由原式得到:y=-1x,符合反比例函数的定义,故本选项正确.
故选:D.
2.
【答案】
A
【解答】
解:设反比例函数解析式为y=kx,
∵ 反比例函数图象经过点(-2,?3),
∴ k=-2×3=-6,
∴ 反比例函数解析式为y=-6x,
故选:A.
3.
【答案】
C
【解答】
解:y可取除0外的任意值,故A、D错误;
每个象限内,y随x的增大而减小,故B错误;C正确;
故选C.
4.
【答案】
B
【解答】
解:设y=kx,
把(-2,?1)代入,得
k=xy=-2,
故选B.
5.
【答案】
D
【解答】
∵ k=6>0,
∴ 在每个象限内y随x的增大而减小,
又∵ 当x=1时,y=6,
当x=3时,y=2,
∴ 当16.
【答案】
B
【解答】
解:由函数的意义,得
k=xy=-6,
S△ABO=|xy|2=|-6|2=3,
故选:B.
7.
【答案】
A
【解答】
解:∵ 反比例函数y=kx的图象经过点(-1,?3),
∴ k=-3.
A、∵ 3×(-1)=-3,∴ 此点在反比例函数的图象上,故本选项正确;
B、∵ 13×3=1≠-3,∴ 此点不在反比例函数的图象上,故本选项错误;
C、∵ (-3)×(-1)=3≠-3,∴ 此点不在反比例函数的图象上,故本选项错误;
D、∵ (-13)×3=-1≠-3,∴ 此点不在反比例函数的图象上,故本选项错误.
故选A.
8.
【答案】
D
【解答】
解:∵ 反比例函数y=kx(k≠0)的图象经过点(-1,?-2),
∴ k=-1×(-2)=2,
∴ 在每一象限,y随着x的增大而减小,
∴ 当x=1时,y=2,
∴ 当x>1时,0故选D.
9.
【答案】
D
【解答】
解:∵ 点A(-2,?y1)、B(-1,?y2)、C(1,?y3)在反比例函数y=-1x的图象上,
∴ y1=-1-2=12,y2=-1-1=1,y3=-11=-1,
∵ -1<12<1,
∴ y2>y1>y3.
故选D.
10.
【答案】
D
【解答】
解:由题意得:在y=2x(x>0)的图象上有三点A、B、C,过这三点分别向x轴引垂线,垂足分别为A'、B'、C',
则S1=S2=S3=|k|=2.
故选D.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
y=4x或y=-4x
【解答】
解:由题意得:S=|k|=4;
k=±4.
故答案为y=4x或y=-4x.
12.
【答案】
-12
【解答】
解:∵ 反比例函数y=kx经过(-6,?2),
∴ 2=k-6,解得k=-12.
故答案为:-12.
13.
【答案】
-12
【解答】
解:把(-3,?-4)代入反比例函数y=-mx,
得-4=-m-3,
m=-12,
故答案为:-12.
14.
【答案】
y=-6x
【解答】
解:设反比例函数解析式y=kx,
把(-3,?2)代入得k=-3×2=-6,
所以反比例函数解析式为y=-6x.
故答案为y=-6x.
15.
【答案】
1
【解答】
解:由题意得,点A(2,?m)在函数y=2x的图象上,
则2=2m,解得:m=1.
故答案为1.
16.
【答案】
-1
【解答】
解:由题意得:m2-2=-1,且m2-m≠0,
解得:m=-1,
故答案为:-1.
17.
【答案】
y=6x
【解答】
解:设这个反比例函数解析式为y=kx,
∴ k-2=-3,
解得:k=6,
∴ 这个反比例函数的解析式是y=6x.
故答案为:y=6x.
18.
【答案】
④
【解答】
解:∵ 双曲线在第一和第二象限,
∴ y>0,
∴ 应选④,
故答案为④.
19.
【答案】
k1【解答】
解:根据图象可知|k|越大,离原点越远,
则k1<0,k2>k3>0,
所以k1,k2,k3的大小关系是k1故答案为:k120.
【答案】
x≥2,x<0
【解答】
解:由图象可得,直线直线y=1上以及下方的函数图象所对应的自变量的取值为x≥2,x<0.
故答案为:x≥2,x<0.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:∵ 双曲线关于直线y=x及直线y=-x对称,而线段BD在直线y=x上,则易得∠BDD'>90?
∴ BD最短.
【解答】
解:∵ 双曲线关于直线y=x及直线y=-x对称,而线段BD在直线y=x上,则易得∠BDD'>90?
∴ BD最短.
22.
【答案】
解:(1)因为A(a,?3)在直线y=-x上,
则a=-3,即A(-3,?3),
又因为A(-3,?3)在y=kx的图象上,
可求得k=-9,
所以反比例函数的解析式为y=-9x;
(2)另一个交点坐标是(3,?-3).
【解答】
解:(1)因为A(a,?3)在直线y=-x上,
则a=-3,即A(-3,?3),
又因为A(-3,?3)在y=kx的图象上,
可求得k=-9,
所以反比例函数的解析式为y=-9x;
(2)另一个交点坐标是(3,?-3).
23.
【答案】
解:∵ S△AOB=3,
∴ 12|k|=3,
k=±6,
∵ 函数图象在第二象限,
∴ k=-6,
∴ 反比例函数解析式为y=-6x,
∵ 反比例函数y=-6x的图象过点A(-2,?m),
∴ -2m=-6,
解得:m=3.
【解答】
解:∵ S△AOB=3,
∴ 12|k|=3,
k=±6,
∵ 函数图象在第二象限,
∴ k=-6,
∴ 反比例函数解析式为y=-6x,
∵ 反比例函数y=-6x的图象过点A(-2,?m),
∴ -2m=-6,
解得:m=3.
24.
【答案】
解:作AD⊥x轴于D,BE⊥x轴于E,如图,
∵ A、B两点的横坐标分别为1、2,
∴ A(1,?k),B(2,?k2),
∴ OD=1,DE=1,AD=2BE,
∴ BE为△ADC的中位线,
∴ CE=DE=2,
∴ OC=3,
∵ △AOC的面积为6,
∴ 12?3?k=6,
∴ k=4.
【解答】
解:作AD⊥x轴于D,BE⊥x轴于E,如图,
∵ A、B两点的横坐标分别为1、2,
∴ A(1,?k),B(2,?k2),
∴ OD=1,DE=1,AD=2BE,
∴ BE为△ADC的中位线,
∴ CE=DE=2,
∴ OC=3,
∵ △AOC的面积为6,
∴ 12?3?k=6,
∴ k=4.
25.
【答案】
解:(1)∵ △AOB的面积为2,
∴ k=4,
∴ 反比例函数解析式为y=4x,
∵ A(4,?m),
∴ m=44=1;
(2)∵ 当x=-3时,y=-43;
当x=-1时,y=-4,
又∵ 反比例函数y=4x在x<0时,y随x的增大而减小,
∴ 当-3≤x≤-1时,y的取值范围为-4≤y≤-43.
【解答】
解:(1)∵ △AOB的面积为2,
∴ k=4,
∴ 反比例函数解析式为y=4x,
∵ A(4,?m),
∴ m=44=1;
(2)∵ 当x=-3时,y=-43;
当x=-1时,y=-4,
又∵ 反比例函数y=4x在x<0时,y随x的增大而减小,
∴ 当-3≤x≤-1时,y的取值范围为-4≤y≤-43.
26.
【答案】
(1)y=-80x y=-2x+12
(2)S△CDE=140;
(3)x≥10,或-4≤x<0
【解答】
(1)由已知,OA=6,OB=12,OD=4
CD⊥x轴
..OBIICD
△ABO-△ACD
∴ OAAD=OBCD
∴ . 610=12CD
小CD=20
点C坐标为-4,20
n=xy=-80
…反比例函数解析式为:y=-80x
把点Aξ,0,B0,12代入y=kx+b得:
0=6k+bb=12
解得:k=-2b=12
…一次函数解析式为:y=-2x+12
(2)当-80x=-2x+12时,解得
x1=10,x2=-4
当x=10时,y=-8
…点E坐标为10,-8
.S△CDE=S△CDA+S△EDA=12×20×10+12×8×10=140
(3)不等式kx+b≤nx,从函数图象上看,表示一次函数图象不低于反比例函数图象
…由图象得,x≥10,或-4≤x<0
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 下列函数中,是反比例函数的是( )
A.y=2x+1 B.y=5x C.x:y=8 D.xy=-1
?
2. 反比例函数图象经过点(-2,?3),则该反比例函数解析式为( )
A.y=-6x B.y=6x C.y=x6 D.y=-x6
?
3. 对于反比例函数y=5x,下列结论中正确的是( )
A.y取正值
B.每个象限内,y随x的增大而增大
C.每个象限内,y随x的增大而减小
D.y取负值
?
4. 如图,反比例函数y=kx(k≠0)的图象经过点B(-2,?1),则k的值为( )
A.2 B.-2 C.±2 D.-4
?
5. 已知反比例函数y=6x,当1
6. 如图,反比例函数y=-6x的图象经过点A,则S△ABO的值是( )
A.2 B.3 C.4 D.6
?
7. 若反比例函数y=kx的图象经过点(-1,?3),则这个反比例函数的图象一定经过点( )
A.(3,?-1) B.(13,?3) C.(-3,?-1) D.(-13,?3)
?
8. 反比例函数y=kx(k≠0)的图象经过点(-1,?-2),当自变量x>1时,函数值y的取值范围是( )
A.y>1 B.y<1 C.y>2 D.0
9. 若点A(-2,?y1)、B(-1,?y2)、C(1,?y3)在反比例函数y=-1x的图象上,则( )
A.y1>y2>y3 B.y3>y2>y1 C.y1>y3>y2 D.y2>y1>y3
?
10. 如图,在y=2x(x>0)的图象上有三点A、B、C,过这三点分别向x轴引垂线,垂足分别为A'、B'、C',连接OA、OB、OC,记△AOA'、△BOB'、△COC'的面积为S1、S2、S3,则有( )
A.S1>S2>S3 B.S1
11. 过反比例函数上的一点分别作x轴与y轴的垂线,若与坐标轴围成的矩形的面积为4,则反比例函数的解析式为________.
?
12. 反比例函数y=kx经过(-6,?2),则k=________.
?
13. 若反比例函数y=-mx的图象经过点(-3,?-4),则m=________.
?
14. 点(-3,?2)在一个反比例函数的图象上,则这个反比例函数的解析式是________.
?
15. 已知点A(2,?m)在函数y=2x的图象上,那么m=________.
?
16. 在函数y=(m2-m)xm2-2中,当m=________时,它是反比例函数.
?
17. 一个反比例函数图象过点A(-2,?-3),则这个反比例函数的解析式是________.
?
18. 如图,符合图象的解析式是________.(填序号)
①y=2x? ②y=-2x? ③y=2x和y=-2x? ④y=2|x|.
?
19. 已知反比例函数图象A,B,C对应各自反比例函数系数k1,k2,k3;则k1,k2,k3的大小关系________.
?
20. 如图反比例函数y=kx的图象经过A(2,?1),若y≤1,则x的取值范围________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 如图,正方形OABC中顶点B在一双曲线上,请在图中画出一条过点B的直线,使之与双曲线的另一支交于点D,且满足线段BD最短.
?
22. 在平面直角坐标系xOy中,已知:直线y=-x反比例函数y=kx的图象的一个交点为A(a,?3).
(1)试确定反比例函数的解析式;
(2)写出该反比例函数与已知直线l的另一个交点坐标.
?
23. 如图,反比例函数y=kx的图象过点A(-2,?m),AB⊥x轴于点B,且S△AOB=3,求k和m的值.
?
24. 如图,A、B是双曲线y=kx(k<0)上两点,A、B两点的横坐标分别为1、2,线段AB的延长线交x轴于点C,若△AOC的面积为6,求k的值.
?
25. 如图,已知反比例函数y=kx的图象经过点A(4,?m),AB⊥x轴,且△AOB的面积为2.
(1)求k和m的值;
(2)若点C(x,?y)也在反比例函数y=kx的图象上,当-3≤x≤-1时,求函数值y的取值范围.
?
26. 如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=(n为常数,且n≠0)的图象在第二象限交于点A.CD⊥x轴,垂足为D,若OB=20A=30D=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤的解集.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
D
【解答】
解:A、该函数属于一次函数,故本选项错误;
B、该函数属于正比例函数,故本选项错误;
C、由原式得到:y=x8,该函数属于正比例函数,故本选项错误;
D、由原式得到:y=-1x,符合反比例函数的定义,故本选项正确.
故选:D.
2.
【答案】
A
【解答】
解:设反比例函数解析式为y=kx,
∵ 反比例函数图象经过点(-2,?3),
∴ k=-2×3=-6,
∴ 反比例函数解析式为y=-6x,
故选:A.
3.
【答案】
C
【解答】
解:y可取除0外的任意值,故A、D错误;
每个象限内,y随x的增大而减小,故B错误;C正确;
故选C.
4.
【答案】
B
【解答】
解:设y=kx,
把(-2,?1)代入,得
k=xy=-2,
故选B.
5.
【答案】
D
【解答】
∵ k=6>0,
∴ 在每个象限内y随x的增大而减小,
又∵ 当x=1时,y=6,
当x=3时,y=2,
∴ 当1
【答案】
B
【解答】
解:由函数的意义,得
k=xy=-6,
S△ABO=|xy|2=|-6|2=3,
故选:B.
7.
【答案】
A
【解答】
解:∵ 反比例函数y=kx的图象经过点(-1,?3),
∴ k=-3.
A、∵ 3×(-1)=-3,∴ 此点在反比例函数的图象上,故本选项正确;
B、∵ 13×3=1≠-3,∴ 此点不在反比例函数的图象上,故本选项错误;
C、∵ (-3)×(-1)=3≠-3,∴ 此点不在反比例函数的图象上,故本选项错误;
D、∵ (-13)×3=-1≠-3,∴ 此点不在反比例函数的图象上,故本选项错误.
故选A.
8.
【答案】
D
【解答】
解:∵ 反比例函数y=kx(k≠0)的图象经过点(-1,?-2),
∴ k=-1×(-2)=2,
∴ 在每一象限,y随着x的增大而减小,
∴ 当x=1时,y=2,
∴ 当x>1时,0
9.
【答案】
D
【解答】
解:∵ 点A(-2,?y1)、B(-1,?y2)、C(1,?y3)在反比例函数y=-1x的图象上,
∴ y1=-1-2=12,y2=-1-1=1,y3=-11=-1,
∵ -1<12<1,
∴ y2>y1>y3.
故选D.
10.
【答案】
D
【解答】
解:由题意得:在y=2x(x>0)的图象上有三点A、B、C,过这三点分别向x轴引垂线,垂足分别为A'、B'、C',
则S1=S2=S3=|k|=2.
故选D.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
y=4x或y=-4x
【解答】
解:由题意得:S=|k|=4;
k=±4.
故答案为y=4x或y=-4x.
12.
【答案】
-12
【解答】
解:∵ 反比例函数y=kx经过(-6,?2),
∴ 2=k-6,解得k=-12.
故答案为:-12.
13.
【答案】
-12
【解答】
解:把(-3,?-4)代入反比例函数y=-mx,
得-4=-m-3,
m=-12,
故答案为:-12.
14.
【答案】
y=-6x
【解答】
解:设反比例函数解析式y=kx,
把(-3,?2)代入得k=-3×2=-6,
所以反比例函数解析式为y=-6x.
故答案为y=-6x.
15.
【答案】
1
【解答】
解:由题意得,点A(2,?m)在函数y=2x的图象上,
则2=2m,解得:m=1.
故答案为1.
16.
【答案】
-1
【解答】
解:由题意得:m2-2=-1,且m2-m≠0,
解得:m=-1,
故答案为:-1.
17.
【答案】
y=6x
【解答】
解:设这个反比例函数解析式为y=kx,
∴ k-2=-3,
解得:k=6,
∴ 这个反比例函数的解析式是y=6x.
故答案为:y=6x.
18.
【答案】
④
【解答】
解:∵ 双曲线在第一和第二象限,
∴ y>0,
∴ 应选④,
故答案为④.
19.
【答案】
k1
解:根据图象可知|k|越大,离原点越远,
则k1<0,k2>k3>0,
所以k1,k2,k3的大小关系是k1
【答案】
x≥2,x<0
【解答】
解:由图象可得,直线直线y=1上以及下方的函数图象所对应的自变量的取值为x≥2,x<0.
故答案为:x≥2,x<0.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:∵ 双曲线关于直线y=x及直线y=-x对称,而线段BD在直线y=x上,则易得∠BDD'>90?
∴ BD最短.
【解答】
解:∵ 双曲线关于直线y=x及直线y=-x对称,而线段BD在直线y=x上,则易得∠BDD'>90?
∴ BD最短.
22.
【答案】
解:(1)因为A(a,?3)在直线y=-x上,
则a=-3,即A(-3,?3),
又因为A(-3,?3)在y=kx的图象上,
可求得k=-9,
所以反比例函数的解析式为y=-9x;
(2)另一个交点坐标是(3,?-3).
【解答】
解:(1)因为A(a,?3)在直线y=-x上,
则a=-3,即A(-3,?3),
又因为A(-3,?3)在y=kx的图象上,
可求得k=-9,
所以反比例函数的解析式为y=-9x;
(2)另一个交点坐标是(3,?-3).
23.
【答案】
解:∵ S△AOB=3,
∴ 12|k|=3,
k=±6,
∵ 函数图象在第二象限,
∴ k=-6,
∴ 反比例函数解析式为y=-6x,
∵ 反比例函数y=-6x的图象过点A(-2,?m),
∴ -2m=-6,
解得:m=3.
【解答】
解:∵ S△AOB=3,
∴ 12|k|=3,
k=±6,
∵ 函数图象在第二象限,
∴ k=-6,
∴ 反比例函数解析式为y=-6x,
∵ 反比例函数y=-6x的图象过点A(-2,?m),
∴ -2m=-6,
解得:m=3.
24.
【答案】
解:作AD⊥x轴于D,BE⊥x轴于E,如图,
∵ A、B两点的横坐标分别为1、2,
∴ A(1,?k),B(2,?k2),
∴ OD=1,DE=1,AD=2BE,
∴ BE为△ADC的中位线,
∴ CE=DE=2,
∴ OC=3,
∵ △AOC的面积为6,
∴ 12?3?k=6,
∴ k=4.
【解答】
解:作AD⊥x轴于D,BE⊥x轴于E,如图,
∵ A、B两点的横坐标分别为1、2,
∴ A(1,?k),B(2,?k2),
∴ OD=1,DE=1,AD=2BE,
∴ BE为△ADC的中位线,
∴ CE=DE=2,
∴ OC=3,
∵ △AOC的面积为6,
∴ 12?3?k=6,
∴ k=4.
25.
【答案】
解:(1)∵ △AOB的面积为2,
∴ k=4,
∴ 反比例函数解析式为y=4x,
∵ A(4,?m),
∴ m=44=1;
(2)∵ 当x=-3时,y=-43;
当x=-1时,y=-4,
又∵ 反比例函数y=4x在x<0时,y随x的增大而减小,
∴ 当-3≤x≤-1时,y的取值范围为-4≤y≤-43.
【解答】
解:(1)∵ △AOB的面积为2,
∴ k=4,
∴ 反比例函数解析式为y=4x,
∵ A(4,?m),
∴ m=44=1;
(2)∵ 当x=-3时,y=-43;
当x=-1时,y=-4,
又∵ 反比例函数y=4x在x<0时,y随x的增大而减小,
∴ 当-3≤x≤-1时,y的取值范围为-4≤y≤-43.
26.
【答案】
(1)y=-80x y=-2x+12
(2)S△CDE=140;
(3)x≥10,或-4≤x<0
【解答】
(1)由已知,OA=6,OB=12,OD=4
CD⊥x轴
..OBIICD
△ABO-△ACD
∴ OAAD=OBCD
∴ . 610=12CD
小CD=20
点C坐标为-4,20
n=xy=-80
…反比例函数解析式为:y=-80x
把点Aξ,0,B0,12代入y=kx+b得:
0=6k+bb=12
解得:k=-2b=12
…一次函数解析式为:y=-2x+12
(2)当-80x=-2x+12时,解得
x1=10,x2=-4
当x=10时,y=-8
…点E坐标为10,-8
.S△CDE=S△CDA+S△EDA=12×20×10+12×8×10=140
(3)不等式kx+b≤nx,从函数图象上看,表示一次函数图象不低于反比例函数图象
…由图象得,x≥10,或-4≤x<0
