冀教版九年级数学下册第二十九章直线与圆的位置关系巩固检测题(word版含答案)
文档属性
| 名称 | 冀教版九年级数学下册第二十九章直线与圆的位置关系巩固检测题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 481.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 19:10:56 | ||
图片预览



文档简介
冀教版九年级数学下第二十九章直线与圆的位置关系巩固检测题
[时间:120分钟 分值:120分]
一、选择题(本大题共16个小题,共42分.1~10小题,每小题3分;11~16小题,每小题2分.在每小题给出的四个选项中,只有一项符合题目要求)
1.已知☉O的半径为3,直线l与☉O相交,则圆心O到直线l的距离d的取值范围是( )
A.d=3
B.d>3
C.0≤d<3
D.02.在菱形ABCD中,AB=4,AC=6,对角线AC,BD相交于点O,以点O为圆心,3为半径作☉O,则A,B,C,D四个点中在☉O上的个数为( )
A.1
B.2
C.3
D.4
3.以点O为中心的量角器与三角尺ABC如图1所示摆放,直角顶点B在零刻度线所在直线DE上,且量角器与三角尺只有一个公共点P,若点P的读数为35°,则∠CBD的度数是( )
图1
A.55°
B.45°
C.35°
D.25°
4.如图2,在☉O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为
( )
图2
A.40°
B.50°
C.80°
D.100°
5.已知☉O的面积为2π,则其内接正三角形的面积为
( )
A.3
B.3
C.
D.
6.如图3,☉O内切于△ABC,切点分别为D,E,F.已知∠B=50°,∠C=60°,连接DE,DF,那么∠EDF的度数为
( )
图3
A.40°
B.55°
C.65°
D.70°
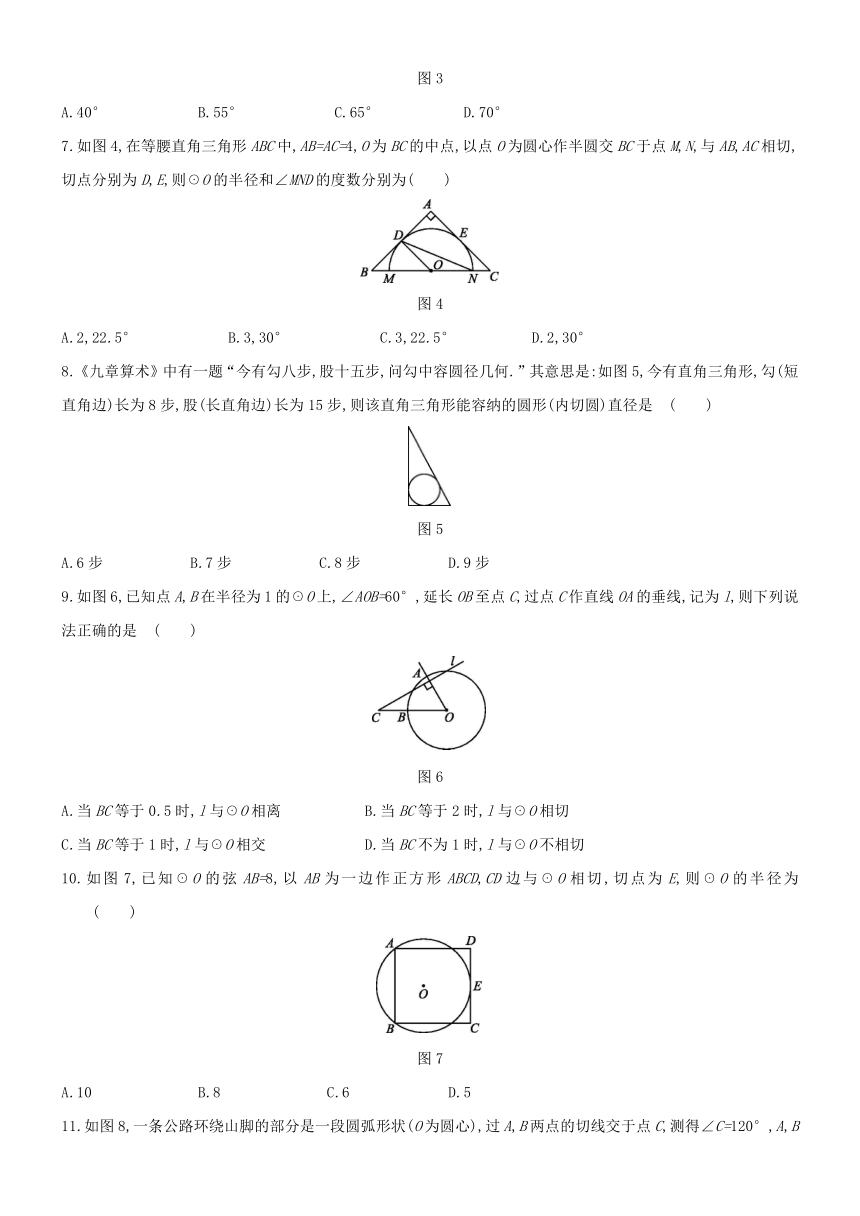
7.如图4,在等腰直角三角形ABC中,AB=AC=4,O为BC的中点,以点O为圆心作半圆交BC于点M,N,与AB,AC相切,切点分别为D,E,则☉O的半径和∠MND的度数分别为( )
图4
A.2,22.5°
B.3,30°
C.3,22.5°
D.2,30°
8.《九章算术》中有一题“今有勾八步,股十五步,问勾中容圆径几何.”其意思是:如图5,今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,则该直角三角形能容纳的圆形(内切圆)直径是
( )
图5
A.6步
B.7步
C.8步
D.9步
9.如图6,已知点A,B在半径为1的☉O上,∠AOB=60°,延长OB至点C,过点C作直线OA的垂线,记为l,则下列说法正确的是
( )
图6
A.当BC等于0.5时,l与☉O相离
B.当BC等于2时,l与☉O相切
C.当BC等于1时,l与☉O相交
D.当BC不为1时,l与☉O不相切
10.如图7,已知☉O的弦AB=8,以AB为一边作正方形ABCD,CD边与☉O相切,切点为E,则☉O的半径为
( )
图7
A.10
B.8
C.6
D.5
11.如图8,一条公路环绕山脚的部分是一段圆弧形状(O为圆心),过A,B两点的切线交于点C,测得∠C=120°,A,B两点之间的距离为60
m,则这段公路的长度是
( )
图8
A.10π
m
B.20π
m
C.10π
m
D.60
m
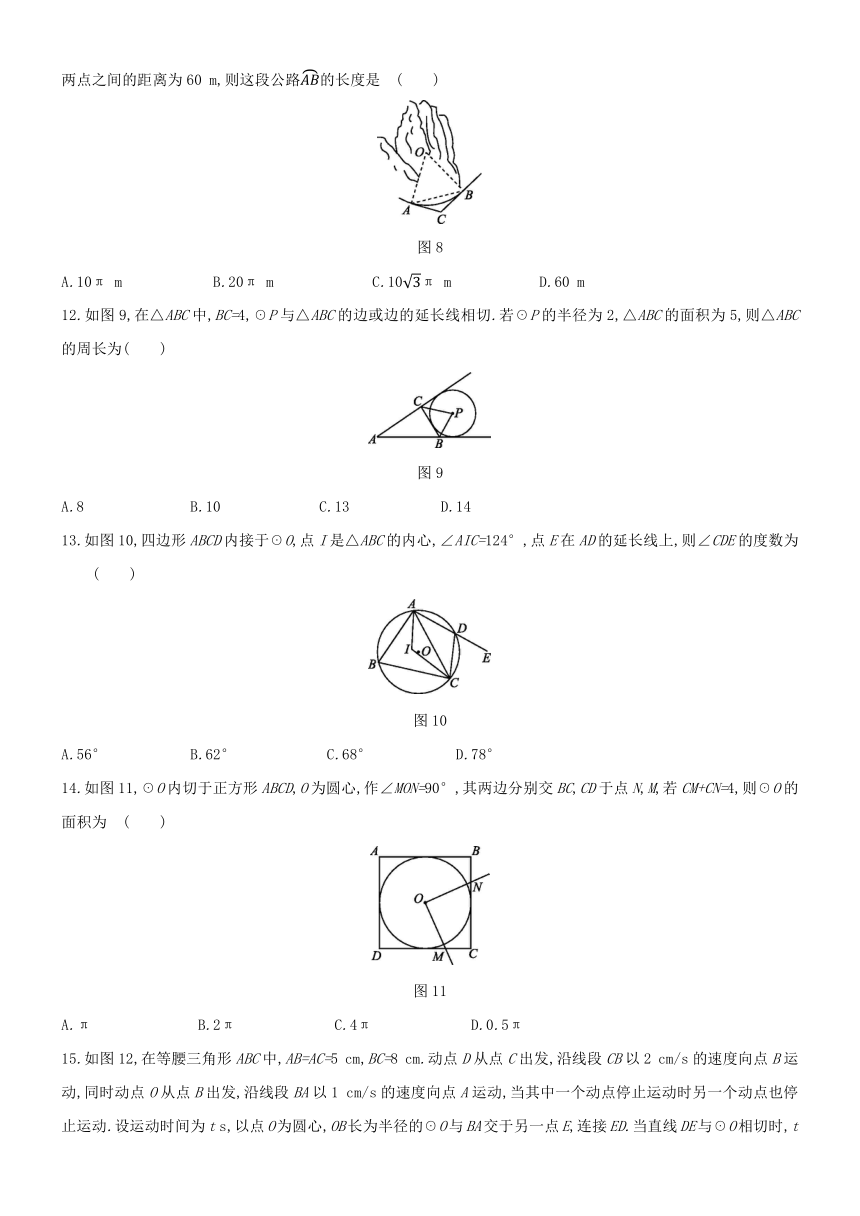
12.如图9,在△ABC中,BC=4,☉P与△ABC的边或边的延长线相切.若☉P的半径为2,△ABC的面积为5,则△ABC的周长为( )
图9
A.8
B.10
C.13
D.14
13.如图10,四边形ABCD内接于☉O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为
( )
图10
A.56°
B.62°
C.68°
D.78°
14.如图11,☉O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD于点N,M,若CM+CN=4,则☉O的面积为
( )
图11
A.π
B.2π
C.4π
D.0.5π
15.如图12,在等腰三角形ABC中,AB=AC=5
cm,BC=8
cm.动点D从点C出发,沿线段CB以2
cm/s的速度向点B运动,同时动点O从点B出发,沿线段BA以1
cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也停止运动.设运动时间为t
s,以点O为圆心,OB长为半径的☉O与BA交于另一点E,连接ED.当直线DE与☉O相切时,t的值是
( )
图12
A.
B.
C.
D.
16.如图13,边长为4的正方形ABCD内接于☉O,E是上的一动点(不与点A,B重合),F是上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:
①=;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为4+.
其中正确的是( )
图13
A.①③④
B.①②③
C.①②
D.③④
二、填空题(本大题共3个小题,共12分.17,18小题,每小题3分,19小题共6分,把答案写在题中横线上)
17.
在矩形ABCD中,AC=8
cm,∠ACB=30°,以点B为圆心,4
cm长为半径作☉B,则☉B与直线AD和CD的位置关系依次是 .?
18.如图14,AB为☉O的直径,C为☉O上一点,过点B的切线交AC的延长线于点D,E为弦AC的中点,AD=10,BD=6.若P为直径AB上的一个动点,连接EP,当△AEP是直角三角形时,AP的长为 .?
图14
19.如图15,AB是☉O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且BC是☉O的切线.
(1)若∠A=20°,则∠BCO= ;?
(2)若OA=6,OP=2,则BC的长是 .?
图15
三、解答题(本大题共7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8分)如图16,已知在Rt△ABC中,∠C=90°,AB=13,AC=5,O是AC边上的点,以点O为圆心,OC为半径作☉O.
(1)当OC=3时,判断点A、点B与☉O的位置关系;
(2)当OC=2.4时,AB与☉O有怎样的位置关系?请证明你的结论.
图16
21.(本小题满分9分)如图17,PA,PB分别与☉O相切于点A,B,AC为弦,BC为☉O的直径,若∠P=60°,PB=2
cm.
(1)求证:△PAB是等边三角形;
(2)求AC的长.
图17
22.(本小题满分9分)如图18,△ABC内接于☉O,AB是☉O的直径,☉O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.
(1)判断AF与☉O的位置关系,并说明理由;
(2)若☉O的半径为4,AF=3,求AC的长.
图18
23.(本小题满分9分)如图19,AB=BC,以BC为直径作☉O,AC交☉O于点E,过点E作EG⊥AB于点F,交CB的延长线于点G.
(1)求证:EG是☉O的切线;
(2)若GF=2,GB=4,求☉O的半径.
图19
24.(本小题满分10分)已知AB是☉O的直径,弦CD与AB相交,∠BAC=38°.
(1)如图20①,若D为的中点,求∠ABC和∠ABD的大小;
(2)如图②,过点D作☉O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
图20
25.(本小题满分10分)如图21,△ABC内接于☉O,AB为直径,∠BAC=60°,延长BA至点P,使AP=AC,作CD平分∠ACB交AB于点E,交☉O于点D,连接PC,BD.
(1)求证:PC为☉O的切线;
(2)求证:BD=AP;
(3)若PC=6,求AE的长.
图21
26.(本小题满分11分)已知OA=OB=4,∠AOB=60°,半圆A的半径为1,点C是半圆上任意一点,连接OC,把OC绕点O顺时针旋转60°到OD的位置,连接BD.
(1)如图22①,求证:AC=BD;
(2)如图22②,当OC与半圆A相切于点C时,求CD的长;
(3)直接写出△AOC面积的最大值.
图22
参考答案
1.C
2.B [解析]
如图所示,∵四边形ABCD是菱形,AC=6,
∴AC⊥BD,AO=CO=AC=3,BO=DO.
∵AB=4,
∴DO=BO===.
∵r=3=AO=CO,BO=DO=<3,
∴A,B,C,D四个点中在☉O上的个数为2.
3.C [解析]
∵AB是☉O的切线,∴∠OPB=90°.又∵∠ABC=90°,∴OP∥BC,
∴∠CBD=∠POB=35°.
4.C [解析]
∵在☉O中,CD为切线,
∴∠OCD=90°.
∵∠BCD=50°,∴∠OCB=40°.
∵OC=OB,∴∠OBC=∠OCB=40°,
∴∠AOC=80°.
5.C [解析]
由☉O的面积为2π,可求得☉O的半径为.如图,△ABC为正三角形,OC=,∠OCD=30°,过点O作OD⊥BC于点D.由cos30°=得CD=,
∴BC=,
∴S△ABC=BC2=.
6.B [解析]
如图,连接OE,OF.∵∠A+∠B+∠C=180°,∠B=50°,∠C=60°,∴∠A=70°.
∵☉O内切于△ABC,
切点分别为D,E,F,∴∠OEA=∠OFA=90°,
∴∠EOF=360°-∠A-∠OEA-∠OFA=110°,∴∠EDF=∠EOF=55°.
7.A [解析]
∵AB为☉O的切线,
∴OD⊥AB,∴∠ODB=∠A=90°.
又∠B=∠B,∴△OBD∽△CBA,
∴==,∠DOB=∠C=45°,
∴OD=CA=2,∠MND=∠DOB=22.5°.
故选A.
8.A [解析]
根据勾股定理得,斜边长为=17(步),则该直角三角形能容纳的圆形(内切圆)半径r==3(步),则直径为6步,故选A.
9.D [解析]
设直线l与OA的垂足为D.
A项,∵BC=0.5,∴OC=OB+BC=1.5.
∵∠AOB=60°,
∴∠C=30°,∴DO=OC=0.75<1,
∴l与☉O相交,故A项错误;
B项,∵BC=2,∴OC=OB+BC=3.
∵∠AOB=60°,
∴∠C=30°,∴DO=OC=1.5>1,
∴l与☉O相离,故B项错误;
C项,∵BC=1,∴OC=OB+BC=2.
∵∠AOB=60°,∴∠C=30°,∴DO=OC=1,
∴l与☉O相切,故C项错误;
D项,∵BC≠1,
∴OC=OB+BC≠2.
∵∠AOB=60°,∴∠C=30°,
∴DO=OC≠1,
∴l与☉O不相切,故D项正确.故选D.
10.D [解析]
连接EO并延长交AB于点F,连接OA.
∵CD边与☉O相切,∴OE⊥CD.
∵四边形ABCD是正方形,
∴AB∥CD,AD=AB=8,
∴EF⊥AB,
∴四边形AFED是矩形,AF=AB=4,
∴EF=AD=8.
∵OA=OE,∴OF=8-OA.
∵OA2=AF2+OF2,∴OA2=42+(8-OA)2,
解得OA=5,∴☉O的半径为5.
11.B [解析]
∵AC与BC是☉O的切线,∠C=120°,
∴∠OAC=∠OBC=90°,AC=BC,
∴∠AOB=60°.
又∵OA=OB,∴△AOB是等边三角形,
∴OA=AB=60
m.
∴公路的长度==20π(m).
12.C [解析]
如图,设切点分别为E,F,G,连接PE,PF,PG,AP.
由题意可知∠PEC=∠PFA=∠PGA=90°,
∴S△PBC=BC·PE=×4×2=4,
由切线长定理可知S△PFC+S△PBG=S△PBC=4,
∴S四边形AFPG=S△ABC+S△PFC+S△PBG+S△PBC=5+4+4=13.
由切线长定理可知S△APG=S四边形AFPG=,
∴=AG·PG,∴AG=.
由切线长定理可知CE=CF,BE=BG,
∴△ABC的周长为AC+AB+CE+BE=AC+AB+CF+BG=AF+AG=2AG=13.
13.C [解析]
∵点I是△ABC的内心,
∴∠BAC=2∠IAC,∠ACB=2∠ICA.
∵∠AIC=124°,
∴∠B=180°-(∠BAC+∠ACB)=180°-2(∠IAC+∠ICA)=180°-2(180°-∠AIC)=68°.
∵四边形ABCD内接于☉O,
∴∠CDA=180°-∠B=112°,
∴∠CDE=180°-∠CDA=68°.
14.C [解析]
如图,设☉O与正方形ABCD的边CD切于点E,与BC切于点F,连接OE,OF,
则四边形OECF是正方形,
∴CF=CE=OE=OF,∠OEM=∠OFN=∠EOF=90°.
∵∠MON=90°,
∴∠EOM=∠FON,
∴△OEM≌△OFN,
∴EM=FN,
∴CM+CN=CE+CF=4,
∴OE=2,
∴☉O的面积为4π.
故选C.
15.A [解析]
作AH⊥BC于点H,如图.由题意知BE=2t,BD=8-2t.
∵AB=AC=5,∴BH=CH=BC=4.
∵直线DE与☉O相切,∴∠BED=90°.
又∵∠EBD=∠ABH,∴△BED∽△BHA,
∴=,即=,
解得t=.
16.C [解析]
如图所示,连接OC,OB,CF,BE.
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,∴=.
∵=,
∴=,故①正确.
在△BOG与△COH中,∵∠BOG=∠COH,OB=OC,∠OBG=∠OCH=45°,
∴△BOG≌△COH,∴OG=OH.
又∵∠HOG=90°,∴△OGH是等腰直角三角形,②正确.
∴S△OBG=S△OCH,
∴S四边形OGBH=S△BOC=S正方形ABCD=定值,故③错误.
∵△BGH的周长=GH+BG+BH=GH+BH+HC=GH+BC,
∴当OH⊥BC时,OH的值最小,则GH的值最小,此时OG=OH=2,GH=2,
∴△BGH的周长的最小值为4+2,故④错误.
∴①②正确,故选C.
17.相切,相离 [解析]
在Rt△ABC中,∵∠ACB=30°,∴AB=AC=4
cm,∴BC==4
cm>4
cm,∴点B到AD的距离等于半径,点B到CD的距离大于半
径,∴☉B与直线AD相切,☉B与直线CD相离.
18.4或2.56
19.(1)40° (2)8 [解析]
(1)连接OB.
∵BC是☉O的切线,
∴∠OBC=90°.
∵OP⊥OA,
∴∠AOP=90°,
∴∠APO=90°-∠A=70°,
∴∠BPC=70°.
∵OA=OB,
∴∠ABO=∠A=20°,
∴∠CBP=90°-∠OBA=70°,
∴∠BCO=180°-∠CBP-∠BPC=40°.
(2)∵∠CBA+∠ABO=90°,∠APO+∠A=90°,
又∠ABO=∠A,
∴∠CBA=∠APO=∠CPB,
∴CP=CB.
设BC=x,则PC=x.
在Rt△OBC中,OB=OA=6,OC=CP+OP=x+2.
∵OB2+BC2=OC2,
∴62+x2=(x+2)2,
解得x=8,即BC的长为8.
20.解:(1)连接OB.∵在Rt△ABC中,AB=13,AC=5,
∴BC===12.
∵☉O的半径OC=3,BC=12,
∴OB==>3,
∴点B在☉O外.
∵AC=5,OC=3,∴AO=2<3,
∴点A在☉O内.
(2)AB与☉O相切.
证明:过点O作OE⊥AB于点E,
则有Rt△AOE∽Rt△ABC,
∴=,
∴OE===2.4,
∴OE=OC,
∴AB与☉O相切.
21.解:(1)证明:∵PA,PB分别与☉O相切于点A,B,
∴PA=PB.
又∠P=60°,
∴△PAB是等边三角形.
(2)∵△PAB是等边三角形,
∴AB=PB=2
cm,∠PBA=60°.
∵BC是☉O的直径,PB是☉O的切线,
∴∠CAB=90°,∠PBC=90°,
∴∠ABC=30°,
∴tan∠ABC==,
∴AC=2×=(cm).
22.解:(1)AF与☉O相切.
理由:如图,连接
OC.
∵PC为☉O的切线,
∴∠OCP=90°.
∵AB是☉O的直径,
∴∠BCA=90°.
∵OF∥BC,∴∠AEO=∠BCA=90°,
∴OF⊥AC.
又∵OC=OA,
∴∠COF=∠AOF.
又∵OF=OF,
∴△OCF≌△OAF,
∴∠OAF=∠OCF=90°,
∴AF⊥OA.
∵点A在☉O上,
∴AF与☉O相切.
(2)∵☉O的半径为4,AF=3,AF⊥OA,
∴在Rt△OFA中,OF===5.
∵∠AEO=∠OAF=90°,∠AOE=∠FOA,
∴△AOE∽△FOA,
∴=,即=,解得AE=.
∵OF⊥AC,
∴AC=2AE=.
23.解:(1)证明:如图,连接OE.
∵AB=BC,
∴∠A=∠C.
∵OE=OC,
∴∠OEC=∠C,
∴∠A=∠OEC,∴OE∥AB.
∵AB⊥EG,∴OE⊥EG.
∵OE为☉O的半径,
∴EG是☉O的切线.
(2)∵EG⊥AB,∴∠BFG=90°.
∵GF=2,GB=4,
∴BF==2.
∵BF∥OE,∴△BGF∽△OGE,
∴=,
即=,解得OE=4,
即☉O的半径为4.
24.解:(1)连接OD.
∵AB是☉O的直径,∠BAC=38°,
∴∠ACB=90°,
∴∠ABC=90°-38°=52°.
∵D为的中点,∠AOB=180°,
∴∠BOD=90°.
∵OD=OB,∴∠ABD=∠ODB,
∴∠ABD=(180°-∠BOD)=45°.
(2)连接OD.
∵DP切☉O于点D,∴OD⊥DP,
即∠ODP=90°.
∵DP∥AC,∴∠P=∠BAC=38°.
∵∠AOD是△ODP的一个外角,
∴∠AOD=∠P+∠ODP=128°,
∴∠ACD=64°.
∵OC=OA,
∴∠OCA=∠BAC=38°,
∴∠OCD=∠ACD-∠OCA=64°-38°=26°.
25.解:(1)证明:如图,连接OC.
∵OA=OC,
∴∠OCA=∠BAC=60°.
∵AP=AC,且∠P+∠PCA=∠BAC=60°,
∴∠P=∠PCA=30°,
∴∠PCO=∠PCA+∠OCA=90°.
∵点C在☉O上,∴PC为☉O的切线.
(2)证明:如图,连接AD.
∵AB是☉O的直径,
∴∠ACB=∠ADB=90°.
又∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴AD=BD.
∵在Rt△ADB中,AD2+BD2=AB2,
∴AD=BD=AB.
∵OA=OC,∠BAC=60°,
∴△ACO为等边三角形,∴AC=OC=OA,
∴AP=AC=OA=AB,∴BD=AP.
(3)∵∠PCE=∠PCA+∠ACD=75°,∠P=30°,
∴∠PEC=75°,
∴PC=PE=6.
∵在Rt△PCO中,OP=OA+AP=2OC,OP2=PC2+OC2,
∴OC=6,OP=12,
∴OE=OP-PE=12-6,
∴AE=OA-OE=OC-OE=6-(12-6)=6-6.
26.解:(1)证明:∵∠AOB=∠COD=60°,
∴∠COA+∠AOD=∠DOB+∠AOD,
∴∠COA=∠DOB.
在△OAC和△OBD中,
∵OC=OD,∠COA=∠DOB,OA=OB,
∴△OAC≌△OBD,∴AC=BD.
(2)∵OC是半圆A的切线,
∴AC⊥OC,即∠OCA=90°.
在Rt△OCA中,由勾股定理,得OC2+AC2=OA2,
∴OC2+12=42,解得OC=(负值不合题意,已舍去).
在△COD中,∵OC=OD,∠COD=60°,
∴△COD是等边三角形,∴CD=OC=.
(3)设点C到OA的距离为h.
∵S△AOC=OA·h,OA=4,
∴当h最大时,S△AOC最大,即当C为半圆A的中点时,h最大,此时h=1,∴S△AOC的最大值=×4×1=2.
[时间:120分钟 分值:120分]
一、选择题(本大题共16个小题,共42分.1~10小题,每小题3分;11~16小题,每小题2分.在每小题给出的四个选项中,只有一项符合题目要求)
1.已知☉O的半径为3,直线l与☉O相交,则圆心O到直线l的距离d的取值范围是( )
A.d=3
B.d>3
C.0≤d<3
D.0
A.1
B.2
C.3
D.4
3.以点O为中心的量角器与三角尺ABC如图1所示摆放,直角顶点B在零刻度线所在直线DE上,且量角器与三角尺只有一个公共点P,若点P的读数为35°,则∠CBD的度数是( )
图1
A.55°
B.45°
C.35°
D.25°
4.如图2,在☉O中,AB为直径,BC为弦,CD为切线,连接OC.若∠BCD=50°,则∠AOC的度数为
( )
图2
A.40°
B.50°
C.80°
D.100°
5.已知☉O的面积为2π,则其内接正三角形的面积为
( )
A.3
B.3
C.
D.
6.如图3,☉O内切于△ABC,切点分别为D,E,F.已知∠B=50°,∠C=60°,连接DE,DF,那么∠EDF的度数为
( )
图3
A.40°
B.55°
C.65°
D.70°
7.如图4,在等腰直角三角形ABC中,AB=AC=4,O为BC的中点,以点O为圆心作半圆交BC于点M,N,与AB,AC相切,切点分别为D,E,则☉O的半径和∠MND的度数分别为( )
图4
A.2,22.5°
B.3,30°
C.3,22.5°
D.2,30°
8.《九章算术》中有一题“今有勾八步,股十五步,问勾中容圆径几何.”其意思是:如图5,今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,则该直角三角形能容纳的圆形(内切圆)直径是
( )
图5
A.6步
B.7步
C.8步
D.9步
9.如图6,已知点A,B在半径为1的☉O上,∠AOB=60°,延长OB至点C,过点C作直线OA的垂线,记为l,则下列说法正确的是
( )
图6
A.当BC等于0.5时,l与☉O相离
B.当BC等于2时,l与☉O相切
C.当BC等于1时,l与☉O相交
D.当BC不为1时,l与☉O不相切
10.如图7,已知☉O的弦AB=8,以AB为一边作正方形ABCD,CD边与☉O相切,切点为E,则☉O的半径为
( )
图7
A.10
B.8
C.6
D.5
11.如图8,一条公路环绕山脚的部分是一段圆弧形状(O为圆心),过A,B两点的切线交于点C,测得∠C=120°,A,B两点之间的距离为60
m,则这段公路的长度是
( )
图8
A.10π
m
B.20π
m
C.10π
m
D.60
m
12.如图9,在△ABC中,BC=4,☉P与△ABC的边或边的延长线相切.若☉P的半径为2,△ABC的面积为5,则△ABC的周长为( )
图9
A.8
B.10
C.13
D.14
13.如图10,四边形ABCD内接于☉O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为
( )
图10
A.56°
B.62°
C.68°
D.78°
14.如图11,☉O内切于正方形ABCD,O为圆心,作∠MON=90°,其两边分别交BC,CD于点N,M,若CM+CN=4,则☉O的面积为
( )
图11
A.π
B.2π
C.4π
D.0.5π
15.如图12,在等腰三角形ABC中,AB=AC=5
cm,BC=8
cm.动点D从点C出发,沿线段CB以2
cm/s的速度向点B运动,同时动点O从点B出发,沿线段BA以1
cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也停止运动.设运动时间为t
s,以点O为圆心,OB长为半径的☉O与BA交于另一点E,连接ED.当直线DE与☉O相切时,t的值是
( )
图12
A.
B.
C.
D.
16.如图13,边长为4的正方形ABCD内接于☉O,E是上的一动点(不与点A,B重合),F是上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°,有以下结论:
①=;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为4+.
其中正确的是( )
图13
A.①③④
B.①②③
C.①②
D.③④
二、填空题(本大题共3个小题,共12分.17,18小题,每小题3分,19小题共6分,把答案写在题中横线上)
17.
在矩形ABCD中,AC=8
cm,∠ACB=30°,以点B为圆心,4
cm长为半径作☉B,则☉B与直线AD和CD的位置关系依次是 .?
18.如图14,AB为☉O的直径,C为☉O上一点,过点B的切线交AC的延长线于点D,E为弦AC的中点,AD=10,BD=6.若P为直径AB上的一个动点,连接EP,当△AEP是直角三角形时,AP的长为 .?
图14
19.如图15,AB是☉O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且BC是☉O的切线.
(1)若∠A=20°,则∠BCO= ;?
(2)若OA=6,OP=2,则BC的长是 .?
图15
三、解答题(本大题共7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8分)如图16,已知在Rt△ABC中,∠C=90°,AB=13,AC=5,O是AC边上的点,以点O为圆心,OC为半径作☉O.
(1)当OC=3时,判断点A、点B与☉O的位置关系;
(2)当OC=2.4时,AB与☉O有怎样的位置关系?请证明你的结论.
图16
21.(本小题满分9分)如图17,PA,PB分别与☉O相切于点A,B,AC为弦,BC为☉O的直径,若∠P=60°,PB=2
cm.
(1)求证:△PAB是等边三角形;
(2)求AC的长.
图17
22.(本小题满分9分)如图18,△ABC内接于☉O,AB是☉O的直径,☉O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.
(1)判断AF与☉O的位置关系,并说明理由;
(2)若☉O的半径为4,AF=3,求AC的长.
图18
23.(本小题满分9分)如图19,AB=BC,以BC为直径作☉O,AC交☉O于点E,过点E作EG⊥AB于点F,交CB的延长线于点G.
(1)求证:EG是☉O的切线;
(2)若GF=2,GB=4,求☉O的半径.
图19
24.(本小题满分10分)已知AB是☉O的直径,弦CD与AB相交,∠BAC=38°.
(1)如图20①,若D为的中点,求∠ABC和∠ABD的大小;
(2)如图②,过点D作☉O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
图20
25.(本小题满分10分)如图21,△ABC内接于☉O,AB为直径,∠BAC=60°,延长BA至点P,使AP=AC,作CD平分∠ACB交AB于点E,交☉O于点D,连接PC,BD.
(1)求证:PC为☉O的切线;
(2)求证:BD=AP;
(3)若PC=6,求AE的长.
图21
26.(本小题满分11分)已知OA=OB=4,∠AOB=60°,半圆A的半径为1,点C是半圆上任意一点,连接OC,把OC绕点O顺时针旋转60°到OD的位置,连接BD.
(1)如图22①,求证:AC=BD;
(2)如图22②,当OC与半圆A相切于点C时,求CD的长;
(3)直接写出△AOC面积的最大值.
图22
参考答案
1.C
2.B [解析]
如图所示,∵四边形ABCD是菱形,AC=6,
∴AC⊥BD,AO=CO=AC=3,BO=DO.
∵AB=4,
∴DO=BO===.
∵r=3=AO=CO,BO=DO=<3,
∴A,B,C,D四个点中在☉O上的个数为2.
3.C [解析]
∵AB是☉O的切线,∴∠OPB=90°.又∵∠ABC=90°,∴OP∥BC,
∴∠CBD=∠POB=35°.
4.C [解析]
∵在☉O中,CD为切线,
∴∠OCD=90°.
∵∠BCD=50°,∴∠OCB=40°.
∵OC=OB,∴∠OBC=∠OCB=40°,
∴∠AOC=80°.
5.C [解析]
由☉O的面积为2π,可求得☉O的半径为.如图,△ABC为正三角形,OC=,∠OCD=30°,过点O作OD⊥BC于点D.由cos30°=得CD=,
∴BC=,
∴S△ABC=BC2=.
6.B [解析]
如图,连接OE,OF.∵∠A+∠B+∠C=180°,∠B=50°,∠C=60°,∴∠A=70°.
∵☉O内切于△ABC,
切点分别为D,E,F,∴∠OEA=∠OFA=90°,
∴∠EOF=360°-∠A-∠OEA-∠OFA=110°,∴∠EDF=∠EOF=55°.
7.A [解析]
∵AB为☉O的切线,
∴OD⊥AB,∴∠ODB=∠A=90°.
又∠B=∠B,∴△OBD∽△CBA,
∴==,∠DOB=∠C=45°,
∴OD=CA=2,∠MND=∠DOB=22.5°.
故选A.
8.A [解析]
根据勾股定理得,斜边长为=17(步),则该直角三角形能容纳的圆形(内切圆)半径r==3(步),则直径为6步,故选A.
9.D [解析]
设直线l与OA的垂足为D.
A项,∵BC=0.5,∴OC=OB+BC=1.5.
∵∠AOB=60°,
∴∠C=30°,∴DO=OC=0.75<1,
∴l与☉O相交,故A项错误;
B项,∵BC=2,∴OC=OB+BC=3.
∵∠AOB=60°,
∴∠C=30°,∴DO=OC=1.5>1,
∴l与☉O相离,故B项错误;
C项,∵BC=1,∴OC=OB+BC=2.
∵∠AOB=60°,∴∠C=30°,∴DO=OC=1,
∴l与☉O相切,故C项错误;
D项,∵BC≠1,
∴OC=OB+BC≠2.
∵∠AOB=60°,∴∠C=30°,
∴DO=OC≠1,
∴l与☉O不相切,故D项正确.故选D.
10.D [解析]
连接EO并延长交AB于点F,连接OA.
∵CD边与☉O相切,∴OE⊥CD.
∵四边形ABCD是正方形,
∴AB∥CD,AD=AB=8,
∴EF⊥AB,
∴四边形AFED是矩形,AF=AB=4,
∴EF=AD=8.
∵OA=OE,∴OF=8-OA.
∵OA2=AF2+OF2,∴OA2=42+(8-OA)2,
解得OA=5,∴☉O的半径为5.
11.B [解析]
∵AC与BC是☉O的切线,∠C=120°,
∴∠OAC=∠OBC=90°,AC=BC,
∴∠AOB=60°.
又∵OA=OB,∴△AOB是等边三角形,
∴OA=AB=60
m.
∴公路的长度==20π(m).
12.C [解析]
如图,设切点分别为E,F,G,连接PE,PF,PG,AP.
由题意可知∠PEC=∠PFA=∠PGA=90°,
∴S△PBC=BC·PE=×4×2=4,
由切线长定理可知S△PFC+S△PBG=S△PBC=4,
∴S四边形AFPG=S△ABC+S△PFC+S△PBG+S△PBC=5+4+4=13.
由切线长定理可知S△APG=S四边形AFPG=,
∴=AG·PG,∴AG=.
由切线长定理可知CE=CF,BE=BG,
∴△ABC的周长为AC+AB+CE+BE=AC+AB+CF+BG=AF+AG=2AG=13.
13.C [解析]
∵点I是△ABC的内心,
∴∠BAC=2∠IAC,∠ACB=2∠ICA.
∵∠AIC=124°,
∴∠B=180°-(∠BAC+∠ACB)=180°-2(∠IAC+∠ICA)=180°-2(180°-∠AIC)=68°.
∵四边形ABCD内接于☉O,
∴∠CDA=180°-∠B=112°,
∴∠CDE=180°-∠CDA=68°.
14.C [解析]
如图,设☉O与正方形ABCD的边CD切于点E,与BC切于点F,连接OE,OF,
则四边形OECF是正方形,
∴CF=CE=OE=OF,∠OEM=∠OFN=∠EOF=90°.
∵∠MON=90°,
∴∠EOM=∠FON,
∴△OEM≌△OFN,
∴EM=FN,
∴CM+CN=CE+CF=4,
∴OE=2,
∴☉O的面积为4π.
故选C.
15.A [解析]
作AH⊥BC于点H,如图.由题意知BE=2t,BD=8-2t.
∵AB=AC=5,∴BH=CH=BC=4.
∵直线DE与☉O相切,∴∠BED=90°.
又∵∠EBD=∠ABH,∴△BED∽△BHA,
∴=,即=,
解得t=.
16.C [解析]
如图所示,连接OC,OB,CF,BE.
∵∠BOE+∠BOF=90°,∠COF+∠BOF=90°,
∴∠BOE=∠COF,∴=.
∵=,
∴=,故①正确.
在△BOG与△COH中,∵∠BOG=∠COH,OB=OC,∠OBG=∠OCH=45°,
∴△BOG≌△COH,∴OG=OH.
又∵∠HOG=90°,∴△OGH是等腰直角三角形,②正确.
∴S△OBG=S△OCH,
∴S四边形OGBH=S△BOC=S正方形ABCD=定值,故③错误.
∵△BGH的周长=GH+BG+BH=GH+BH+HC=GH+BC,
∴当OH⊥BC时,OH的值最小,则GH的值最小,此时OG=OH=2,GH=2,
∴△BGH的周长的最小值为4+2,故④错误.
∴①②正确,故选C.
17.相切,相离 [解析]
在Rt△ABC中,∵∠ACB=30°,∴AB=AC=4
cm,∴BC==4
cm>4
cm,∴点B到AD的距离等于半径,点B到CD的距离大于半
径,∴☉B与直线AD相切,☉B与直线CD相离.
18.4或2.56
19.(1)40° (2)8 [解析]
(1)连接OB.
∵BC是☉O的切线,
∴∠OBC=90°.
∵OP⊥OA,
∴∠AOP=90°,
∴∠APO=90°-∠A=70°,
∴∠BPC=70°.
∵OA=OB,
∴∠ABO=∠A=20°,
∴∠CBP=90°-∠OBA=70°,
∴∠BCO=180°-∠CBP-∠BPC=40°.
(2)∵∠CBA+∠ABO=90°,∠APO+∠A=90°,
又∠ABO=∠A,
∴∠CBA=∠APO=∠CPB,
∴CP=CB.
设BC=x,则PC=x.
在Rt△OBC中,OB=OA=6,OC=CP+OP=x+2.
∵OB2+BC2=OC2,
∴62+x2=(x+2)2,
解得x=8,即BC的长为8.
20.解:(1)连接OB.∵在Rt△ABC中,AB=13,AC=5,
∴BC===12.
∵☉O的半径OC=3,BC=12,
∴OB==>3,
∴点B在☉O外.
∵AC=5,OC=3,∴AO=2<3,
∴点A在☉O内.
(2)AB与☉O相切.
证明:过点O作OE⊥AB于点E,
则有Rt△AOE∽Rt△ABC,
∴=,
∴OE===2.4,
∴OE=OC,
∴AB与☉O相切.
21.解:(1)证明:∵PA,PB分别与☉O相切于点A,B,
∴PA=PB.
又∠P=60°,
∴△PAB是等边三角形.
(2)∵△PAB是等边三角形,
∴AB=PB=2
cm,∠PBA=60°.
∵BC是☉O的直径,PB是☉O的切线,
∴∠CAB=90°,∠PBC=90°,
∴∠ABC=30°,
∴tan∠ABC==,
∴AC=2×=(cm).
22.解:(1)AF与☉O相切.
理由:如图,连接
OC.
∵PC为☉O的切线,
∴∠OCP=90°.
∵AB是☉O的直径,
∴∠BCA=90°.
∵OF∥BC,∴∠AEO=∠BCA=90°,
∴OF⊥AC.
又∵OC=OA,
∴∠COF=∠AOF.
又∵OF=OF,
∴△OCF≌△OAF,
∴∠OAF=∠OCF=90°,
∴AF⊥OA.
∵点A在☉O上,
∴AF与☉O相切.
(2)∵☉O的半径为4,AF=3,AF⊥OA,
∴在Rt△OFA中,OF===5.
∵∠AEO=∠OAF=90°,∠AOE=∠FOA,
∴△AOE∽△FOA,
∴=,即=,解得AE=.
∵OF⊥AC,
∴AC=2AE=.
23.解:(1)证明:如图,连接OE.
∵AB=BC,
∴∠A=∠C.
∵OE=OC,
∴∠OEC=∠C,
∴∠A=∠OEC,∴OE∥AB.
∵AB⊥EG,∴OE⊥EG.
∵OE为☉O的半径,
∴EG是☉O的切线.
(2)∵EG⊥AB,∴∠BFG=90°.
∵GF=2,GB=4,
∴BF==2.
∵BF∥OE,∴△BGF∽△OGE,
∴=,
即=,解得OE=4,
即☉O的半径为4.
24.解:(1)连接OD.
∵AB是☉O的直径,∠BAC=38°,
∴∠ACB=90°,
∴∠ABC=90°-38°=52°.
∵D为的中点,∠AOB=180°,
∴∠BOD=90°.
∵OD=OB,∴∠ABD=∠ODB,
∴∠ABD=(180°-∠BOD)=45°.
(2)连接OD.
∵DP切☉O于点D,∴OD⊥DP,
即∠ODP=90°.
∵DP∥AC,∴∠P=∠BAC=38°.
∵∠AOD是△ODP的一个外角,
∴∠AOD=∠P+∠ODP=128°,
∴∠ACD=64°.
∵OC=OA,
∴∠OCA=∠BAC=38°,
∴∠OCD=∠ACD-∠OCA=64°-38°=26°.
25.解:(1)证明:如图,连接OC.
∵OA=OC,
∴∠OCA=∠BAC=60°.
∵AP=AC,且∠P+∠PCA=∠BAC=60°,
∴∠P=∠PCA=30°,
∴∠PCO=∠PCA+∠OCA=90°.
∵点C在☉O上,∴PC为☉O的切线.
(2)证明:如图,连接AD.
∵AB是☉O的直径,
∴∠ACB=∠ADB=90°.
又∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴AD=BD.
∵在Rt△ADB中,AD2+BD2=AB2,
∴AD=BD=AB.
∵OA=OC,∠BAC=60°,
∴△ACO为等边三角形,∴AC=OC=OA,
∴AP=AC=OA=AB,∴BD=AP.
(3)∵∠PCE=∠PCA+∠ACD=75°,∠P=30°,
∴∠PEC=75°,
∴PC=PE=6.
∵在Rt△PCO中,OP=OA+AP=2OC,OP2=PC2+OC2,
∴OC=6,OP=12,
∴OE=OP-PE=12-6,
∴AE=OA-OE=OC-OE=6-(12-6)=6-6.
26.解:(1)证明:∵∠AOB=∠COD=60°,
∴∠COA+∠AOD=∠DOB+∠AOD,
∴∠COA=∠DOB.
在△OAC和△OBD中,
∵OC=OD,∠COA=∠DOB,OA=OB,
∴△OAC≌△OBD,∴AC=BD.
(2)∵OC是半圆A的切线,
∴AC⊥OC,即∠OCA=90°.
在Rt△OCA中,由勾股定理,得OC2+AC2=OA2,
∴OC2+12=42,解得OC=(负值不合题意,已舍去).
在△COD中,∵OC=OD,∠COD=60°,
∴△COD是等边三角形,∴CD=OC=.
(3)设点C到OA的距离为h.
∵S△AOC=OA·h,OA=4,
∴当h最大时,S△AOC最大,即当C为半圆A的中点时,h最大,此时h=1,∴S△AOC的最大值=×4×1=2.
