冀教版九年级数学下册第三十二章投影与视图巩固检测题(word版含答案)
文档属性
| 名称 | 冀教版九年级数学下册第三十二章投影与视图巩固检测题(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 472.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览



文档简介
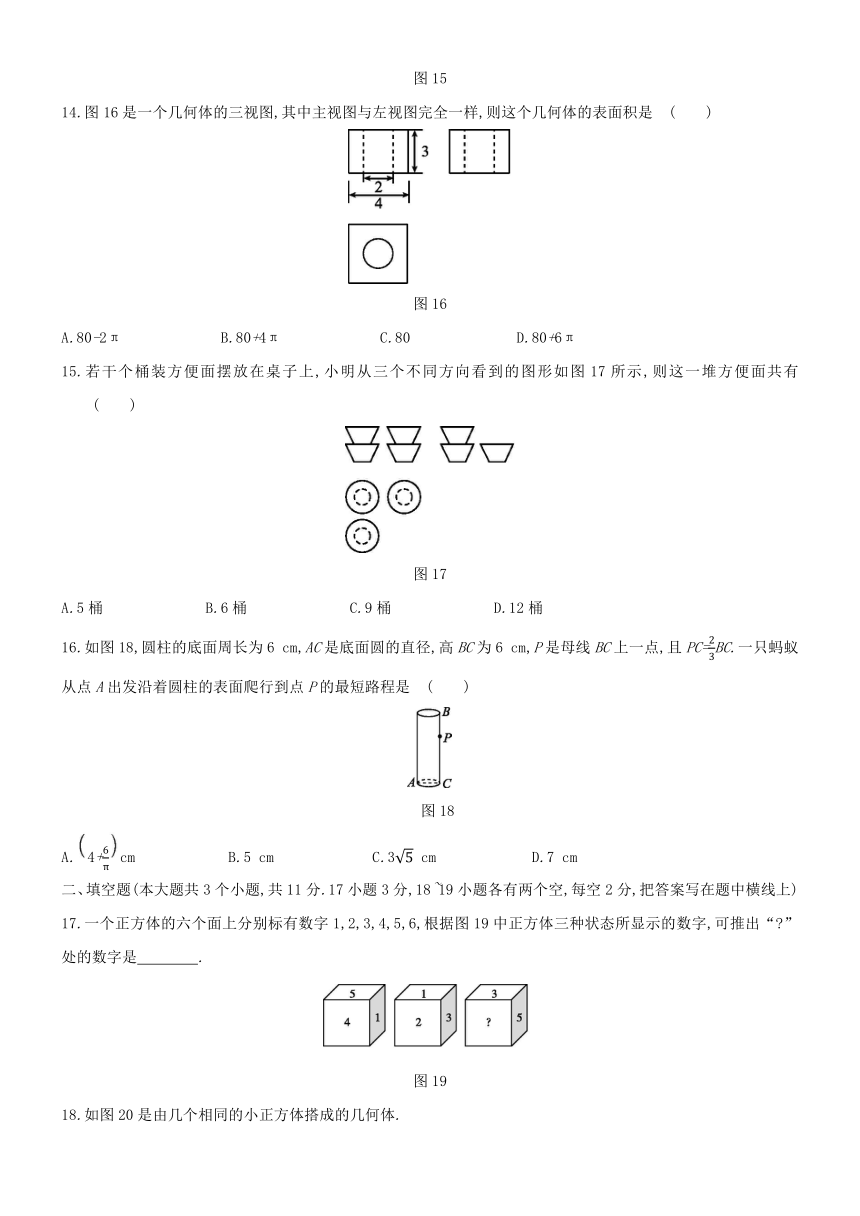
冀教版九年级数学下第三十二章投影与视图巩固检测题
[时间:120分钟 分值:120分]
一、选择题(本大题共16个小题,共42分.1~10小题,每小题3分;11~16小题,每小题2分.在每小题给出的四个选项中,只有一项符合题目要求)
1.下列哪种影子不是中心投影
( )
A.太阳光下林荫道上的树影
B.晚上在房间内墙上的手影
C.舞厅中霓虹灯形成的影子
D.皮影戏中的影子
2.下列图形中,可能表示同一地点的两棵小树在同一时刻阳光下的影子的是
( )
图1
3.下列各图中,是一个正方体的表面展开图的是
( )
图2
4.一个由半球和圆柱组成的几何体如图3水平放置,则其俯视图为
( )
图3
图4
5.把一个正五棱柱如图5摆放,当投射光线由正前方射到后方时,它的正投影大致是( )
图5
图6
6.如图7是一个用于防震的L形的包装用泡沫塑料,则它的左视图是
( )
图7
图8
7.在图9上剪去①②③④中的一个图形,剩下的图形可以折叠成一个长方体,则剪去的这个图形是
( )
图9
A.①
B.②
C.③
D.④
8.如图10,夜晚路灯下有一排同样高的旗杆,离路灯越近,旗杆的影子
( )
图10
A.越长
B.越短
C.一样长
D.随时间变化而变化
9.如图11是由5个完全相同的小正方体搭成的几何体,如果将小正方体A放到小正方体B的正上方,则该几何体的
( )
图11
A.主视图会发生改变
B.俯视图会发生改变
C.左视图会发生改变
D.三种视图都会发生改变
10.某几何体的三视图如图12所示,则下列说法错误的是
( )
图12
A.该几何体是长方体
B.该几何体的高是3
C.底面有一边的长是1
D.该几何体的表面积为18平方单位
11.对于一个圆柱的三种视图,小明同学求出其中两种视图的面积分别为6和10,则该圆柱第三种视图的面积为
( )
A.6
B.10
C.4
D.6或10
12.如图13,正方体的表面展开图中,对面数字之和相等,则-xy=
( )
图13
A.9
B.-9
C.-6
D.-8
13.如图14,一个几何体上半部分为正四棱锥,下半部分为立方体,且有一个面涂有颜色,则该几何体的表面展开图可能是
( )
图14
图15
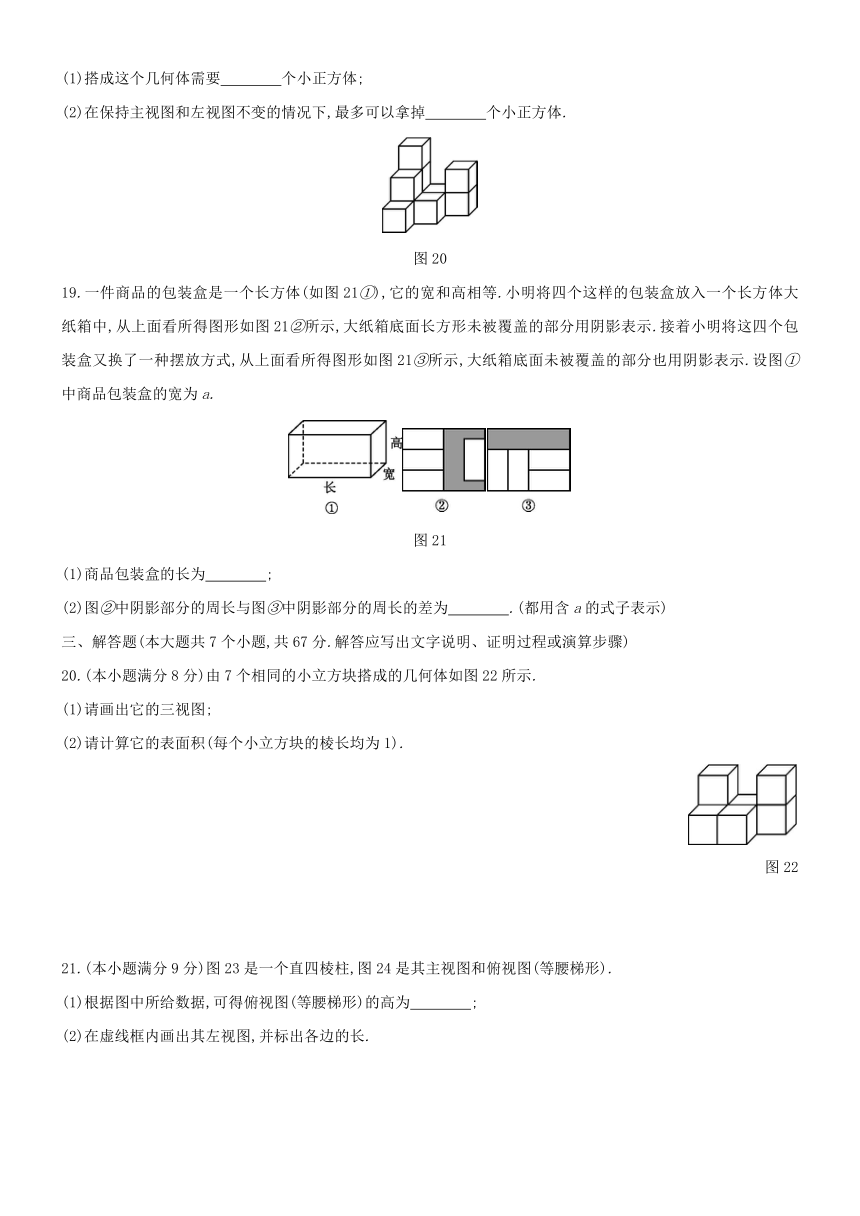
14.图16是一个几何体的三视图,其中主视图与左视图完全一样,则这个几何体的表面积是
( )
图16
A.80-2π
B.80+4π
C.80
D.80+6π
15.若干个桶装方便面摆放在桌子上,小明从三个不同方向看到的图形如图17所示,则这一堆方便面共有
( )
图17
A.5桶
B.6桶
C.9桶
D.12桶
16.如图18,圆柱的底面周长为6
cm,AC是底面圆的直径,高BC为6
cm,P是母线BC上一点,且PC=BC.一只蚂蚁从点A出发沿着圆柱的表面爬行到点P的最短路程是
( )
图18
A.4+cm
B.5
cm
C.3
cm
D.7
cm
二、填空题(本大题共3个小题,共11分.17小题3分,18~19小题各有两个空,每空2分,把答案写在题中横线上)
17.一个正方体的六个面上分别标有数字1,2,3,4,5,6,根据图19中正方体三种状态所显示的数字,可推出“?”处的数字是 .?
图19
18.如图20是由几个相同的小正方体搭成的几何体.
(1)搭成这个几何体需要 个小正方体;?
(2)在保持主视图和左视图不变的情况下,最多可以拿掉 个小正方体.?
图20
19.一件商品的包装盒是一个长方体(如图21①),它的宽和高相等.小明将四个这样的包装盒放入一个长方体大纸箱中,从上面看所得图形如图21②所示,大纸箱底面长方形未被覆盖的部分用阴影表示.接着小明将这四个包装盒又换了一种摆放方式,从上面看所得图形如图21③所示,大纸箱底面未被覆盖的部分也用阴影表示.设图①中商品包装盒的宽为a.
图21
(1)商品包装盒的长为 ;?
(2)图②中阴影部分的周长与图③中阴影部分的周长的差为 .(都用含a的式子表示)?
三、解答题(本大题共7个小题,共67分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8分)由7个相同的小立方块搭成的几何体如图22所示.
(1)请画出它的三视图;
(2)请计算它的表面积(每个小立方块的棱长均为1).
图22
21.(本小题满分9分)图23是一个直四棱柱,图24是其主视图和俯视图(等腰梯形).
(1)根据图中所给数据,可得俯视图(等腰梯形)的高为 ;?
(2)在虚线框内画出其左视图,并标出各边的长.
图23
图24
22.(本小题满分9分)小红想利用太阳光下的影长测量学校旗杆AB的高度.如图25,她在某一时刻在地面上竖立一个2米长的标杆CD,测得其影长DE=0.4米.
(1)请在图中画出此时旗杆AB在太阳光下的投影BF;
(2)如果BF=1.6米,求旗杆AB的高.
图25
23.(本小题满分9分)在一个长方体的各个面上分别标有字母A,B,C,D,E,F,将这个长方体如图26所示展开.
(1)如果A面在长方体的底部,那么 面会在上面;?
(2)求这个长方体的表面积和体积.
图26
24.(本小题满分10分)如图27所示,甲物体高4米,影长3米,乙物体高2米,影长4米,两物体相距5米.
(1)在图中画出灯的位置,并画出丙物体的影子;
(2)若灯杆、甲、乙都与地面垂直并且底部在同一直线上,试求出灯的高度.
图27
25.(本小题满分10分)如图28所示,在一面与地面垂直的墙面的同一侧有一根高10米的旗杆AB和一个高度未知的电线杆CD.它们都与地面垂直.为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光的照射下,旗杆落在墙面上的影子EF的长度为2米,落在地面上的影子BF的长度为10米;而电线杆落在墙面上的影子GH的长度为3米,落在地面上的影子DH的长度为5米.依据这些数据,该小组的同学计算出了电线杆的高度.
(1)该小组的同学在这里利用的是 投影的有关知识进行计算的;?
(2)试计算出电线杆的高度,并写出计算过程.
图28
26.(本小题满分12分)如图29①,一个无盖的正方体盒子的棱长为10厘米,顶点C1处有一只昆虫甲,在盒子的内部顶点A处有一只昆虫乙.(盒壁的厚度忽略不计)
(1)假设昆虫甲在顶点C1处静止不动,在图①中画出一条路径,使昆虫乙从顶点A沿这条路径爬行,可以在最短的时间内捕捉到昆虫甲(请简要说明画法);
(2)如图29②,假设昆虫甲静止不动,昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,那么昆虫乙至少需要爬行多长时间才能捕捉到昆虫甲?
(3)如图29②,假设昆虫甲从顶点C1以1厘米/秒的速度在盒子的内部沿棱C1C向下爬行,同时昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,那么昆虫乙至少需要爬行多长时间才能捕捉到昆虫甲?(精确到1秒,参考数据:≈4.4,≈4.6)
图29
参考答案
1.A [解析]
∵晚上在房间内墙上的手影、舞厅中霓虹灯形成的影子、皮影戏中的影子,它们的光源都是灯光,故它们都是中心投影,太阳光下林荫道上的树影的光源是太阳光,这是平行投影,故选A.
2.A [解析]
A项,影子的方向相同,且较高的树的影子长度大于较低的树的影子,故本选项符合题意;B项,影子的方向不相同,故本选项不符合题意;C项,影子的方向不相同,故本选项不符合题意;D项,树高与影子长度不成正比,故本选项不符合题意.故选A.
3.C
4.A
5.B
6.A [解析]
从左面看可得到一个带有虚线的矩形.
7.A
8.B [解析]
如图,由图易得AB9.A [解析]
如果将小正方体A放到小正方体B的正上方,则它的主视图会发生改变,俯视图和左视图不变.
故选A.
10.D [解析]
A.该几何体是长方体,正确;B.该几何体的高为3,正确;C.底面有一边的长是1,正确;D.该几何体的表面积为2×(1×2+2×3+1×3)=22(平方单位),错误.故选D.
11.D [解析]
∵圆柱的三种视图分别是矩形、矩形、圆,视图为矩形的两种视图的面积相等,且小明同学求出其中两种视图的面积分别为6和10,∴该圆柱第三种视图的面积为6或10.
12.B [解析]
∵1与6相对,4与x相对,5与y相对,∴1+6=4+x=5+y,∴x=3,y=2,
∴-xy=-32=-9.
13.B [解析]
选项A和C涂有颜色的面是底面,不能折叠成原几何体的形式;选项B能折叠成原几何体的形式;选项D中的图形不是这个几何体的表面展开图.故选B.
14.B [解析]
由三视图可知,该几何体是长方体,中间是空心圆柱,长方体的长、宽、高分别为4,4,3,圆柱底面圆直径为2,高为3,则长方体的表面积为4×4×2+4×3×4=80,圆柱的侧面积为2π×3=6π,上、下表面空心圆的面积和为2π,∴这个几何体的表面积是80+6π-2π=80+4π.
15.A [解析]
如图,2+2+1=5,故选A.
16.B [解析]首先画出圆柱的侧面展开图,根据高BC=6
cm,PC=BC,求出PC=×6=4(cm).在Rt△ACP中,根据勾股定理求出AP的长即可.具体的解答过程如下:
侧面展开图如图所示,
∵圆柱的底面周长为6
cm,
∴AC=3
cm.
∵PC=BC,
∴PC=×6=4(cm).
在Rt△ACP中,AP2=AC2+PC2,
∴AP==5(cm).
故选B.
17.6 [解析]
实际动手折一个正方体,将数字标上即可得解.
18.(1)10 (2)1 [解析]
(1)这个几何体由10个小正方体组成;(2)最多可以拿掉1个小正方体.
19.(1)2a (2)2a [解析]
(1)根据摆放情况可得,包装盒的一个长等于两个宽,即长为2a;(2)包装盒的长为2a,大纸箱的长为4a,宽为3a,图②中阴影部分的周长为3a×2+2a×2+2a=12a,图③中阴影部分的周长为4a×2+2a=10a,图②中阴影部分的周长与图③中阴影部分的周长的差为12a-10a=2a.
20.解:(1)如图所示:
(2)表面积为(5+5+3)×2+2=26+2=28.
21.解:(1)4
(2)如图所示:
22.解:(1)如图所示,连接CE,过点A作AF∥CE交BD于点F,则BF即为所求.
(2)∵AF∥CE,
∴∠AFB=∠CED.
又∵∠ABF=∠CDE=90°,
∴△ABF∽△CDE,
∴=,即=,
解得AB=8(米).
答:旗杆AB的高为8
米.
23.解:(1)F [解析]
A面与F面是对面,所以如果A面在长方体的底部,那么F面会在上面.
(2)这个长方体的表面积是2×(1×3+1×2+2×3)=22(米2);
这个长方体的体积是1×2×3=6(米3).
24.解:(1)如图,点O为灯的位置,QF为丙物体的影子.
(2)如图,作OM⊥QH于点M,设OM=x米,BM=y米.
由△GAB∽△GOM,得=,即=.①
由△CDH∽△OMH,得=,即=.②
由①-②×2,得=,解得y=0.6.
把y=0.6代入①,得x=4.8.
经检验,x=4.8,y=0.6是方程①②的解.
答:灯的高度为4.8米.
25.解:(1)平行
(2)如图,分别过点E,G作EM⊥AB,GN⊥CD,垂足分别是M,N,
则有△AEM∽△CGN,MB=EF=2米,ME=BF=10米,ND=GH=3米,
NG=DH=5米,∴AM=AB-MB=10-2=8(米),CN=CD-ND=(CD-3)米.
∵△CGN∽△AEM,∴=,即=,解得CD=7(米),即电线杆的高度是7米.
26.解:(1)画出图①中A—E1—C1,A—E2—C1,A—E3—C1,A—E4—C1中任意一条路径均可(E1,E2,E3,E4分别为各棱的中点).
(2)如图②,昆虫乙爬行的最短路程为AC1==10(cm),故昆虫乙至少需要爬行10÷2=5(秒).
(3)由(1)可知,当昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙可以沿下列四种路径中的任意一种爬行:
可以看出,图③与图④中的路径相等,图⑤与图⑥中的路径相等.
设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E1→F爬行捕捉到昆虫甲需x秒.如图③,在Rt△ACF中,(2x)2=(10-x)2+202,解得x=10(负值已舍去);
设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E2→F爬行捕捉到昆虫甲需y秒.如图⑤,在Rt△ADF中,(2y)2=(20-y)2+102,解得y≈8(负值已舍去).
综上,昆虫乙至少需要爬行约8秒才能捕捉到昆虫甲.
[时间:120分钟 分值:120分]
一、选择题(本大题共16个小题,共42分.1~10小题,每小题3分;11~16小题,每小题2分.在每小题给出的四个选项中,只有一项符合题目要求)
1.下列哪种影子不是中心投影
( )
A.太阳光下林荫道上的树影
B.晚上在房间内墙上的手影
C.舞厅中霓虹灯形成的影子
D.皮影戏中的影子
2.下列图形中,可能表示同一地点的两棵小树在同一时刻阳光下的影子的是
( )
图1
3.下列各图中,是一个正方体的表面展开图的是
( )
图2
4.一个由半球和圆柱组成的几何体如图3水平放置,则其俯视图为
( )
图3
图4
5.把一个正五棱柱如图5摆放,当投射光线由正前方射到后方时,它的正投影大致是( )
图5
图6
6.如图7是一个用于防震的L形的包装用泡沫塑料,则它的左视图是
( )
图7
图8
7.在图9上剪去①②③④中的一个图形,剩下的图形可以折叠成一个长方体,则剪去的这个图形是
( )
图9
A.①
B.②
C.③
D.④
8.如图10,夜晚路灯下有一排同样高的旗杆,离路灯越近,旗杆的影子
( )
图10
A.越长
B.越短
C.一样长
D.随时间变化而变化
9.如图11是由5个完全相同的小正方体搭成的几何体,如果将小正方体A放到小正方体B的正上方,则该几何体的
( )
图11
A.主视图会发生改变
B.俯视图会发生改变
C.左视图会发生改变
D.三种视图都会发生改变
10.某几何体的三视图如图12所示,则下列说法错误的是
( )
图12
A.该几何体是长方体
B.该几何体的高是3
C.底面有一边的长是1
D.该几何体的表面积为18平方单位
11.对于一个圆柱的三种视图,小明同学求出其中两种视图的面积分别为6和10,则该圆柱第三种视图的面积为
( )
A.6
B.10
C.4
D.6或10
12.如图13,正方体的表面展开图中,对面数字之和相等,则-xy=
( )
图13
A.9
B.-9
C.-6
D.-8
13.如图14,一个几何体上半部分为正四棱锥,下半部分为立方体,且有一个面涂有颜色,则该几何体的表面展开图可能是
( )
图14
图15
14.图16是一个几何体的三视图,其中主视图与左视图完全一样,则这个几何体的表面积是
( )
图16
A.80-2π
B.80+4π
C.80
D.80+6π
15.若干个桶装方便面摆放在桌子上,小明从三个不同方向看到的图形如图17所示,则这一堆方便面共有
( )
图17
A.5桶
B.6桶
C.9桶
D.12桶
16.如图18,圆柱的底面周长为6
cm,AC是底面圆的直径,高BC为6
cm,P是母线BC上一点,且PC=BC.一只蚂蚁从点A出发沿着圆柱的表面爬行到点P的最短路程是
( )
图18
A.4+cm
B.5
cm
C.3
cm
D.7
cm
二、填空题(本大题共3个小题,共11分.17小题3分,18~19小题各有两个空,每空2分,把答案写在题中横线上)
17.一个正方体的六个面上分别标有数字1,2,3,4,5,6,根据图19中正方体三种状态所显示的数字,可推出“?”处的数字是 .?
图19
18.如图20是由几个相同的小正方体搭成的几何体.
(1)搭成这个几何体需要 个小正方体;?
(2)在保持主视图和左视图不变的情况下,最多可以拿掉 个小正方体.?
图20
19.一件商品的包装盒是一个长方体(如图21①),它的宽和高相等.小明将四个这样的包装盒放入一个长方体大纸箱中,从上面看所得图形如图21②所示,大纸箱底面长方形未被覆盖的部分用阴影表示.接着小明将这四个包装盒又换了一种摆放方式,从上面看所得图形如图21③所示,大纸箱底面未被覆盖的部分也用阴影表示.设图①中商品包装盒的宽为a.
图21
(1)商品包装盒的长为 ;?
(2)图②中阴影部分的周长与图③中阴影部分的周长的差为 .(都用含a的式子表示)?
三、解答题(本大题共7个小题,共67分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8分)由7个相同的小立方块搭成的几何体如图22所示.
(1)请画出它的三视图;
(2)请计算它的表面积(每个小立方块的棱长均为1).
图22
21.(本小题满分9分)图23是一个直四棱柱,图24是其主视图和俯视图(等腰梯形).
(1)根据图中所给数据,可得俯视图(等腰梯形)的高为 ;?
(2)在虚线框内画出其左视图,并标出各边的长.
图23
图24
22.(本小题满分9分)小红想利用太阳光下的影长测量学校旗杆AB的高度.如图25,她在某一时刻在地面上竖立一个2米长的标杆CD,测得其影长DE=0.4米.
(1)请在图中画出此时旗杆AB在太阳光下的投影BF;
(2)如果BF=1.6米,求旗杆AB的高.
图25
23.(本小题满分9分)在一个长方体的各个面上分别标有字母A,B,C,D,E,F,将这个长方体如图26所示展开.
(1)如果A面在长方体的底部,那么 面会在上面;?
(2)求这个长方体的表面积和体积.
图26
24.(本小题满分10分)如图27所示,甲物体高4米,影长3米,乙物体高2米,影长4米,两物体相距5米.
(1)在图中画出灯的位置,并画出丙物体的影子;
(2)若灯杆、甲、乙都与地面垂直并且底部在同一直线上,试求出灯的高度.
图27
25.(本小题满分10分)如图28所示,在一面与地面垂直的墙面的同一侧有一根高10米的旗杆AB和一个高度未知的电线杆CD.它们都与地面垂直.为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光的照射下,旗杆落在墙面上的影子EF的长度为2米,落在地面上的影子BF的长度为10米;而电线杆落在墙面上的影子GH的长度为3米,落在地面上的影子DH的长度为5米.依据这些数据,该小组的同学计算出了电线杆的高度.
(1)该小组的同学在这里利用的是 投影的有关知识进行计算的;?
(2)试计算出电线杆的高度,并写出计算过程.
图28
26.(本小题满分12分)如图29①,一个无盖的正方体盒子的棱长为10厘米,顶点C1处有一只昆虫甲,在盒子的内部顶点A处有一只昆虫乙.(盒壁的厚度忽略不计)
(1)假设昆虫甲在顶点C1处静止不动,在图①中画出一条路径,使昆虫乙从顶点A沿这条路径爬行,可以在最短的时间内捕捉到昆虫甲(请简要说明画法);
(2)如图29②,假设昆虫甲静止不动,昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,那么昆虫乙至少需要爬行多长时间才能捕捉到昆虫甲?
(3)如图29②,假设昆虫甲从顶点C1以1厘米/秒的速度在盒子的内部沿棱C1C向下爬行,同时昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行,那么昆虫乙至少需要爬行多长时间才能捕捉到昆虫甲?(精确到1秒,参考数据:≈4.4,≈4.6)
图29
参考答案
1.A [解析]
∵晚上在房间内墙上的手影、舞厅中霓虹灯形成的影子、皮影戏中的影子,它们的光源都是灯光,故它们都是中心投影,太阳光下林荫道上的树影的光源是太阳光,这是平行投影,故选A.
2.A [解析]
A项,影子的方向相同,且较高的树的影子长度大于较低的树的影子,故本选项符合题意;B项,影子的方向不相同,故本选项不符合题意;C项,影子的方向不相同,故本选项不符合题意;D项,树高与影子长度不成正比,故本选项不符合题意.故选A.
3.C
4.A
5.B
6.A [解析]
从左面看可得到一个带有虚线的矩形.
7.A
8.B [解析]
如图,由图易得AB
如果将小正方体A放到小正方体B的正上方,则它的主视图会发生改变,俯视图和左视图不变.
故选A.
10.D [解析]
A.该几何体是长方体,正确;B.该几何体的高为3,正确;C.底面有一边的长是1,正确;D.该几何体的表面积为2×(1×2+2×3+1×3)=22(平方单位),错误.故选D.
11.D [解析]
∵圆柱的三种视图分别是矩形、矩形、圆,视图为矩形的两种视图的面积相等,且小明同学求出其中两种视图的面积分别为6和10,∴该圆柱第三种视图的面积为6或10.
12.B [解析]
∵1与6相对,4与x相对,5与y相对,∴1+6=4+x=5+y,∴x=3,y=2,
∴-xy=-32=-9.
13.B [解析]
选项A和C涂有颜色的面是底面,不能折叠成原几何体的形式;选项B能折叠成原几何体的形式;选项D中的图形不是这个几何体的表面展开图.故选B.
14.B [解析]
由三视图可知,该几何体是长方体,中间是空心圆柱,长方体的长、宽、高分别为4,4,3,圆柱底面圆直径为2,高为3,则长方体的表面积为4×4×2+4×3×4=80,圆柱的侧面积为2π×3=6π,上、下表面空心圆的面积和为2π,∴这个几何体的表面积是80+6π-2π=80+4π.
15.A [解析]
如图,2+2+1=5,故选A.
16.B [解析]首先画出圆柱的侧面展开图,根据高BC=6
cm,PC=BC,求出PC=×6=4(cm).在Rt△ACP中,根据勾股定理求出AP的长即可.具体的解答过程如下:
侧面展开图如图所示,
∵圆柱的底面周长为6
cm,
∴AC=3
cm.
∵PC=BC,
∴PC=×6=4(cm).
在Rt△ACP中,AP2=AC2+PC2,
∴AP==5(cm).
故选B.
17.6 [解析]
实际动手折一个正方体,将数字标上即可得解.
18.(1)10 (2)1 [解析]
(1)这个几何体由10个小正方体组成;(2)最多可以拿掉1个小正方体.
19.(1)2a (2)2a [解析]
(1)根据摆放情况可得,包装盒的一个长等于两个宽,即长为2a;(2)包装盒的长为2a,大纸箱的长为4a,宽为3a,图②中阴影部分的周长为3a×2+2a×2+2a=12a,图③中阴影部分的周长为4a×2+2a=10a,图②中阴影部分的周长与图③中阴影部分的周长的差为12a-10a=2a.
20.解:(1)如图所示:
(2)表面积为(5+5+3)×2+2=26+2=28.
21.解:(1)4
(2)如图所示:
22.解:(1)如图所示,连接CE,过点A作AF∥CE交BD于点F,则BF即为所求.
(2)∵AF∥CE,
∴∠AFB=∠CED.
又∵∠ABF=∠CDE=90°,
∴△ABF∽△CDE,
∴=,即=,
解得AB=8(米).
答:旗杆AB的高为8
米.
23.解:(1)F [解析]
A面与F面是对面,所以如果A面在长方体的底部,那么F面会在上面.
(2)这个长方体的表面积是2×(1×3+1×2+2×3)=22(米2);
这个长方体的体积是1×2×3=6(米3).
24.解:(1)如图,点O为灯的位置,QF为丙物体的影子.
(2)如图,作OM⊥QH于点M,设OM=x米,BM=y米.
由△GAB∽△GOM,得=,即=.①
由△CDH∽△OMH,得=,即=.②
由①-②×2,得=,解得y=0.6.
把y=0.6代入①,得x=4.8.
经检验,x=4.8,y=0.6是方程①②的解.
答:灯的高度为4.8米.
25.解:(1)平行
(2)如图,分别过点E,G作EM⊥AB,GN⊥CD,垂足分别是M,N,
则有△AEM∽△CGN,MB=EF=2米,ME=BF=10米,ND=GH=3米,
NG=DH=5米,∴AM=AB-MB=10-2=8(米),CN=CD-ND=(CD-3)米.
∵△CGN∽△AEM,∴=,即=,解得CD=7(米),即电线杆的高度是7米.
26.解:(1)画出图①中A—E1—C1,A—E2—C1,A—E3—C1,A—E4—C1中任意一条路径均可(E1,E2,E3,E4分别为各棱的中点).
(2)如图②,昆虫乙爬行的最短路程为AC1==10(cm),故昆虫乙至少需要爬行10÷2=5(秒).
(3)由(1)可知,当昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙可以沿下列四种路径中的任意一种爬行:
可以看出,图③与图④中的路径相等,图⑤与图⑥中的路径相等.
设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E1→F爬行捕捉到昆虫甲需x秒.如图③,在Rt△ACF中,(2x)2=(10-x)2+202,解得x=10(负值已舍去);
设昆虫甲从顶点C1沿棱C1C向顶点C爬行的同时,昆虫乙从顶点A按路径A→E2→F爬行捕捉到昆虫甲需y秒.如图⑤,在Rt△ADF中,(2y)2=(20-y)2+102,解得y≈8(负值已舍去).
综上,昆虫乙至少需要爬行约8秒才能捕捉到昆虫甲.
