冀教版九年级数学下第三十一章随机事件的概率巩固检测题(word版含答案)
文档属性
| 名称 | 冀教版九年级数学下第三十一章随机事件的概率巩固检测题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 259.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 19:38:49 | ||
图片预览




文档简介
冀教版九年级数学下第三十一章随机事件的概率巩固检测题
[时间:120分钟 分值:120分]
一、选择题(本大题共16个小题,共42分.1~10小题,每小题3分;11~16小题,每小题2分.在每小题给出的四个选项中,只有一项符合题目要求)
1.有下列事件:
①掷一次骰子,向上一面的点数是3;
②从一个只装有黑色球的袋子里摸出一个球,摸到的是白球;
③13个人中至少有两个人的生日是在同一个月份;
④射击运动员射击一次,命中靶心;
⑤水中捞月.
其中是必然事件的有
( )
A.1个
B.2个
C.3个
D.4个
2.下列对“某市明天下雨的概率是75%”这句话的理解正确的是
( )
A.该市明天将有75%的时间下雨
B.该市明天将有75%的地区下雨
C.该市明天一定下雨
D.该市明天下雨的可能性较大
3.如图1,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向蓝色区域的概率是
( )
图1
A.
B.C.
D.
4.在“绿水青山就是金山银山”这句话中任选一个汉字,这个字是“山”的概率为
( )
A.
B.
C.
D.
5.掷一枚质地均匀的骰子,骰子停止后,在下列四个选项中,可能性最大的是
( )
A.点数小于4
B.点数大于4
C.点数大于5
D.点数小于5
6.下列事件的概率,与“任意选2个人,恰好同月过生日”这一事件的概率相等的是( )
A.任意选2个人,恰好生肖相同
B.任意选2个人,恰好同一天过生日
C.任意掷2枚骰子,恰好朝上的点数相同
D.任意掷2枚硬币,恰好朝上的一面相同
7.某学习小组做抛掷一枚纪念币的试验,整理同学们获得的试验数据,如下表:
抛掷次数
50
100
200
500
1000
2000
3000
4000
5000
“正面向上”
的次数
19
38
68
168
349
707
1069
1400
1747
“正面向上”
的频率
0.3800
0.3800
0.3400
0.3360
0.3490
0.3535
0.3563
0.3500
0.3494
下面有三个推断:
①通过上述试验的结果,可以推断这枚纪念币有很大的可能性不是质地均匀的;
②如果再次做此试验,仍按上表抛掷的次数统计数据,那么在数据表中,“正面向上”的频率有更大的可能仍会在0.35附近摆动;
③在用频率估计概率时,用试验5000次时的频率0.3494一定比用试验4000次时的频率0.3500更准确.
其中正确的是
( )
A.①③
B.①②
C.②③
D.①②③
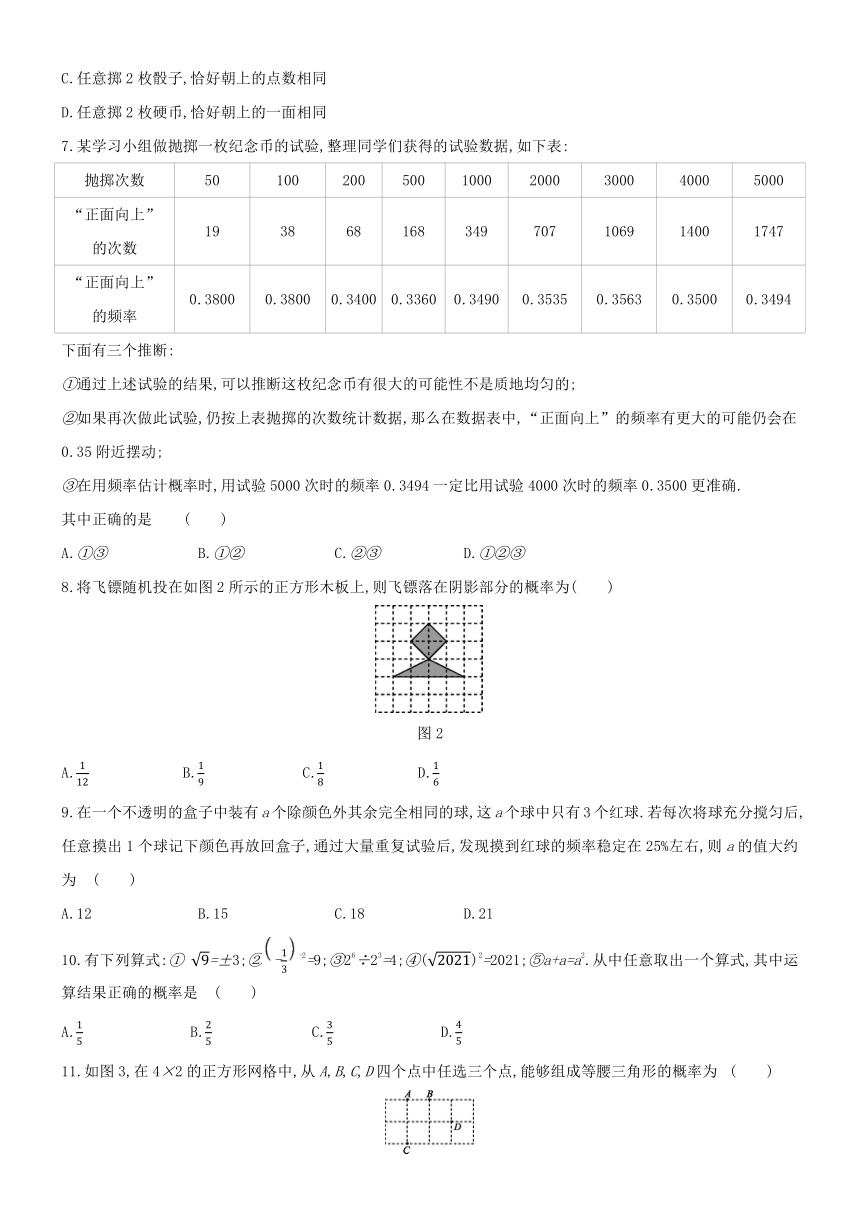
8.将飞镖随机投在如图2所示的正方形木板上,则飞镖落在阴影部分的概率为( )
图2
A.
B.
C.
D.
9.在一个不透明的盒子中装有a个除颜色外其余完全相同的球,这a个球中只有3个红球.若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,发现摸到红球的频率稳定在25%左右,则a的值大约为
( )
A.12
B.15
C.18
D.21
10.有下列算式:①
=±3;②--2=9;③26÷23=4;④()2=2021;⑤a+a=a2.从中任意取出一个算式,其中运算结果正确的概率是
( )
A.
B.
C.
D.
11.如图3,在4×2的正方形网格中,从A,B,C,D四个点中任选三个点,能够组成等腰三角形的概率为
( )
图3
A.0
B.
C.
D.
12.如图4,小球从A口往下落,在每个交叉口都有向左或向右两种可能,且可能性相同,则小球最终从E口落出的概率为
( )
图4
A.
B.
C.
D.
13.某校组织社团活动,小明和小刚从“数学社团”“航模社团”“文艺社团”三个社团中,随机选择一个社团参加活动,两人恰好选择同一个社团的概率是
( )
A.
B.
C.
D.
14.一个不透明的盒子里只装有白色和红色两种颜色的球,这些球除颜色外没有其他不同.若从盒子里随机摸取一个球,有三种可能性相等的结果,设摸到红球的概率为P,则P的值为( )
A.
B.
C.或
D.或
15.有四张背面相同的扑克牌,分别为红桃1,2,3,4,背面朝上,先从中抽取一张,把抽到的点数记为a,再在剩余的扑克牌中抽取一张,把抽到的点数记为b,则点(a,b)在直线y=x+1上方的概率是
( )
A.
B.
C.
D.
16.甲、乙是两个不透明的纸箱,甲中有三张标有数字,,1的卡片,乙中有三张标有数字1,2,3的卡片,卡片除所标数字外,无其他差别.现制定一个游戏规则:从甲中任取一张卡片,将其数字记为a,从乙中任取一张卡片,将其数字记为b,若a,b能使关于x的一元二次方程ax2+bx+1=0有两个不相等的实数根,则甲获胜;否则乙获胜.那么乙获胜的概率为
( )
A.
B.
C.
D.
二、填空题(本大题共3个小题,共11分.17小题3分,18~19小题各有两个空,每空2分,把答案写在题中横线上)
17.有下列事件:①明天空气质量良好;②两次抛掷一枚质地均匀的正方体骰子(六个面上分别标有数字1,2,3,4,5,6),掷得的数字之和小于13;③从一只仅装有红球的口袋中,任意摸出一个球,恰是白球;
④抛掷硬币50次,第50次正面向上.其中为确定事件的是
.(填正确答案的序号)?
18.在一个不透明的盒子里装有黑、白两种颜色的球共50个,这些球除颜色外其余完全相同.王颖做摸球试验,搅匀后,她从盒子里随机摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程.下表是试验中的一组统计数据:
摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
65
124
178
302
480
600
1800
摸到白球的频率
0.650
0.620
0.593
0.604
0.600
0.600
0.600
(1)若从盒子里随机摸出一个球,则摸到白球的概率的估计值为 (精确到0.1);?
(2)估计盒子里黑球有 个.?
19.小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一道题不使用“求助”,那么小明答对第一道题的概率是 ;?
(2)如果小明将“求助”留在第二道题使用,那么小明顺利通关的概率是 .?
三、解答题(本大题共7小题,共67分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8分)一只不透明的袋子中装有1个白球、2个黄球和3个红球,每个球除颜色外其余都相同,将球摇匀.
(1)如果从中任意摸出一个球:
①你能够事先确定摸到的球的颜色吗?
②你认为摸到哪种颜色的球的概率最大?
③如何改变袋中白球、红球的个数,使摸到这三种颜色的球的概率相等?
(2)从中一次性最少摸出 个球,必然会有红色的球.?
21.(本小题满分9分)一个不透明的盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀.重复进行这样的试验得到以下数据:
摸棋次数n
100
200
300
500
800
1000
摸到黑棋的次数m
24
51
76
124
201
250
摸到黑棋的频率
(精确到0.001)
0.240
0.255
0.253
0.248
0.251
0.250
(1)根据表中数据估计从盒中摸出一枚棋是黑棋的概率是 (精确到0.01);?
(2)若盒中黑棋与白棋共有4枚,某同学一次摸出两枚棋,请估算这两枚棋颜色不同的概率.
22.(本小题满分9分)如图5,有四张质地完全相同的卡片,正面分别写有一个角度,现将这四张卡片洗匀后,背面朝上.
(1)若从中任意抽取一张,求抽到锐角卡片的概率;
(2)若从中任意抽取两张,求抽到的两张角度恰好互补的概率.
图5
23.(本小题满分9分)若一个三位数的十位数字比个位数字和百位数字都大,则称这个数为“伞数”.现从1,2,3,4这四个数字中任取3个数,组成无重复数字的三位数.
(1)请画出树形图并写出所有可能得到的三位数.
(2)甲、乙二人玩一个游戏,游戏规则是若组成的三位数是“伞数”,则甲胜;否则乙胜.你认为这个游戏公平吗?试说明理由.
24.(本小题满分10分)光明中学以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨举办首届《诗词大会》,九年级(2)班的马小梅晋级总决赛,比赛过程分两个环节,参赛选手须在每个环节中各选择一道题目.第一环节:横扫千军、你说我猜、初级飞花令(分别用T1,T2,T3表示);第二环节:出口成诗、飞花令、超级飞花令、诗词接龙(分别用S1,S2,S3,S4表示).
(1)请用画树形图或列表的方法表示马小梅参加总决赛抽取题目的所有可能结果;
(2)求马小梅参加总决赛抽取题目都是飞花令题目(初级飞花令、飞花令、超级飞花令)的概率.
25.(本小题满分10分)阅读材料,回答问题.
材料:
题1:经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性的大小相同,求三辆汽车经过这个十字路口时,至少有两辆车向左转的概率.
题2:有两把不同的锁和三把钥匙,其中两把钥匙分别能打开这两把锁(一把钥匙只能开一把锁),第三把钥匙不能打开这两把锁.随机取出一把钥匙开任意一把锁,一次打开锁的概率是多少?
我们可以用“袋中摸球”的试验来模拟题1:在不透明的口袋中放三个不同颜色的小球(小球除颜色外其余均相同),红球表示直行,绿球表示向左转,黑球表示向右转,三辆汽车经过路口,相当于从三个这样的口袋中各随机摸出一个球.
问题:
(1)事件“至少有两辆车向左转”相当于“袋中摸球”的试验中的什么事件?
(2)设计一个“袋中摸球”的试验来模拟题2,请简要说明你的方案;
(3)请直接写出题2的结果.
26.(本小题满分12分)李莉在五张完全相同并且没有任何标记的卡片的一面分别写下数字-4,-1,0,3,5,将写有数字的一面朝下放置,并混合均匀.
(1)随机摸取一张,求上面的数字为负数的概率;
(2)随机摸取两张,其中一张表示x,另一张表示y,求点(x,y)在直线y=-x-1上的概率;
(3)随机摸取一张,记为x,然后放回,混合均匀后再随机摸取一张,记为y,求点(x,y)是第四象限内的点的概率.
参考答案
1.A [解析]
①掷一次骰子,向上一面的点数是3,是随机事件;
②从一个只装有黑色球的袋子里摸出一个球,摸到的是白球,是不可能事件;
③13个人中至少有两个人的生日是在同一个月份,是必然事件;
④射击运动员射击一次,命中靶心,是随机事件;
⑤水中捞月,是不可能事件.
故选A.
2.D
3.D [解析]
∵一个可以自由转动的转盘被等分成6个扇形区域,其中蓝色部分占2份,∴指针指向蓝色区域的概率是==.故选D.
4.A [解析]
∵在“绿水青山就是金山银山”这10个字中,“山”字有3个,∴在这句话中任选一个汉字,这个字是“山”的概率是.
5.D [解析]
掷一枚质地均匀的骰子,骰子停止后共有6种等可能的情况,即点数为1,2,3,4,5,6.其中点数小于4的有3种,点数大于4的有2种,点数大于5的有1种,点数小于5的有4种,故点数小于5的可能性较大,故选D.
6.A [解析]
“任意选2个人,恰好同月过生日”的概率为,“任意选2个人,恰好生肖相同”的概率也是,因此“任意选2个人,恰好同月过生日”这一事件的概率与“任意选2个人,恰好生肖相同”这一事件的概率相同.
7.B
8.B [解析]
∵总面积为6×6=36,其中阴影部分的面积为2+×1×4=4,∴飞镖落在阴影部分的概率是=.
9.A [解析]
由题意,得×100%=25%,解得a=12.经检验a=12是原分式方程的解.
10.B [解析]
①=3,故错误;
②--2==9,正确;
③26÷23=23=8,故错误;
④()2=2021,正确;
⑤a+a=2a,故错误.
故从中任意取出一个算式,其中运算结果正确的概率是.
11.B [解析]
从A,B,C,D四个点中任选三个点,有如下四种情况:ABC,ABD,ACD,BCD,其中能够组成等腰三角形的有ACD,BCD两种情况,∴能够组成等腰三角形的概率为=.
12.B
13.A
14.D [解析]
由题意可得,这个袋子中有三个球,可能是一红两白,也可能是两红一白,当袋子中的球是一红两白时,P=,当袋子中的球是两红一白时,P=,故选D.
15.C [解析]
画树形图如下:
由树形图可知一共有12种等可能的结果,其中点(a,b)在直线y=x+1上方的有3种结果,所以点(a,b)在直线y=x+1上方的概率为=,故选C.
16.C [解析]
画树形图如下:
由图可知共有9种等可能的结果.其中能使乙获胜的有4种,∴乙获胜的概率为.
17.②③ [解析]
①④是随机事件;②是必然事件;③是不可能事件.故确定事件是②③.
18.(1)0.6 (2)20 [解析]
(1)当n很大时,摸到白球的频率稳定于0.6,∴若从盒子里随机摸出一个球,则摸到白球的概率的估计值为0.6.
(2)黑、白球共有50个,白球为50×0.6=30(个),则黑球为50-30=20(个).
19.(1) (2) [解析]
(1)∵第一道单选题有3个选项,∴小明第一道题不使用“求助”,那么小明答对第一道题的概率是.
(2)分别用A,B,C表示第一道单选题的3个选项,a,b,c表示第二道单选题剩下的3个选项,画树形图,得
∵共有9种等可能的结果,小明顺利通关的结果只有1种,
∴小明顺利通关的概率为.
20.解:(1)①不能事先确定摸到的球的颜色.
②摸到红球的概率最大.
③增加1个白球,减少1个红球就能使摸到这三种颜色的球的概率相等.
(2)4
21.解:(1)0.25
(2)由(1)可估计,黑棋有4×0.25=1(枚),则白棋有3枚,画树形图如下:
由图可知,所有等可能结果共有12种,其中这两枚棋颜色不同的有6种结果,所以估计这两枚棋颜色不同的概率为.
22.解:(1)一共有四张卡片,其中写有锐角的卡片有两张,因此P(抽到锐角卡片)==.
(2)列表如下:
36°
54°
144°
126°
36°
90°
180°
162°
54°
90°
198°
180°
144°
180°
198°
270°
126°
162°
180°
270°
由表可知一共有12种等可能的结果,其中互补的结果有4种,所以P(抽到的两张角度恰好互补)==.
23.解:(1)画树形图如下:
所有可能得到的三位数有24个,分别为123,124,132,134,142,143,213,214,
231,234,241,243,312,314,321,324,341,342,412,413,421,423,431,432.
(2)这个游戏不公平.
理由如下:组成的三位数中是“伞数”的有132,142,143,231,241,243,341,342,共8个,所以甲胜的概率为=,而乙胜的概率为=,故这个游戏不公平.
24.解:(1)马小梅参加总决赛抽取题目的所有可能结果如下表:
第二环节
第一环节
S1
S2
S3
S4
T1
(T1,S1)
(T1,S2)
(T1,S3)
(T1,S4)
T2
(T2,S1)
(T2,S2)
(T2,S3)
(T2,S4)
T3
(T3,S1)
(T3,S2)
(T3,S3)
(T3,S4)
(2)由题意可知,T3,S2,S3代表飞花令题目,由(1)知总共有12种等可能的结果,马小梅参加总决赛抽取题目都是飞花令题目的有(T3,S2),(T3,S3)共2种情况,所以所求概率为.
25.解:(1)至少摸出两个绿球.
(2)一个不透明的口袋中放红色和黑色的小球各一个(小球除颜色外其余均相同),分别表示不同的锁,另一个不透明的口袋中放红色、黑色和绿色的小球各一个(小球除颜色外其余均相同),分别表示不同的钥匙,其中同颜色的球表示一套锁和钥匙.“随机取出一把钥匙开任意一把锁,一次打开锁的概率”相当于“从两个口袋中各随机摸出一个球,两球颜色一样的概率”(答案合理即可).
(3)
26.解:(1)上面的数字为负数的概率为.
(2)画树形图如图所示:
一共有20种等可能的结果,点(x,y)在直线y=-x-1上的结果有4种,
∴点(x,y)在直线y=-x-1上的概率为=.
(3)画树形图如图所示:
一共有25种等可能的结果,点(x,y)在第四象限内的结果有4种,
∴点(x,y)是第四象限内的点的概率为.
[时间:120分钟 分值:120分]
一、选择题(本大题共16个小题,共42分.1~10小题,每小题3分;11~16小题,每小题2分.在每小题给出的四个选项中,只有一项符合题目要求)
1.有下列事件:
①掷一次骰子,向上一面的点数是3;
②从一个只装有黑色球的袋子里摸出一个球,摸到的是白球;
③13个人中至少有两个人的生日是在同一个月份;
④射击运动员射击一次,命中靶心;
⑤水中捞月.
其中是必然事件的有
( )
A.1个
B.2个
C.3个
D.4个
2.下列对“某市明天下雨的概率是75%”这句话的理解正确的是
( )
A.该市明天将有75%的时间下雨
B.该市明天将有75%的地区下雨
C.该市明天一定下雨
D.该市明天下雨的可能性较大
3.如图1,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向蓝色区域的概率是
( )
图1
A.
B.C.
D.
4.在“绿水青山就是金山银山”这句话中任选一个汉字,这个字是“山”的概率为
( )
A.
B.
C.
D.
5.掷一枚质地均匀的骰子,骰子停止后,在下列四个选项中,可能性最大的是
( )
A.点数小于4
B.点数大于4
C.点数大于5
D.点数小于5
6.下列事件的概率,与“任意选2个人,恰好同月过生日”这一事件的概率相等的是( )
A.任意选2个人,恰好生肖相同
B.任意选2个人,恰好同一天过生日
C.任意掷2枚骰子,恰好朝上的点数相同
D.任意掷2枚硬币,恰好朝上的一面相同
7.某学习小组做抛掷一枚纪念币的试验,整理同学们获得的试验数据,如下表:
抛掷次数
50
100
200
500
1000
2000
3000
4000
5000
“正面向上”
的次数
19
38
68
168
349
707
1069
1400
1747
“正面向上”
的频率
0.3800
0.3800
0.3400
0.3360
0.3490
0.3535
0.3563
0.3500
0.3494
下面有三个推断:
①通过上述试验的结果,可以推断这枚纪念币有很大的可能性不是质地均匀的;
②如果再次做此试验,仍按上表抛掷的次数统计数据,那么在数据表中,“正面向上”的频率有更大的可能仍会在0.35附近摆动;
③在用频率估计概率时,用试验5000次时的频率0.3494一定比用试验4000次时的频率0.3500更准确.
其中正确的是
( )
A.①③
B.①②
C.②③
D.①②③
8.将飞镖随机投在如图2所示的正方形木板上,则飞镖落在阴影部分的概率为( )
图2
A.
B.
C.
D.
9.在一个不透明的盒子中装有a个除颜色外其余完全相同的球,这a个球中只有3个红球.若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,发现摸到红球的频率稳定在25%左右,则a的值大约为
( )
A.12
B.15
C.18
D.21
10.有下列算式:①
=±3;②--2=9;③26÷23=4;④()2=2021;⑤a+a=a2.从中任意取出一个算式,其中运算结果正确的概率是
( )
A.
B.
C.
D.
11.如图3,在4×2的正方形网格中,从A,B,C,D四个点中任选三个点,能够组成等腰三角形的概率为
( )
图3
A.0
B.
C.
D.
12.如图4,小球从A口往下落,在每个交叉口都有向左或向右两种可能,且可能性相同,则小球最终从E口落出的概率为
( )
图4
A.
B.
C.
D.
13.某校组织社团活动,小明和小刚从“数学社团”“航模社团”“文艺社团”三个社团中,随机选择一个社团参加活动,两人恰好选择同一个社团的概率是
( )
A.
B.
C.
D.
14.一个不透明的盒子里只装有白色和红色两种颜色的球,这些球除颜色外没有其他不同.若从盒子里随机摸取一个球,有三种可能性相等的结果,设摸到红球的概率为P,则P的值为( )
A.
B.
C.或
D.或
15.有四张背面相同的扑克牌,分别为红桃1,2,3,4,背面朝上,先从中抽取一张,把抽到的点数记为a,再在剩余的扑克牌中抽取一张,把抽到的点数记为b,则点(a,b)在直线y=x+1上方的概率是
( )
A.
B.
C.
D.
16.甲、乙是两个不透明的纸箱,甲中有三张标有数字,,1的卡片,乙中有三张标有数字1,2,3的卡片,卡片除所标数字外,无其他差别.现制定一个游戏规则:从甲中任取一张卡片,将其数字记为a,从乙中任取一张卡片,将其数字记为b,若a,b能使关于x的一元二次方程ax2+bx+1=0有两个不相等的实数根,则甲获胜;否则乙获胜.那么乙获胜的概率为
( )
A.
B.
C.
D.
二、填空题(本大题共3个小题,共11分.17小题3分,18~19小题各有两个空,每空2分,把答案写在题中横线上)
17.有下列事件:①明天空气质量良好;②两次抛掷一枚质地均匀的正方体骰子(六个面上分别标有数字1,2,3,4,5,6),掷得的数字之和小于13;③从一只仅装有红球的口袋中,任意摸出一个球,恰是白球;
④抛掷硬币50次,第50次正面向上.其中为确定事件的是
.(填正确答案的序号)?
18.在一个不透明的盒子里装有黑、白两种颜色的球共50个,这些球除颜色外其余完全相同.王颖做摸球试验,搅匀后,她从盒子里随机摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程.下表是试验中的一组统计数据:
摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
65
124
178
302
480
600
1800
摸到白球的频率
0.650
0.620
0.593
0.604
0.600
0.600
0.600
(1)若从盒子里随机摸出一个球,则摸到白球的概率的估计值为 (精确到0.1);?
(2)估计盒子里黑球有 个.?
19.小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一道题不使用“求助”,那么小明答对第一道题的概率是 ;?
(2)如果小明将“求助”留在第二道题使用,那么小明顺利通关的概率是 .?
三、解答题(本大题共7小题,共67分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分8分)一只不透明的袋子中装有1个白球、2个黄球和3个红球,每个球除颜色外其余都相同,将球摇匀.
(1)如果从中任意摸出一个球:
①你能够事先确定摸到的球的颜色吗?
②你认为摸到哪种颜色的球的概率最大?
③如何改变袋中白球、红球的个数,使摸到这三种颜色的球的概率相等?
(2)从中一次性最少摸出 个球,必然会有红色的球.?
21.(本小题满分9分)一个不透明的盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀.重复进行这样的试验得到以下数据:
摸棋次数n
100
200
300
500
800
1000
摸到黑棋的次数m
24
51
76
124
201
250
摸到黑棋的频率
(精确到0.001)
0.240
0.255
0.253
0.248
0.251
0.250
(1)根据表中数据估计从盒中摸出一枚棋是黑棋的概率是 (精确到0.01);?
(2)若盒中黑棋与白棋共有4枚,某同学一次摸出两枚棋,请估算这两枚棋颜色不同的概率.
22.(本小题满分9分)如图5,有四张质地完全相同的卡片,正面分别写有一个角度,现将这四张卡片洗匀后,背面朝上.
(1)若从中任意抽取一张,求抽到锐角卡片的概率;
(2)若从中任意抽取两张,求抽到的两张角度恰好互补的概率.
图5
23.(本小题满分9分)若一个三位数的十位数字比个位数字和百位数字都大,则称这个数为“伞数”.现从1,2,3,4这四个数字中任取3个数,组成无重复数字的三位数.
(1)请画出树形图并写出所有可能得到的三位数.
(2)甲、乙二人玩一个游戏,游戏规则是若组成的三位数是“伞数”,则甲胜;否则乙胜.你认为这个游戏公平吗?试说明理由.
24.(本小题满分10分)光明中学以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨举办首届《诗词大会》,九年级(2)班的马小梅晋级总决赛,比赛过程分两个环节,参赛选手须在每个环节中各选择一道题目.第一环节:横扫千军、你说我猜、初级飞花令(分别用T1,T2,T3表示);第二环节:出口成诗、飞花令、超级飞花令、诗词接龙(分别用S1,S2,S3,S4表示).
(1)请用画树形图或列表的方法表示马小梅参加总决赛抽取题目的所有可能结果;
(2)求马小梅参加总决赛抽取题目都是飞花令题目(初级飞花令、飞花令、超级飞花令)的概率.
25.(本小题满分10分)阅读材料,回答问题.
材料:
题1:经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性的大小相同,求三辆汽车经过这个十字路口时,至少有两辆车向左转的概率.
题2:有两把不同的锁和三把钥匙,其中两把钥匙分别能打开这两把锁(一把钥匙只能开一把锁),第三把钥匙不能打开这两把锁.随机取出一把钥匙开任意一把锁,一次打开锁的概率是多少?
我们可以用“袋中摸球”的试验来模拟题1:在不透明的口袋中放三个不同颜色的小球(小球除颜色外其余均相同),红球表示直行,绿球表示向左转,黑球表示向右转,三辆汽车经过路口,相当于从三个这样的口袋中各随机摸出一个球.
问题:
(1)事件“至少有两辆车向左转”相当于“袋中摸球”的试验中的什么事件?
(2)设计一个“袋中摸球”的试验来模拟题2,请简要说明你的方案;
(3)请直接写出题2的结果.
26.(本小题满分12分)李莉在五张完全相同并且没有任何标记的卡片的一面分别写下数字-4,-1,0,3,5,将写有数字的一面朝下放置,并混合均匀.
(1)随机摸取一张,求上面的数字为负数的概率;
(2)随机摸取两张,其中一张表示x,另一张表示y,求点(x,y)在直线y=-x-1上的概率;
(3)随机摸取一张,记为x,然后放回,混合均匀后再随机摸取一张,记为y,求点(x,y)是第四象限内的点的概率.
参考答案
1.A [解析]
①掷一次骰子,向上一面的点数是3,是随机事件;
②从一个只装有黑色球的袋子里摸出一个球,摸到的是白球,是不可能事件;
③13个人中至少有两个人的生日是在同一个月份,是必然事件;
④射击运动员射击一次,命中靶心,是随机事件;
⑤水中捞月,是不可能事件.
故选A.
2.D
3.D [解析]
∵一个可以自由转动的转盘被等分成6个扇形区域,其中蓝色部分占2份,∴指针指向蓝色区域的概率是==.故选D.
4.A [解析]
∵在“绿水青山就是金山银山”这10个字中,“山”字有3个,∴在这句话中任选一个汉字,这个字是“山”的概率是.
5.D [解析]
掷一枚质地均匀的骰子,骰子停止后共有6种等可能的情况,即点数为1,2,3,4,5,6.其中点数小于4的有3种,点数大于4的有2种,点数大于5的有1种,点数小于5的有4种,故点数小于5的可能性较大,故选D.
6.A [解析]
“任意选2个人,恰好同月过生日”的概率为,“任意选2个人,恰好生肖相同”的概率也是,因此“任意选2个人,恰好同月过生日”这一事件的概率与“任意选2个人,恰好生肖相同”这一事件的概率相同.
7.B
8.B [解析]
∵总面积为6×6=36,其中阴影部分的面积为2+×1×4=4,∴飞镖落在阴影部分的概率是=.
9.A [解析]
由题意,得×100%=25%,解得a=12.经检验a=12是原分式方程的解.
10.B [解析]
①=3,故错误;
②--2==9,正确;
③26÷23=23=8,故错误;
④()2=2021,正确;
⑤a+a=2a,故错误.
故从中任意取出一个算式,其中运算结果正确的概率是.
11.B [解析]
从A,B,C,D四个点中任选三个点,有如下四种情况:ABC,ABD,ACD,BCD,其中能够组成等腰三角形的有ACD,BCD两种情况,∴能够组成等腰三角形的概率为=.
12.B
13.A
14.D [解析]
由题意可得,这个袋子中有三个球,可能是一红两白,也可能是两红一白,当袋子中的球是一红两白时,P=,当袋子中的球是两红一白时,P=,故选D.
15.C [解析]
画树形图如下:
由树形图可知一共有12种等可能的结果,其中点(a,b)在直线y=x+1上方的有3种结果,所以点(a,b)在直线y=x+1上方的概率为=,故选C.
16.C [解析]
画树形图如下:
由图可知共有9种等可能的结果.其中能使乙获胜的有4种,∴乙获胜的概率为.
17.②③ [解析]
①④是随机事件;②是必然事件;③是不可能事件.故确定事件是②③.
18.(1)0.6 (2)20 [解析]
(1)当n很大时,摸到白球的频率稳定于0.6,∴若从盒子里随机摸出一个球,则摸到白球的概率的估计值为0.6.
(2)黑、白球共有50个,白球为50×0.6=30(个),则黑球为50-30=20(个).
19.(1) (2) [解析]
(1)∵第一道单选题有3个选项,∴小明第一道题不使用“求助”,那么小明答对第一道题的概率是.
(2)分别用A,B,C表示第一道单选题的3个选项,a,b,c表示第二道单选题剩下的3个选项,画树形图,得
∵共有9种等可能的结果,小明顺利通关的结果只有1种,
∴小明顺利通关的概率为.
20.解:(1)①不能事先确定摸到的球的颜色.
②摸到红球的概率最大.
③增加1个白球,减少1个红球就能使摸到这三种颜色的球的概率相等.
(2)4
21.解:(1)0.25
(2)由(1)可估计,黑棋有4×0.25=1(枚),则白棋有3枚,画树形图如下:
由图可知,所有等可能结果共有12种,其中这两枚棋颜色不同的有6种结果,所以估计这两枚棋颜色不同的概率为.
22.解:(1)一共有四张卡片,其中写有锐角的卡片有两张,因此P(抽到锐角卡片)==.
(2)列表如下:
36°
54°
144°
126°
36°
90°
180°
162°
54°
90°
198°
180°
144°
180°
198°
270°
126°
162°
180°
270°
由表可知一共有12种等可能的结果,其中互补的结果有4种,所以P(抽到的两张角度恰好互补)==.
23.解:(1)画树形图如下:
所有可能得到的三位数有24个,分别为123,124,132,134,142,143,213,214,
231,234,241,243,312,314,321,324,341,342,412,413,421,423,431,432.
(2)这个游戏不公平.
理由如下:组成的三位数中是“伞数”的有132,142,143,231,241,243,341,342,共8个,所以甲胜的概率为=,而乙胜的概率为=,故这个游戏不公平.
24.解:(1)马小梅参加总决赛抽取题目的所有可能结果如下表:
第二环节
第一环节
S1
S2
S3
S4
T1
(T1,S1)
(T1,S2)
(T1,S3)
(T1,S4)
T2
(T2,S1)
(T2,S2)
(T2,S3)
(T2,S4)
T3
(T3,S1)
(T3,S2)
(T3,S3)
(T3,S4)
(2)由题意可知,T3,S2,S3代表飞花令题目,由(1)知总共有12种等可能的结果,马小梅参加总决赛抽取题目都是飞花令题目的有(T3,S2),(T3,S3)共2种情况,所以所求概率为.
25.解:(1)至少摸出两个绿球.
(2)一个不透明的口袋中放红色和黑色的小球各一个(小球除颜色外其余均相同),分别表示不同的锁,另一个不透明的口袋中放红色、黑色和绿色的小球各一个(小球除颜色外其余均相同),分别表示不同的钥匙,其中同颜色的球表示一套锁和钥匙.“随机取出一把钥匙开任意一把锁,一次打开锁的概率”相当于“从两个口袋中各随机摸出一个球,两球颜色一样的概率”(答案合理即可).
(3)
26.解:(1)上面的数字为负数的概率为.
(2)画树形图如图所示:
一共有20种等可能的结果,点(x,y)在直线y=-x-1上的结果有4种,
∴点(x,y)在直线y=-x-1上的概率为=.
(3)画树形图如图所示:
一共有25种等可能的结果,点(x,y)在第四象限内的结果有4种,
∴点(x,y)是第四象限内的点的概率为.
