人教版数学八年级上册 第13章 13.1轴对称同步测试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学八年级上册 第13章 13.1轴对称同步测试题(一)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 288.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 21:22:24 | ||
图片预览


文档简介
轴对称同步测试题(一)
一.选择题
1.我国民间,流传着许多含有吉祥意义的图案,表示对幸福生活的向往,良辰佳节的祝贺.比如下列图案分别表示“福”“禄”“寿”“喜”,其中是轴对称图形的有几个( )
A.1个 B.2个 C.3个 D.4个
2.如图,设L1和L2是镜面平行相对且间距为30cm的两面镜子,把一个小球A放在L1和L2之间,小球在镜L1中的像为A′,A′在镜L2中的像为A′′,则AA′′等于( )
A.10cm B.20cm C.40cm D.60cm
3.如图,从标有数字1,2,3,4的四个小正方形中拿走一个,成为一个轴对称图形,则应该拿走的小正方形的标号是( )
A.1 B.2 C.3 D.4
4.如图,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于点F,若∠FAC=65°,则∠B的度数为( )
A.45° B.50° C.65° D.60°
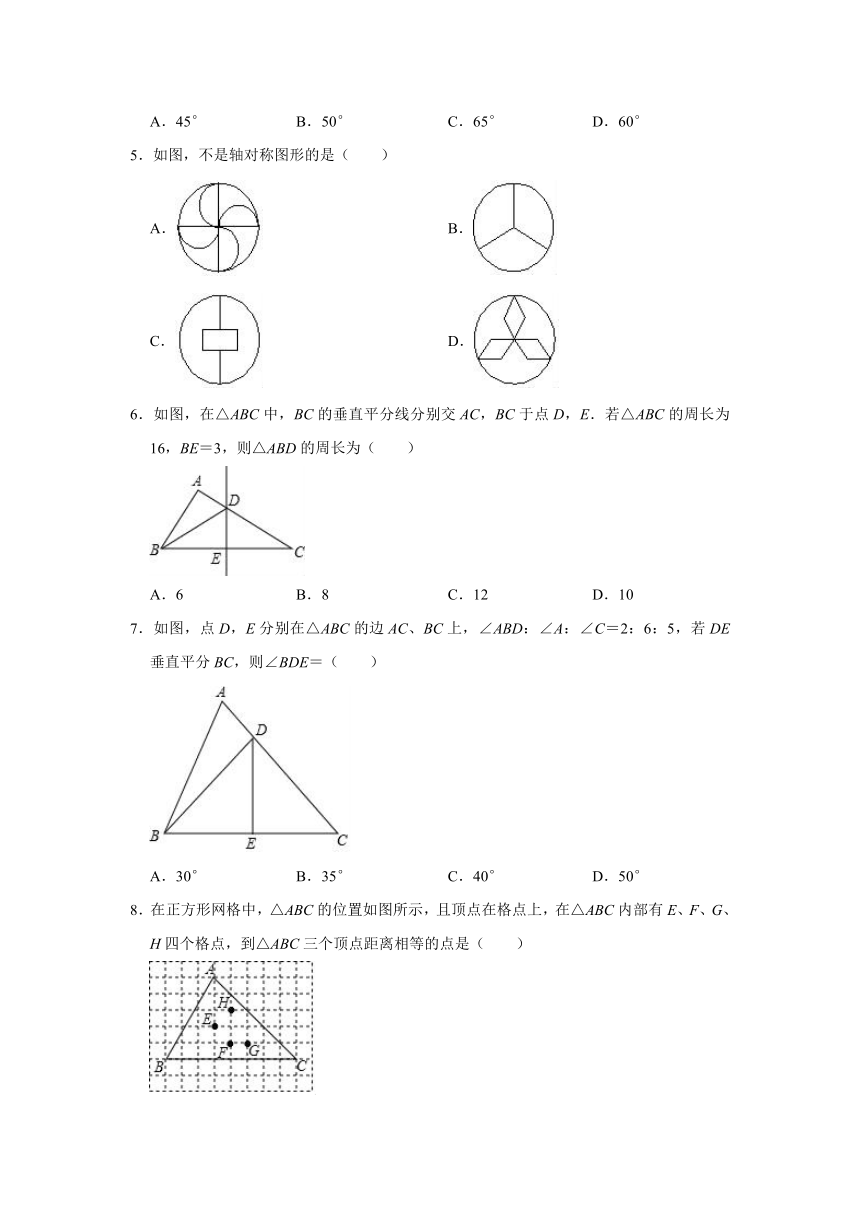
5.如图,不是轴对称图形的是( )
A. B.
C. D.
6.如图,在△ABC中,BC的垂直平分线分别交AC,BC于点D,E.若△ABC的周长为16,BE=3,则△ABD的周长为( )
A.6 B.8 C.12 D.10
7.如图,点D,E分别在△ABC的边AC、BC上,∠ABD:∠A:∠C=2:6:5,若DE垂直平分BC,则∠BDE=( )
A.30° B.35° C.40° D.50°
8.在正方形网格中,△ABC的位置如图所示,且顶点在格点上,在△ABC内部有E、F、G、H四个格点,到△ABC三个顶点距离相等的点是( )
A.点E B.点F C.点G D.点H
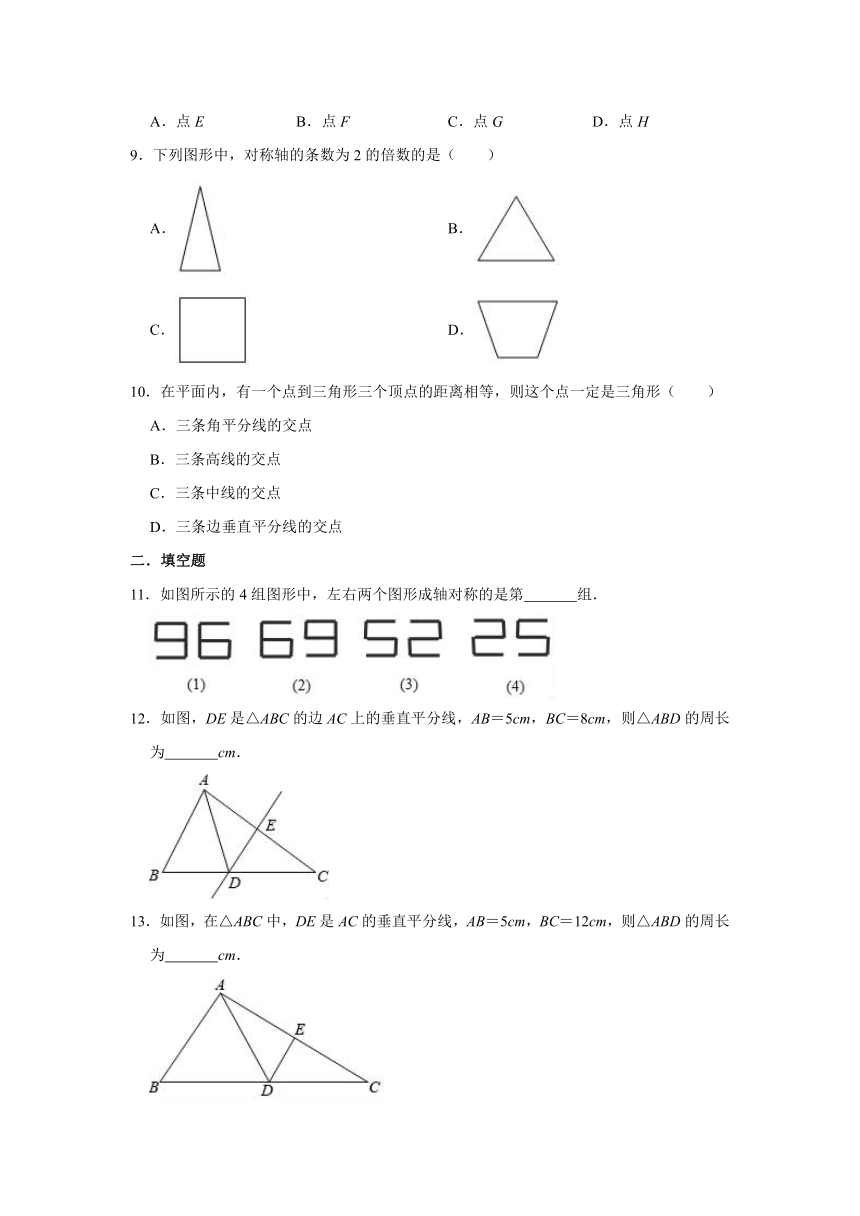
9.下列图形中,对称轴的条数为2的倍数的是( )
A. B.
C. D.
10.在平面内,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形( )
A.三条角平分线的交点
B.三条高线的交点
C.三条中线的交点
D.三条边垂直平分线的交点
二.填空题
11.如图所示的4组图形中,左右两个图形成轴对称的是第 组.
12.如图,DE是△ABC的边AC上的垂直平分线,AB=5cm,BC=8cm,则△ABD的周长为 cm.
13.如图,在△ABC中,DE是AC的垂直平分线,AB=5cm,BC=12cm,则△ABD的周长为 cm.
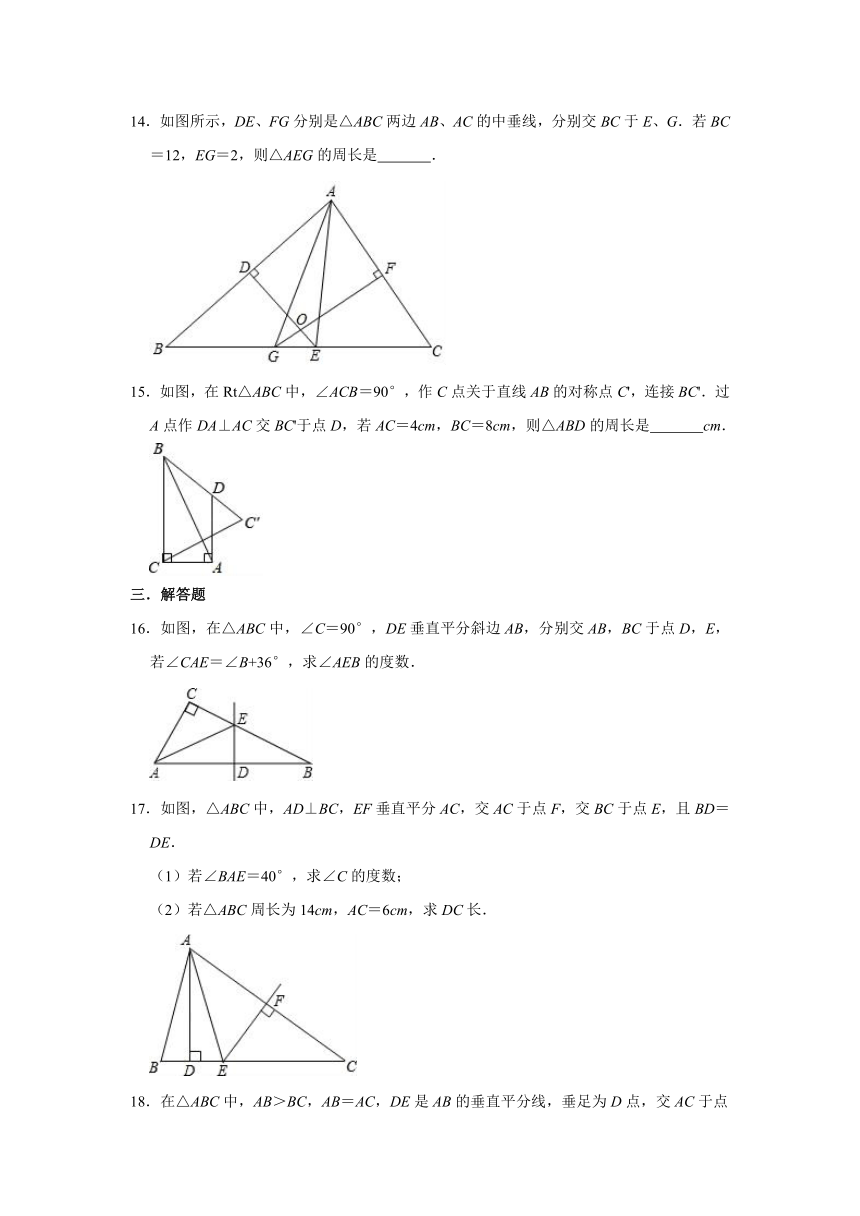
14.如图所示,DE、FG分别是△ABC两边AB、AC的中垂线,分别交BC于E、G.若BC=12,EG=2,则△AEG的周长是 .
15.如图,在Rt△ABC中,∠ACB=90°,作C点关于直线AB的对称点C',连接BC'.过A点作DA⊥AC交BC'于点D,若AC=4cm,BC=8cm,则△ABD的周长是 cm.
三.解答题
16.如图,在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB,BC于点D,E,若∠CAE=∠B+36°,求∠AEB的度数.
17.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
(1)若∠BAE=40°,求∠C的度数;
(2)若△ABC周长为14cm,AC=6cm,求DC长.
18.在△ABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D点,交AC于点E.
(1)若∠ABE=38°,求∠EBC的度数;
(2)若△ABC的周长为36cm,一边为13cm,求△BCE的周长.
19.如图,在△ABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE
(1)求∠ECD的度数;
(2)若∠ACB为α,则∠ECD的度数能否用含α的式子来表示.
参考答案与试题解析
一.选择题
1.【解答】解:第一个图形不是轴对称图形,
第二、三、四个图形是轴对称图形,
共3个轴对称图形,
故选:C.
2.【解答】解:如图所示,经过反射后,A'B=AB,A'C=CA'',
∴AA''=AC+A''C=AC+A'C=AC+2AB+AC=2BC=60cm.
故选:D.
3.【解答】解:从标有数字1,2,3,4的四个小正方形中拿走2,就可以成为一个轴对称图形.
故选:B.
4.【解答】解:∵AD是∠BAC的平分线,
∴∠CAD=∠BAD,
∵EF垂直平分AD,
∴FA=FD,
∴∠FDA=∠FAD=∠FAC+∠CAD,
∵∠FDA是△ABD的一个外角,
∴∠B=∠FDA﹣∠BAD=∠FDA﹣∠CAD=65°,
故选:C.
5.【解答】解:A、不是轴对称图形;
B、是轴对称图形;
C、是轴对称图形;
D、是轴对称图形;
故选:A.
6.【解答】解:∵DE是BC的垂直平分线,
∴DB=DC,BC=2BE=6,
∵△ABC的周长为16,
∴AB+BC+AC=16,
∴AB+AC=10,
∴△ABD的周长=AB+AD+BD=AB+AD+DC=AB+AC=10,
故选:D.
7.【解答】解:∵∠ABD:∠A:∠C=2:6:5,
∴设∠ABD=2k,∠A=6k,∠C=5k,
∵DE垂直平分BC,
∴BD=CD,
∴∠DBC=∠C=5k,
∴∠ABC=7k,
∵∠A+∠ABC+∠C=180°,
∴6k+7k+5k=180°,
∴k=10°,
∴∠DBE=50°,
∵∠DEB=90°,
∴∠BDE=40°,
故选:C.
8.【解答】解:∵BF=AF=CF==,
∴到△ABC三个顶点距离相等的点是F,
故选:B.
9.【解答】解:A、图形有一条对称轴,不符合题意;
B、图形有三条对称轴,不符合题意;
C、图形有四条对称轴,符合题意;
D、图形有一条对称轴,不符合题意;
故选:C.
10.【解答】解:∵点到三角形三个顶点的距离相等,
∴这个点一定是三角形三条边的垂直平分线的交点,
故选:D.
二.填空题(共5小题)
11.【解答】解:(1)不是轴对称图形,不符合题意;
(2)不是轴对称图形,不符合题意;
(3)是轴对称图形,符合题意;
(4)是轴对称图形,符合题意;
故答案为:(3)(4).
12.【解答】解:∵DE是△ABC中的边AC上的垂直平分线,
∴AD=CD,
∵AB=5cm,BC=8cm,
∴△ABD的周长为:AB+BD+AD=AB+BD+CD=AB+BC=13(cm).
故答案是:13.
13.【解答】解:∵DE是AC的垂直平分线,
∴DA=DC.
∵AB=5cm,BC=12cm,
∴△ABD的周长=AB+BD+DA=AB+BD+DC=AB+BC=17cm,
故答案为:17.
14.【解答】解:∵DE,FG分别是△ABC的AB,AC边的垂直平分线,
∴AE=BE,CG=AG,
∵BC=12,GE=2,
∴AE+AG=BE+CG=12+2=14,
∴△AGE的周长是AG+AE+EG=14+2=16,
15.【解答】解:过点B作BE⊥AD,交AD的延长线于点E,连接AC′,则∠E=90°,
∵C、C'关于直线AB对称,
∴△ABC≌△ABC′,
∴AC=AC′=4,BC=BC′=8,∠BCA=∠BC′A=90°=∠E,
易证ACBE是矩形,
∴BE=AC=4,
∵∠BDE=∠ADC′
∴△BDE≌△ADC′(AAS),
∴BD=AD,
设BD=x,则DE=8﹣x,
在Rt△BDE中,由勾股定理得:x2=(8﹣x)2+42,
解得:x=5,即:AD=BD=5,
在Rt△ABC中,AB=,
△ABD的周长是:10+,
故答案为:10+.
三.解答题(共4小题)
16.【解答】解:∵DE垂直平分AB,
∴AE=BE,
∴∠B=∠EAB,
∵∠C=90°,∠CAE=∠B+36°,
∴∠B+36°+∠B+∠B=90°,
∴∠B=18°,
∴∠AEB=180°﹣18°﹣18°=144°.
17.【解答】解:(1)∵AD垂直平分BE,EF垂直平分AC,
∴AB=AE=EC,
∴∠C=∠CAE,
∵∠BAE=40°,
∴∠AED=70°,
∴∠C=∠AED=35°;
(2)∵△ABC周长14cm,AC=6cm,
∴AB+BE+EC=8cm,
即2DE+2EC=8cm,
∴DE+EC=DC=4cm.
18.【解答】解:(1)∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=38°,
∵AB=AC,
∴∠ABC=∠C==71°,
∴∠EBC=∠ABC﹣∠ABE=71°﹣38°=33°;
(2)当BC=13cm时,AB=AC=11.5cm,
∵AB>BC,
∴此时不符合题意;舍去,
∵AE=BE,
当AB=AC=13cm时,则BC=10cm,
∵AE=BE,
∴△BCE的周长为BC+BE+CE=BC+AE+CE=BC+AC=10cm+13cm=23cm;
即△BCE的周长为23cm.
19.【解答】解:(1)设∠ADC=x,∠BEC=y.
∵AF垂直平分CD,
∴AC=AD,
∴∠ADC=∠ACD=x,
同理∠BEC=∠BCE=y.
在△ACD中,∵∠ADC+∠ACD+∠CAD=180°,
∴2x+∠CAD=180°①,
同理,2y+∠CBE=180°②,
①+②,得2x+2y+∠CAD+∠CBE=360°③,
∵∠CAD+∠CBE+∠ACB=180°,∠ACB=90°,
∴∠CAD+∠CBE=90°④,
④代入③,得2x+2y+90°=360°,
∴x+y=135°,
∴∠ECD=180°﹣(x+y)=45°;
(2)由(1)可得2x+2y+∠CAD+∠CBE=360°,
∵∠CAD+∠CBE=180°﹣∠ACB=180°﹣α,
∴2x+2y+180°﹣α=360°,
∴x+y=90°+α,
∴∠ECD=180°﹣(x+y)=180°﹣(90°+α)=90°﹣α.
一.选择题
1.我国民间,流传着许多含有吉祥意义的图案,表示对幸福生活的向往,良辰佳节的祝贺.比如下列图案分别表示“福”“禄”“寿”“喜”,其中是轴对称图形的有几个( )
A.1个 B.2个 C.3个 D.4个
2.如图,设L1和L2是镜面平行相对且间距为30cm的两面镜子,把一个小球A放在L1和L2之间,小球在镜L1中的像为A′,A′在镜L2中的像为A′′,则AA′′等于( )
A.10cm B.20cm C.40cm D.60cm
3.如图,从标有数字1,2,3,4的四个小正方形中拿走一个,成为一个轴对称图形,则应该拿走的小正方形的标号是( )
A.1 B.2 C.3 D.4
4.如图,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于点F,若∠FAC=65°,则∠B的度数为( )
A.45° B.50° C.65° D.60°
5.如图,不是轴对称图形的是( )
A. B.
C. D.
6.如图,在△ABC中,BC的垂直平分线分别交AC,BC于点D,E.若△ABC的周长为16,BE=3,则△ABD的周长为( )
A.6 B.8 C.12 D.10
7.如图,点D,E分别在△ABC的边AC、BC上,∠ABD:∠A:∠C=2:6:5,若DE垂直平分BC,则∠BDE=( )
A.30° B.35° C.40° D.50°
8.在正方形网格中,△ABC的位置如图所示,且顶点在格点上,在△ABC内部有E、F、G、H四个格点,到△ABC三个顶点距离相等的点是( )
A.点E B.点F C.点G D.点H
9.下列图形中,对称轴的条数为2的倍数的是( )
A. B.
C. D.
10.在平面内,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形( )
A.三条角平分线的交点
B.三条高线的交点
C.三条中线的交点
D.三条边垂直平分线的交点
二.填空题
11.如图所示的4组图形中,左右两个图形成轴对称的是第 组.
12.如图,DE是△ABC的边AC上的垂直平分线,AB=5cm,BC=8cm,则△ABD的周长为 cm.
13.如图,在△ABC中,DE是AC的垂直平分线,AB=5cm,BC=12cm,则△ABD的周长为 cm.
14.如图所示,DE、FG分别是△ABC两边AB、AC的中垂线,分别交BC于E、G.若BC=12,EG=2,则△AEG的周长是 .
15.如图,在Rt△ABC中,∠ACB=90°,作C点关于直线AB的对称点C',连接BC'.过A点作DA⊥AC交BC'于点D,若AC=4cm,BC=8cm,则△ABD的周长是 cm.
三.解答题
16.如图,在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB,BC于点D,E,若∠CAE=∠B+36°,求∠AEB的度数.
17.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
(1)若∠BAE=40°,求∠C的度数;
(2)若△ABC周长为14cm,AC=6cm,求DC长.
18.在△ABC中,AB>BC,AB=AC,DE是AB的垂直平分线,垂足为D点,交AC于点E.
(1)若∠ABE=38°,求∠EBC的度数;
(2)若△ABC的周长为36cm,一边为13cm,求△BCE的周长.
19.如图,在△ABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE
(1)求∠ECD的度数;
(2)若∠ACB为α,则∠ECD的度数能否用含α的式子来表示.
参考答案与试题解析
一.选择题
1.【解答】解:第一个图形不是轴对称图形,
第二、三、四个图形是轴对称图形,
共3个轴对称图形,
故选:C.
2.【解答】解:如图所示,经过反射后,A'B=AB,A'C=CA'',
∴AA''=AC+A''C=AC+A'C=AC+2AB+AC=2BC=60cm.
故选:D.
3.【解答】解:从标有数字1,2,3,4的四个小正方形中拿走2,就可以成为一个轴对称图形.
故选:B.
4.【解答】解:∵AD是∠BAC的平分线,
∴∠CAD=∠BAD,
∵EF垂直平分AD,
∴FA=FD,
∴∠FDA=∠FAD=∠FAC+∠CAD,
∵∠FDA是△ABD的一个外角,
∴∠B=∠FDA﹣∠BAD=∠FDA﹣∠CAD=65°,
故选:C.
5.【解答】解:A、不是轴对称图形;
B、是轴对称图形;
C、是轴对称图形;
D、是轴对称图形;
故选:A.
6.【解答】解:∵DE是BC的垂直平分线,
∴DB=DC,BC=2BE=6,
∵△ABC的周长为16,
∴AB+BC+AC=16,
∴AB+AC=10,
∴△ABD的周长=AB+AD+BD=AB+AD+DC=AB+AC=10,
故选:D.
7.【解答】解:∵∠ABD:∠A:∠C=2:6:5,
∴设∠ABD=2k,∠A=6k,∠C=5k,
∵DE垂直平分BC,
∴BD=CD,
∴∠DBC=∠C=5k,
∴∠ABC=7k,
∵∠A+∠ABC+∠C=180°,
∴6k+7k+5k=180°,
∴k=10°,
∴∠DBE=50°,
∵∠DEB=90°,
∴∠BDE=40°,
故选:C.
8.【解答】解:∵BF=AF=CF==,
∴到△ABC三个顶点距离相等的点是F,
故选:B.
9.【解答】解:A、图形有一条对称轴,不符合题意;
B、图形有三条对称轴,不符合题意;
C、图形有四条对称轴,符合题意;
D、图形有一条对称轴,不符合题意;
故选:C.
10.【解答】解:∵点到三角形三个顶点的距离相等,
∴这个点一定是三角形三条边的垂直平分线的交点,
故选:D.
二.填空题(共5小题)
11.【解答】解:(1)不是轴对称图形,不符合题意;
(2)不是轴对称图形,不符合题意;
(3)是轴对称图形,符合题意;
(4)是轴对称图形,符合题意;
故答案为:(3)(4).
12.【解答】解:∵DE是△ABC中的边AC上的垂直平分线,
∴AD=CD,
∵AB=5cm,BC=8cm,
∴△ABD的周长为:AB+BD+AD=AB+BD+CD=AB+BC=13(cm).
故答案是:13.
13.【解答】解:∵DE是AC的垂直平分线,
∴DA=DC.
∵AB=5cm,BC=12cm,
∴△ABD的周长=AB+BD+DA=AB+BD+DC=AB+BC=17cm,
故答案为:17.
14.【解答】解:∵DE,FG分别是△ABC的AB,AC边的垂直平分线,
∴AE=BE,CG=AG,
∵BC=12,GE=2,
∴AE+AG=BE+CG=12+2=14,
∴△AGE的周长是AG+AE+EG=14+2=16,
15.【解答】解:过点B作BE⊥AD,交AD的延长线于点E,连接AC′,则∠E=90°,
∵C、C'关于直线AB对称,
∴△ABC≌△ABC′,
∴AC=AC′=4,BC=BC′=8,∠BCA=∠BC′A=90°=∠E,
易证ACBE是矩形,
∴BE=AC=4,
∵∠BDE=∠ADC′
∴△BDE≌△ADC′(AAS),
∴BD=AD,
设BD=x,则DE=8﹣x,
在Rt△BDE中,由勾股定理得:x2=(8﹣x)2+42,
解得:x=5,即:AD=BD=5,
在Rt△ABC中,AB=,
△ABD的周长是:10+,
故答案为:10+.
三.解答题(共4小题)
16.【解答】解:∵DE垂直平分AB,
∴AE=BE,
∴∠B=∠EAB,
∵∠C=90°,∠CAE=∠B+36°,
∴∠B+36°+∠B+∠B=90°,
∴∠B=18°,
∴∠AEB=180°﹣18°﹣18°=144°.
17.【解答】解:(1)∵AD垂直平分BE,EF垂直平分AC,
∴AB=AE=EC,
∴∠C=∠CAE,
∵∠BAE=40°,
∴∠AED=70°,
∴∠C=∠AED=35°;
(2)∵△ABC周长14cm,AC=6cm,
∴AB+BE+EC=8cm,
即2DE+2EC=8cm,
∴DE+EC=DC=4cm.
18.【解答】解:(1)∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=38°,
∵AB=AC,
∴∠ABC=∠C==71°,
∴∠EBC=∠ABC﹣∠ABE=71°﹣38°=33°;
(2)当BC=13cm时,AB=AC=11.5cm,
∵AB>BC,
∴此时不符合题意;舍去,
∵AE=BE,
当AB=AC=13cm时,则BC=10cm,
∵AE=BE,
∴△BCE的周长为BC+BE+CE=BC+AE+CE=BC+AC=10cm+13cm=23cm;
即△BCE的周长为23cm.
19.【解答】解:(1)设∠ADC=x,∠BEC=y.
∵AF垂直平分CD,
∴AC=AD,
∴∠ADC=∠ACD=x,
同理∠BEC=∠BCE=y.
在△ACD中,∵∠ADC+∠ACD+∠CAD=180°,
∴2x+∠CAD=180°①,
同理,2y+∠CBE=180°②,
①+②,得2x+2y+∠CAD+∠CBE=360°③,
∵∠CAD+∠CBE+∠ACB=180°,∠ACB=90°,
∴∠CAD+∠CBE=90°④,
④代入③,得2x+2y+90°=360°,
∴x+y=135°,
∴∠ECD=180°﹣(x+y)=45°;
(2)由(1)可得2x+2y+∠CAD+∠CBE=360°,
∵∠CAD+∠CBE=180°﹣∠ACB=180°﹣α,
∴2x+2y+180°﹣α=360°,
∴x+y=90°+α,
∴∠ECD=180°﹣(x+y)=180°﹣(90°+α)=90°﹣α.
