2020年人教版小学数学六年级上册第八单元质量检测卷(含答案)
文档属性
| 名称 | 2020年人教版小学数学六年级上册第八单元质量检测卷(含答案) | 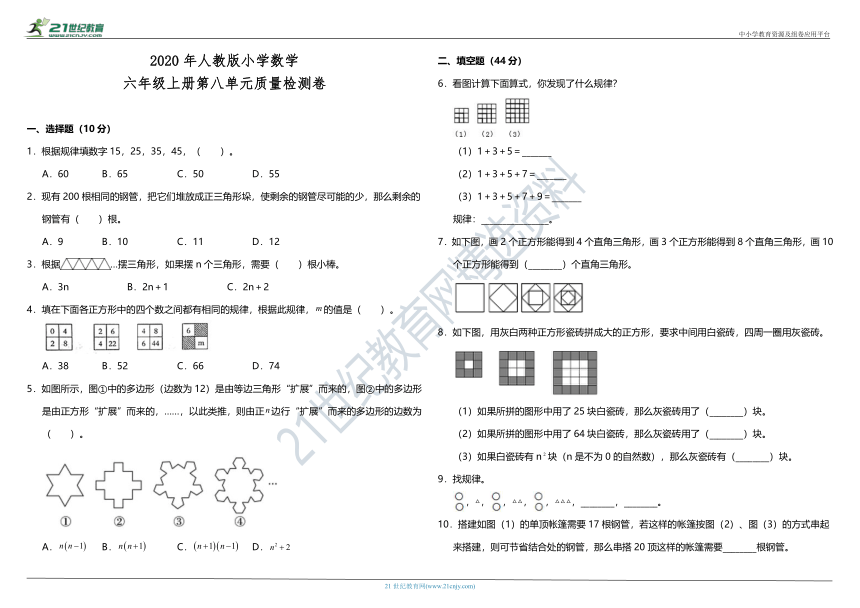 | |
| 格式 | doc | ||
| 文件大小 | 428.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 22:26:33 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2020年人教版小学数学
六年级上册第八单元质量检测卷
一、选择题(10分)
1.根据规律填数字15,25,35,45,( )。
A.60 B.65 C.50 D.55
2.现有200根相同的钢管,把它们堆放成正三角形垛,使剩余的钢管尽可能的少,那么剩余的 钢管有( )根。
A.9 B.10 C.11 D.12
3.根据…摆三角形,如果摆n个三角形,需要( )根小棒。
A.3n B.2n+1 C.2n+2
4.填在下面各正方形中的四个数之间都有相同的规律,根据此规律,的值是( )。
A.38 B.52 C.66 D.74
5.如图所示,图①中的多边形(边数为12)是由等边三角形“扩展”而来的,图②中的多边形 是由正方形“扩展”而来的,……,以此类推,则由正边行“扩展”而来的多边形的边数为 ( )。
A. B. C. D.
二、填空题(44分)
6.看图计算下面算式,你发现了什么规律?
(1)1+3+5=_______
(2)1+3+5+7=_______
(3)1+3+5+7+9=_______
规律:________________。
7.如下图,画2个正方形能得到4个直角三角形,画3个正方形能得到8个直角三角形,画10 个正方形能得到(________)个直角三角形。
8.如下图,用灰白两种正方形瓷砖拼成大的正方形,要求中间用白瓷砖,四周一圈用灰瓷砖。
(1)如果所拼的图形中用了25块白瓷砖,那么灰瓷砖用了(________)块。
(2)如果所拼的图形中用了64块白瓷砖,那么灰瓷砖用了(________)块。
(3)如果白瓷砖有n块(n是不为0的自然数),那么灰瓷砖有(________)块。
9.找规律。
,△,,△△,,△△△,________,________。
10.搭建如图(1)的单顶帐篷需要17根钢管,若这样的帐篷按图(2)、图(3)的方式串起 来搭建,则可节省结合处的钢管,那么串搭20顶这样的帐篷需要________根钢管。
11.1+3+5+7+9+11+13+11+9+7+5+3+1=(________)2+(________)2=(________)。
12.如图,一张桌子可坐4人,两张桌子可坐6人。像这样(________)张桌子拼起来可坐40 人。
13.仔细研究下图表示数的方法。
表示1;表示2;表示3;
表示4;表示5。
根据上图回答:
(1)表示________。
(2)表示________。
14.按这样的方式摆下去,摆4个连着的正六边形需要________根小棒,摆个连着的正六边形 需要________根小棒。
……
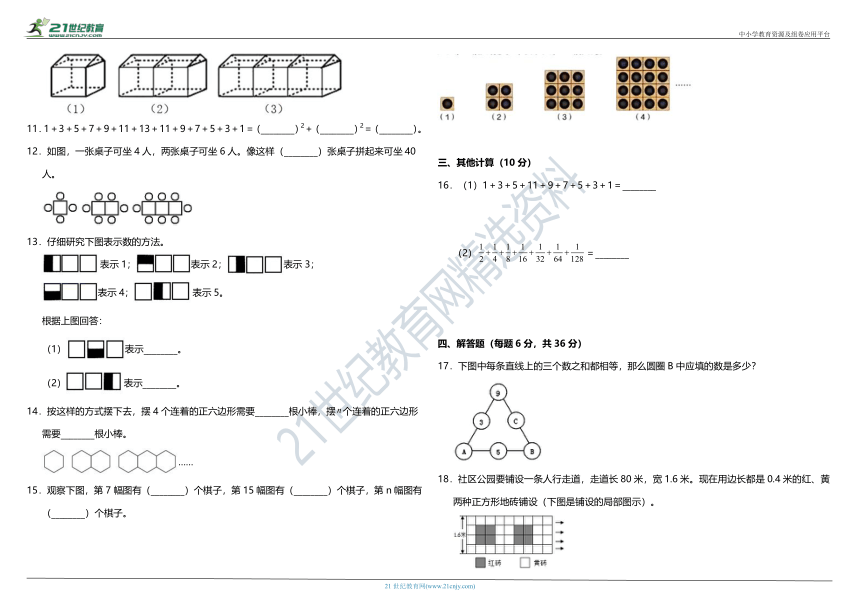
15.观察下图,第7幅图有(________)个棋子,第15幅图有(________)个棋子,第n幅图有 (________)个棋子。
三、其他计算(10分)
16.(1)1+3+5+11+9+7+5+3+1=________
(2)=________
四、解答题(每题6分,共36分)
17.下图中每条直线上的三个数之和都相等,那么圆圈B中应填的数是多少?
18.社区公园要铺设一条人行走道,走道长80米,宽1.6米。现在用边长都是0.4米的红、黄 两种正方形地砖铺设(下图是铺设的局部图示)。
(1)铺设这条人行走道一共需要多少块地砖?(不计损耗)
(2)铺设这条人行走道一共需要多少块红色地砖?(不计损耗)
19.请数一数下面各图中分别有多少个角?
( )个 ( )个
( )个 ( )个
(1)你发现图中边的数量与角的数量有什么关系吗?
(2)像上面这样的图中,如果有7条边,那么一共有多少个角?
(3)像上面这样的图中,如果有n条边,那么一共有多少个角?
20.用同样的小棒搭成以下图案。
需要4+3×1=7根小棒;
需要4+3×2=10根小棒;
需要4+3×3=13根小棒
照这样算:
(1)搭同样的10个正方形需要小棒多少根?
(2)现有46根小棒可以搭多少个正方形?
21.如图,将一张正方形纸片剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去.
(1)填表:
剪的次数 1 2 3 4 5
正方形个数
(2)如果剪了20次,共剪出多少个小正方形?
(3)观察图形,你还能发现什么规律?
观察表中三角形个数的变化规律。
图形
横截线条数 0 1
三角形个数 6
22.若三角形中横截线条数有0条,则有6个三角形;如果三角形中横截线条数有1条,则有(________)个三角形;三角形中横截线条数有2条,则有(________)个三角形;三角形中横截线条数有4条,则有(________)个三角形。
23.如果三角形中横截线条数有n条,则有(________)个三角形。(用含n的代数式来表示)
24.如果三角形中横截线条数有19条,则有多少个三角形?
参考答案
1.D
2.B
3.B
4.D
5.B
6.9,即32 16,即42; 25,即52 从1开始的连续几个奇数相加,即数的个数的平方
7.36
8.24 36 4n+4
9. △△△△
10.226
11.7 6 85
12.19张
13.8 9
14.21 5n+1
15.49 225 n2
16.45
17.7
18.(1)800块
(2)200块
19.1,3
6,10
(1)1+2+3+…+(边的数量-1)=角的数量
(2)1+2+3+…+6=21(个)
(3)[1+2+3+…+(n-1)]个
20.(1)31根 (2)15个
21.(1)4 7 10 13 16
(2)61
(3)每剪一次会比上一次多3个正方形,如果剪n次,正方形的个数为3n+1。
22. 12 18 30
23. (n+1)×6
24. 120
_21?????????è?????(www.21cnjy.com)_
2020年人教版小学数学
六年级上册第八单元质量检测卷
一、选择题(10分)
1.根据规律填数字15,25,35,45,( )。
A.60 B.65 C.50 D.55
2.现有200根相同的钢管,把它们堆放成正三角形垛,使剩余的钢管尽可能的少,那么剩余的 钢管有( )根。
A.9 B.10 C.11 D.12
3.根据…摆三角形,如果摆n个三角形,需要( )根小棒。
A.3n B.2n+1 C.2n+2
4.填在下面各正方形中的四个数之间都有相同的规律,根据此规律,的值是( )。
A.38 B.52 C.66 D.74
5.如图所示,图①中的多边形(边数为12)是由等边三角形“扩展”而来的,图②中的多边形 是由正方形“扩展”而来的,……,以此类推,则由正边行“扩展”而来的多边形的边数为 ( )。
A. B. C. D.
二、填空题(44分)
6.看图计算下面算式,你发现了什么规律?
(1)1+3+5=_______
(2)1+3+5+7=_______
(3)1+3+5+7+9=_______
规律:________________。
7.如下图,画2个正方形能得到4个直角三角形,画3个正方形能得到8个直角三角形,画10 个正方形能得到(________)个直角三角形。
8.如下图,用灰白两种正方形瓷砖拼成大的正方形,要求中间用白瓷砖,四周一圈用灰瓷砖。
(1)如果所拼的图形中用了25块白瓷砖,那么灰瓷砖用了(________)块。
(2)如果所拼的图形中用了64块白瓷砖,那么灰瓷砖用了(________)块。
(3)如果白瓷砖有n块(n是不为0的自然数),那么灰瓷砖有(________)块。
9.找规律。
,△,,△△,,△△△,________,________。
10.搭建如图(1)的单顶帐篷需要17根钢管,若这样的帐篷按图(2)、图(3)的方式串起 来搭建,则可节省结合处的钢管,那么串搭20顶这样的帐篷需要________根钢管。
11.1+3+5+7+9+11+13+11+9+7+5+3+1=(________)2+(________)2=(________)。
12.如图,一张桌子可坐4人,两张桌子可坐6人。像这样(________)张桌子拼起来可坐40 人。
13.仔细研究下图表示数的方法。
表示1;表示2;表示3;
表示4;表示5。
根据上图回答:
(1)表示________。
(2)表示________。
14.按这样的方式摆下去,摆4个连着的正六边形需要________根小棒,摆个连着的正六边形 需要________根小棒。
……
15.观察下图,第7幅图有(________)个棋子,第15幅图有(________)个棋子,第n幅图有 (________)个棋子。
三、其他计算(10分)
16.(1)1+3+5+11+9+7+5+3+1=________
(2)=________
四、解答题(每题6分,共36分)
17.下图中每条直线上的三个数之和都相等,那么圆圈B中应填的数是多少?
18.社区公园要铺设一条人行走道,走道长80米,宽1.6米。现在用边长都是0.4米的红、黄 两种正方形地砖铺设(下图是铺设的局部图示)。
(1)铺设这条人行走道一共需要多少块地砖?(不计损耗)
(2)铺设这条人行走道一共需要多少块红色地砖?(不计损耗)
19.请数一数下面各图中分别有多少个角?
( )个 ( )个
( )个 ( )个
(1)你发现图中边的数量与角的数量有什么关系吗?
(2)像上面这样的图中,如果有7条边,那么一共有多少个角?
(3)像上面这样的图中,如果有n条边,那么一共有多少个角?
20.用同样的小棒搭成以下图案。
需要4+3×1=7根小棒;
需要4+3×2=10根小棒;
需要4+3×3=13根小棒
照这样算:
(1)搭同样的10个正方形需要小棒多少根?
(2)现有46根小棒可以搭多少个正方形?
21.如图,将一张正方形纸片剪成四个大小形状一样的小正方形,然后将其中的一个小正方形再按同样的方法剪成四个小正方形,再将其中的一个小正方形剪成四个小正方形,如此循环进行下去.
(1)填表:
剪的次数 1 2 3 4 5
正方形个数
(2)如果剪了20次,共剪出多少个小正方形?
(3)观察图形,你还能发现什么规律?
观察表中三角形个数的变化规律。
图形
横截线条数 0 1
三角形个数 6
22.若三角形中横截线条数有0条,则有6个三角形;如果三角形中横截线条数有1条,则有(________)个三角形;三角形中横截线条数有2条,则有(________)个三角形;三角形中横截线条数有4条,则有(________)个三角形。
23.如果三角形中横截线条数有n条,则有(________)个三角形。(用含n的代数式来表示)
24.如果三角形中横截线条数有19条,则有多少个三角形?
参考答案
1.D
2.B
3.B
4.D
5.B
6.9,即32 16,即42; 25,即52 从1开始的连续几个奇数相加,即数的个数的平方
7.36
8.24 36 4n+4
9. △△△△
10.226
11.7 6 85
12.19张
13.8 9
14.21 5n+1
15.49 225 n2
16.45
17.7
18.(1)800块
(2)200块
19.1,3
6,10
(1)1+2+3+…+(边的数量-1)=角的数量
(2)1+2+3+…+6=21(个)
(3)[1+2+3+…+(n-1)]个
20.(1)31根 (2)15个
21.(1)4 7 10 13 16
(2)61
(3)每剪一次会比上一次多3个正方形,如果剪n次,正方形的个数为3n+1。
22. 12 18 30
23. (n+1)×6
24. 120
_21?????????è?????(www.21cnjy.com)_
