人教版九年级数学下册 27.3 位似 同步测试题(word版有答案)
文档属性
| 名称 | 人教版九年级数学下册 27.3 位似 同步测试题(word版有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 561.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 11:31:26 | ||
图片预览


文档简介
104902001069340012319000027.3 位似 同步测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 将△OAB以点O为位似中心放大为原来的2倍,得到△OA'B',则S△OAB:S△OA'B'等于( )
A.1:2 B.1:3 C.1:4 D.1:8
?
2. 如图,已知 △OAB与△OA'B' 是相似比为1:2的位似图形,点O是位似中心,若△OAB内一点P(x,y)与△OA'B'内一点P'是一对对应点,则点P'的坐标是(? ? ? ? ?)
A.(2x,2y)? B.(-2x,-2y) C.(12x,12y) D.?(-12x,-12y)
?
3. 在平面直角坐标系中,点A6,3,以原点O为位似中心,在第一象限内把线段OA缩小为原来的13得到线段OC,则点C的坐标为(? ? ? ? )
A.2,1 B.2,0 C.3,3 D.3,1
?
4. 下列语句正确的是( )
A.相似图形一定是位似图形,位似图形一定是相似图形
B.位似图形一定是相似图形,而且位似比等于相似比
C.利用位似变换只能放大图形,不能缩小图形
D.利用位似变换只能缩小图形,不能放大图形
?
5. 在平面直角坐标系xOy中,点A-6,2,B-4,4 ,将△ABO以原点O为位似中心,相似比为2:1,进行位似变换,则点A的对应点A'的坐标是(? ? ? ? )
A.-3,1 或-2,-2 B.-3,1或 3,-1
C.-12,4或12,-4 D.-12,4 或 -8,-8
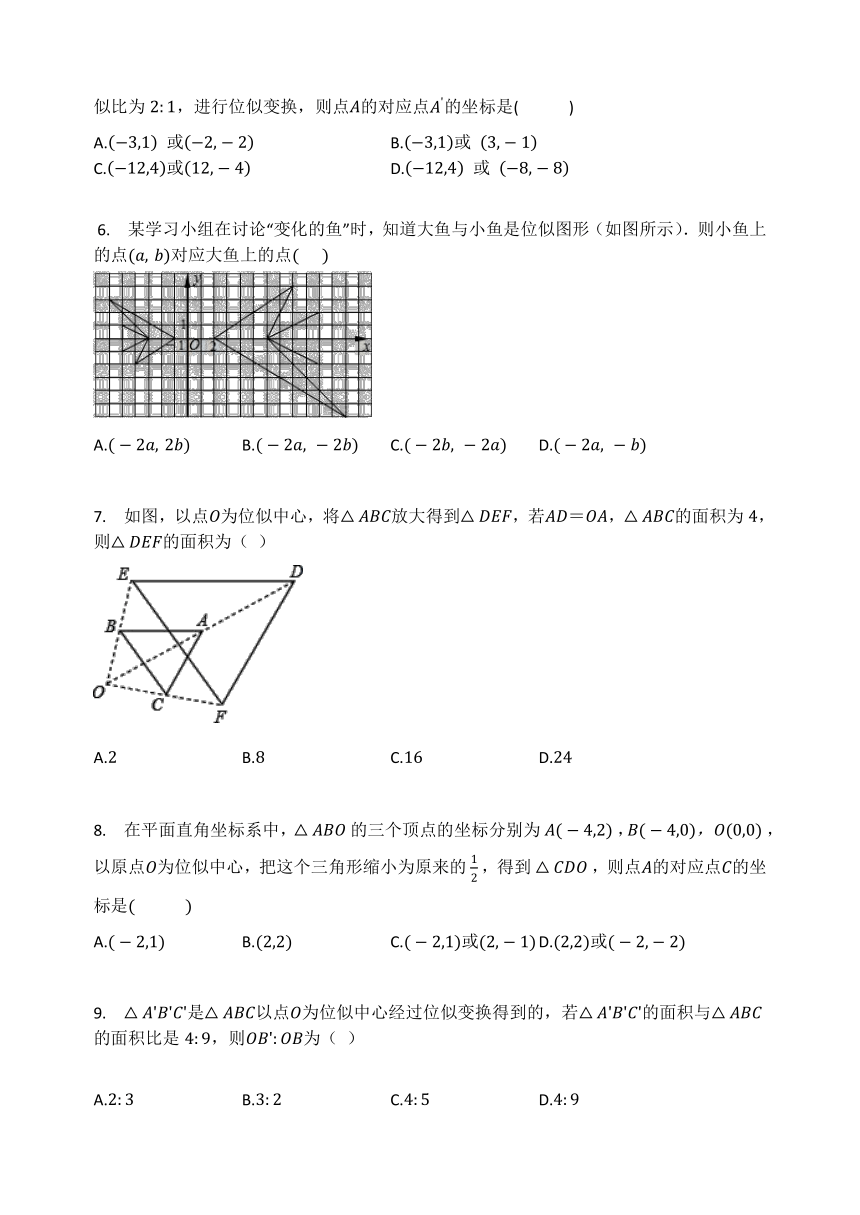
?6. 某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图所示).则小鱼上的点(a,?b)对应大鱼上的点(????????)
A.(-2a,?2b) B.(-2a,?-2b) C.(-2b,?-2a) D.(-2a,?-b)
?
7. 如图,以点O为位似中心,将△ABC放大得到△DEF,若AD=OA,△ABC的面积为4,则△DEF的面积为( )
A.2 B.8 C.16 D.24
?
8. 在平面直角坐标系中,?△ABO?的三个顶点的坐标分别为?A(-4,2)?,B(-4,0),O(0,0)?,以原点O为位似中心,把这个三角形缩小为原来的?12?,得到?△CDO?,则点A的对应点C的坐标是(? ? ? ? )
A.(-2,1) B.(2,2) C.(-2,1)或(2,-1) D.(2,2)或(-2,-2)
?
9. △A'B'C'是△ABC以点O为位似中心经过位似变换得到的,若△A'B'C'的面积与△ABC的面积比是4:9,则OB':OB为( )
A.2:3 B.3:2 C.4:5 D.4:9
?
10. 如图,将△DEF缩小为原来的一半,操作方法如下:任意取一点P,连接DP,取DP的中点A,再连接EP、FP,取它们的中点B、C,得到△ABC,则下列说法正确的有( )
①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比是1:2;④△ABC与△DEF的面积比是1:2.
A.1个 B.2个 C.3个 D.4个
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , )
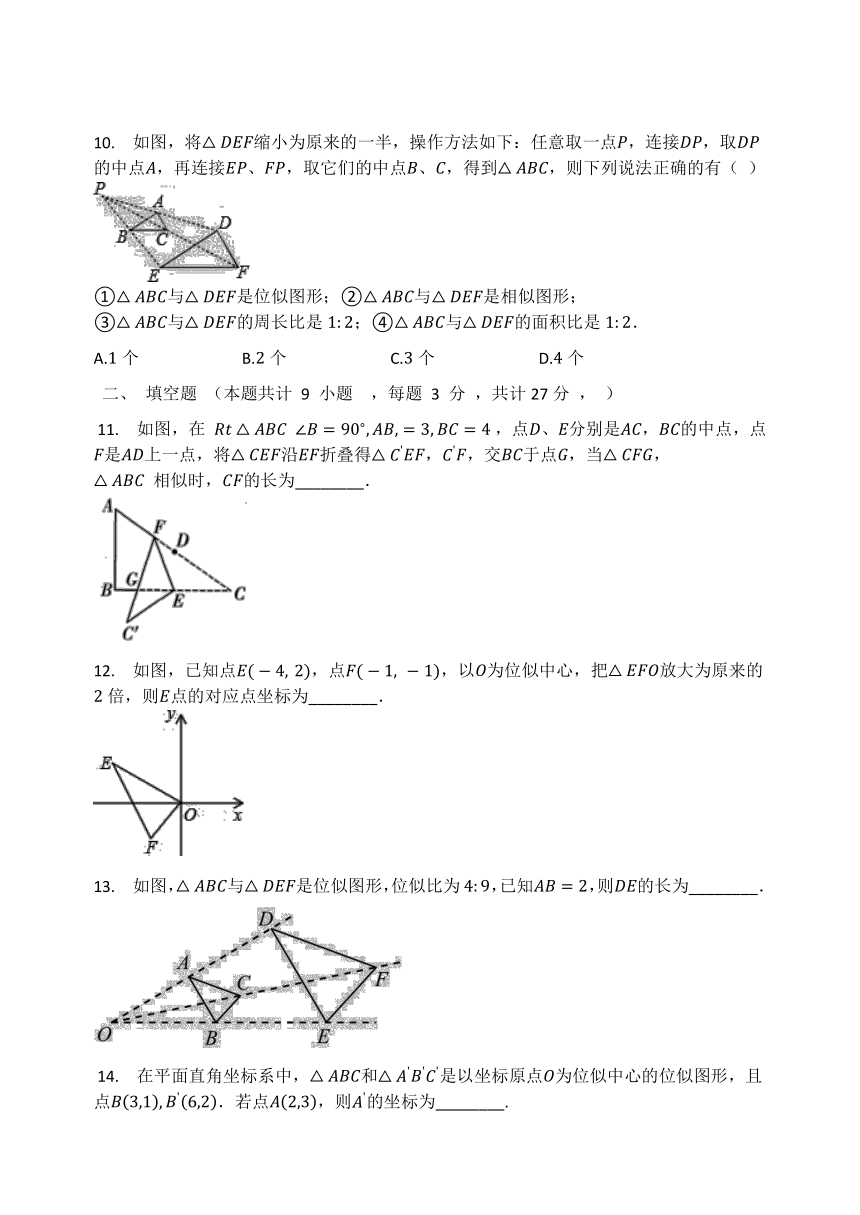
?11. 如图,在 Rt△ABC ∠B=90?,AB,=3,BC=4?,点D、E分别是AC,BC的中点,点F是AD上一点,将△CEF沿EF折叠得△C'EF,C'F,交BC于点G,当△CFG,
△ABC 相似时,CF的长为________.
?
12. 如图,已知点E(-4,?2),点F(-1,?-1),以O为位似中心,把△EFO放大为原来的2倍,则E点的对应点坐标为________.
? ?
13. 如图,△ABC与△DEF是位似图形,位似比为4:9,已知AB=2,则DE的长为________.
?14. 在平面直角坐标系中,△ABC和△A'B'C'是以坐标原点O为位似中心的位似图形,且点B3,1,B'6,2.若点A2,3,则A'的坐标为________.
?
15. 已知△ABC,以点A为位似中心,作出△ADE,使△ADE是△ABC放大2倍的图形,这样的图形可以作出________个.他们之间的关系是________.
?
16. 如图,在平面直角坐标系中,△ABO三个顶点的坐标分别为A(-2,?4),B(-4,?0),O(0,?0).以原点O为位似中心,把这个三角形缩小为原来的12,得到△CDO,则点A的对应点C的坐标是________.
?
17. 如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,AB=4,则A1B1的长为________.
?
18. 在△ABC中,AB=BC,∠B=90?,将△ABC沿BC方向平移,得到△A'CC',以C为位似中心,作△DEC?与△ABC位似,位似比为1:2,F为CC'的中点,连接DF, A'F ,则A'FDF的值为________.
?
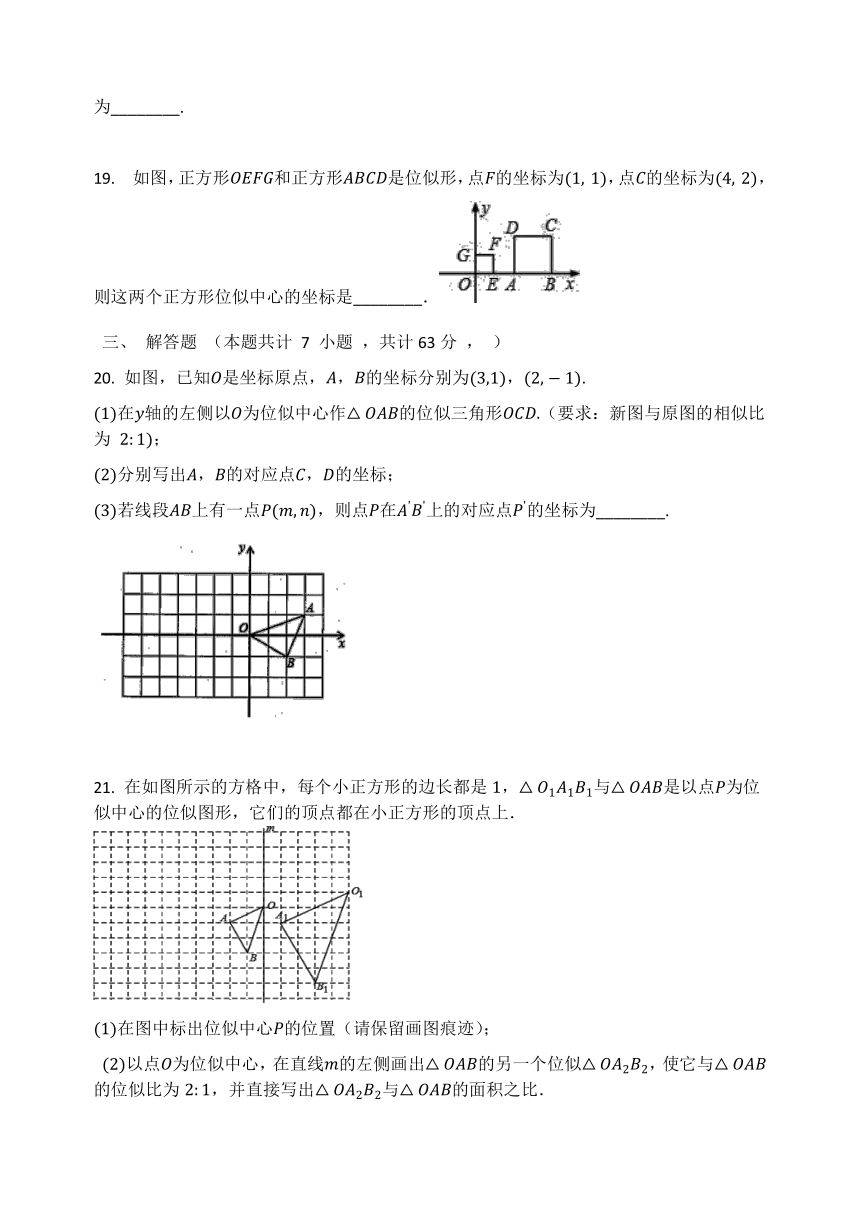
19. 如图,正方形OEFG和正方形ABCD是位似形,点F的坐标为(1,?1),点C的坐标为(4,?2),则这两个正方形位似中心的坐标是________.
三、 解答题 (本题共计 7 小题 ,共计63分 , ) ?
20. 如图,已知O是坐标原点,A,B的坐标分别为(3,1),(2,-1).
(1)在y轴的左侧以O为位似中心作△OAB的位似三角形OCD.(要求:新图与原图的相似比为 2:1);
(2)分别写出A,B的对应点C,D的坐标;
(3)若线段AB上有一点P(m,n),则点P在A'B'上的对应点P'的坐标为________.
?
21. 在如图所示的方格中,每个小正方形的边长都是1,△O1A1B1与△OAB是以点P为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)在图中标出位似中心P的位置(请保留画图痕迹);
(2)以点O为位似中心,在直线m的左侧画出△OAB的另一个位似△OA2B2,使它与△OAB的位似比为2:1,并直接写出△OA2B2与△OAB的面积之比.
?
22. 如图,已知O是坐标原点,B、C两点的坐标分别为(3,?-1)、(2,?1).
1以O点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
2分别写出B、C两点的对应点B'、C'的坐标.
?
23. 如图示,在边长为1的正方形网格中,建立如下平面直角坐标系中,其中△ABO的顶点A(3,4),B(8,1),O(0,0).
1以O为位似中心,在第一象限内作出△ABO的位似图形△A1B1O,其相似比为12.
2将△ABO绕点O逆时针旋转90?得到△A2B2O.
?
24. 如图,已知O是原点,B、C两点的坐标分别为(3,?-1),(2,?1).
(1)以点O为位似中心,在y轴的左侧将△OBC扩大为原来的两倍(即新图与原图的相似比为2),画出图形并写出点B,C的对应点的坐标;
(2)如果△OBC内部一点M的坐标为(a,?b),写出点M的对应点M'的坐标.
?
25. 在放映电影时,我们需要把胶片上的图片放大到银幕上,以便人们欣赏.如图,点P为放映机的光源,△ABC是胶片上面的画面,△A'B'C'为银幕上看到的画面.若胶片上图片的规格是2.5cm×2.5cm,放映的银幕规格是2m×2m,光源P与胶片的距离是20cm,则银幕应距离光源P多远时,放映的图象正好布满整个银幕?
?
26. 如图,已知O是坐标原点,A、B的坐标分别为(3,?1)、(2,?-1).
(1)在y轴的左侧以O为位似中心作△OAB的位似三角形OCD,使新图与原图的相似比为2:1;
(2)分别写出A,B的对应点C、D的坐标;
(3)求△OCD的面积.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
∵ 将△OAB以点O为位似中心放大为原来的2倍,得到△OA'B',
∴ △OAB与△OA'B'的位似比为1:2,
则S△OAB:S△OA'B'=1:4.
2.
【答案】
B
【解答】
解:∵ △OAB与△OA'B'是相似比为1:2的位似图形,
△OAB内一点P(x,y)与△OA'B'内一点P'是一对对应点,
∴ P'的坐标是(-2x,-2y).
故选B.
3.
【答案】
A
【解答】
解:在平面直角坐标系中,点A6,3,以原点O为位似中心,
在第一象限内把线段OA缩小为原来的13得到线段OC,
则点A的对应点C的坐标为(6×13,3×13),
即C点坐标为2,1.
故选A.
4.
【答案】
B
【解答】
解:A、相似图形对应点的连线不一定都经过同一点,所以不一定是位似图形,错误;
B、位似图形一定是相似图形,而且位似比等于相似比,正确;
C和D选项均利用位似变换能放大图形,也能缩小图形,错误;
故选B.
5.
【答案】
B
【解答】
解:△ABO的一个顶点A的坐标是-6,2,
以原点O为位似中心相似比为1:2,将△ABO缩小得到它的位似图形△A'B'O',
∴ 点A'的坐标是:-12×6,12×2?,-12×-6,-12×2,
即-3,1或?3,-1.
故选B.
6.
【答案】
B
【解答】
解:根据图形可得,两个图形的位似比是1:2,
∴ 对应点是(-2a,?-2b).
故选B.
7.
【答案】
C
【解答】
∵ 以点O为位似中心,将△ABC放大得到△DEF,AD=OA,
∴ OA:OD=1:2,
∴ △ABC与△DEF的面积之比为:1:4,
∵ △ABC的面积为4,
∴ △DEF的面积为:16.
8.
【答案】
C
【解答】
解:∵ 点A(-4,2),且相似比为12,
∴ 当△CDO与△ABO在y轴同侧时,点C的坐标为(-2,1),
当△CDO与△ABO在y轴异侧时,点C的坐标为(2,-1).
故选C.
9.
【答案】
A
【解答】
由位似变换的性质可知,A'B',A?CIIAC,
ΔA'BC'-△ABC
ΔA'BC与△ABC的面积的比4:9
∴ ΔA'B'C’与△ABC的相似比为2:3
∴ OB'OB=23
故选A.
10.
【答案】
C
【解答】
解:由于△ABC是由△DEF缩小一半得到,所以△ABC与△DEF是位似图形,①正确;
位似图形也是相似图形,②正确;
将△DEF缩小为原来的一半,得到△ABC,所以△ABC与△DEF的位似比为1:2,所以其周长比也为1:2,③正确;
所以其面积比为1:4,④错误.
题中共有3个结论正确.
故选C.
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
11.
【答案】
4或2.8
【解答】
解:
①当FG⊥BC时,
将△CEF沿EF折叠得△C'EF,
∴ ∠C'=∠C,C'E=CE=2,
∴ sin∠C=sin∠C',
∴ ABAC=EGC'E,
∴ EG=1.2,
∵ FG//AB,
∴ CGBC=CFAC, 即
3.24=CF5,
∴ CF=4;
②当 GF⊥AC 时,如图,
将 △CEF沿EF折叠得 △C'EF,
∴ ∠1=∠2=45?,
∴ HF=HE,
∵ sin∠C=sin∠C'=EHC'E=ABAC,
∴ EH=2×35=65,
∴ C'H=C?'E2-EH2=85,
∴ CF=C'F=C'H+HF=1.6+1.2=2.8.
综上所述,当 △CFG与△ABC相似时,CF的长为4或2.8.
故答案为∶4或2.8.
12.
【答案】
(-8,?4)或(8,?-4)
【解答】
解:根据题意可知,点E对应点的坐标是E(-4,?2)的坐标同时乘以2或-2,
所以对应点的坐标为(-8,?4)或(8,?-4).
故答案为:(-8,4)或(8,-4).
13.
【答案】
92
【解答】
解:∵ △ABC与△DEF是位似图形,位似比为4:9,
∴ AB:DE=4:9,
∴ DE=92.
故答案为:92.
14.
【答案】
4,6
【解答】
解:△ABC和△A'B'C'是以坐标原点O为位似中心的位似图形,且点B3,1,B'6,2,
则△ABC和△A'B'C'的相似比为1:2,
∵ A2,3,
∴ A'的坐标为2×2,3×2,即4,6.
故答案为:4,6.
15.
【答案】
2,成中心对称
【解答】
解:以点A为位似中心,作出△ADE,使△ADE是△ABC放大2倍的图形,
可作出两个位似图形,
由于其是关于同一个点的位似图形,所以其位似图形为关于点A成中心对称.
故答案为:2,成中心对称.
16.
【答案】
(-1,?2)或(1,?-2)
【解答】
解:以原点O为位似中心,把这个三角形缩小为原来的12,点A的坐标为(-2,?4),
∴ 点C的坐标为(-2×12,?4×12)或(2×12,?-4×12),即(-1,?2)或(1,?-2).
故答案为:(-1,?2)或(1,?-2).
17.
【答案】
2
【解答】
解:∵ △ABC和△A1B1C1是以点O为位似中心的位似三角形,C1为OC的中点,AB=4,
∴ A1B1=12AB=2.
故答案为:2.
18.
【答案】
1或5
【解答】
解:设AB=BC=2x,
①如图1,当点D在AC上时,
∵ △ABC?△A'CC',
∴ A'C=CC'=2x,
∵ F为 CC'?的中点,
∴ CF=x,
则A'F=A'C2+CF2=5x,
又∵ △DEC?△ABC,且DEAB=CECB=12,
∴ DE=CE=x,
则EF=2x,
∴ DF=DE2+EF2=5x,
∴ A'FDF=5x5x=1;
②如图2,当点D在AC延长线上时,
由①知A'F=A'C2+CF2=5x,
DF=DE=x,
∴ A'FDF=5xx=5.
故答案为:1或5.
19.
【答案】
(-2,?0)
【解答】
解:两个图形位似时,位似中心就是CF与x轴的交点,
设直线CF解析式为y=kx+b,将C(4,?2),F(1,?1)代入,得
4k+b=2k+b=1,解得k=13b=23,即y=13x+23,
令y=0得x=-2,
∴ O'坐标是(-2,?0).
故答案是(-2,?0)
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
20.
【答案】
解:(1)如图:△OCD即为所求.
(2)由图可知:C:-6,-2,D:-4,2.
-2m,-2n
【解答】
解:(1)如图:△OCD即为所求.
(2)由图可知:C:-6,-2,D:-4,2.
(3)根据原点位似的特点可知P'-2m,-2n.
故答案为:-2m,-2n.
21.
【答案】
解:(1)如图所示:点P即为所求.
(2)如图所示:
△OA2B2,即为所求.
△OA2B2与△OAB的面积之比是:4:1.
【解答】
解:(1)如图所示:点P即为所求.
(2)如图所示:
△OA2B2,即为所求.
△OA2B2与△OAB的面积之比是:4:1.
22.
【答案】
解:(1)△OB'C'是所求的三角形;
2B'的坐标是(-6,?2),C'的坐标是(-4,?-2).
【解答】
解:(1)△OB'C'是所求的三角形;
2B'的坐标是(-6,?2),C'的坐标是(-4,?-2).
23.
【答案】
解:1作出位似图形如图所示,△A1B1O即为所求.
2如图△A2B2O即为所求:
【解答】
解:1作出位似图形如图所示,△A1B1O即为所求.
2如图△A2B2O即为所求:
24.
【答案】
解:(1)如图,△OB1C1为所作,点B1,C1点的坐标分别为(-6,?2),(-4,?-2);
(2)把M点的横纵坐标分别乘以-2即可得到M1的坐标,
所以点M的对应点M'的坐标为(-2a,?-2b).
【解答】
解:(1)如图,△OB1C1为所作,点B1,C1点的坐标分别为(-6,?2),(-4,?-2);
(2)把M点的横纵坐标分别乘以-2即可得到M1的坐标,
所以点M的对应点M'的坐标为(-2a,?-2b).
25.
【答案】
解:图中△A'B'C'是△ABC的位似图形,
设银幕距离光源P为xm时,放映的图象正好布满整个银幕,
则位似比=x0.2=22.5×10-2,
解得x=16.
即银幕应距离光源P为16m时,放映的图象正好布满整个银幕.
【解答】
解:图中△A'B'C'是△ABC的位似图形,
设银幕距离光源P为xm时,放映的图象正好布满整个银幕,
则位似比=x0.2=22.5×10-2,
解得x=16.
即银幕应距离光源P为16m时,放映的图象正好布满整个银幕.
26.
【答案】
如图,△OCD即为所求.
C(-6,?-2),D(-4,?2),
S△OCD=24-12×4×2-12×6×2-12×2×4=10.
【解答】
如图,△OCD即为所求.
C(-6,?-2),D(-4,?2),
S△OCD=24-12×4×2-12×6×2-12×2×4=10.
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 将△OAB以点O为位似中心放大为原来的2倍,得到△OA'B',则S△OAB:S△OA'B'等于( )
A.1:2 B.1:3 C.1:4 D.1:8
?
2. 如图,已知 △OAB与△OA'B' 是相似比为1:2的位似图形,点O是位似中心,若△OAB内一点P(x,y)与△OA'B'内一点P'是一对对应点,则点P'的坐标是(? ? ? ? ?)
A.(2x,2y)? B.(-2x,-2y) C.(12x,12y) D.?(-12x,-12y)
?
3. 在平面直角坐标系中,点A6,3,以原点O为位似中心,在第一象限内把线段OA缩小为原来的13得到线段OC,则点C的坐标为(? ? ? ? )
A.2,1 B.2,0 C.3,3 D.3,1
?
4. 下列语句正确的是( )
A.相似图形一定是位似图形,位似图形一定是相似图形
B.位似图形一定是相似图形,而且位似比等于相似比
C.利用位似变换只能放大图形,不能缩小图形
D.利用位似变换只能缩小图形,不能放大图形
?
5. 在平面直角坐标系xOy中,点A-6,2,B-4,4 ,将△ABO以原点O为位似中心,相似比为2:1,进行位似变换,则点A的对应点A'的坐标是(? ? ? ? )
A.-3,1 或-2,-2 B.-3,1或 3,-1
C.-12,4或12,-4 D.-12,4 或 -8,-8
?6. 某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图所示).则小鱼上的点(a,?b)对应大鱼上的点(????????)
A.(-2a,?2b) B.(-2a,?-2b) C.(-2b,?-2a) D.(-2a,?-b)
?
7. 如图,以点O为位似中心,将△ABC放大得到△DEF,若AD=OA,△ABC的面积为4,则△DEF的面积为( )
A.2 B.8 C.16 D.24
?
8. 在平面直角坐标系中,?△ABO?的三个顶点的坐标分别为?A(-4,2)?,B(-4,0),O(0,0)?,以原点O为位似中心,把这个三角形缩小为原来的?12?,得到?△CDO?,则点A的对应点C的坐标是(? ? ? ? )
A.(-2,1) B.(2,2) C.(-2,1)或(2,-1) D.(2,2)或(-2,-2)
?
9. △A'B'C'是△ABC以点O为位似中心经过位似变换得到的,若△A'B'C'的面积与△ABC的面积比是4:9,则OB':OB为( )
A.2:3 B.3:2 C.4:5 D.4:9
?
10. 如图,将△DEF缩小为原来的一半,操作方法如下:任意取一点P,连接DP,取DP的中点A,再连接EP、FP,取它们的中点B、C,得到△ABC,则下列说法正确的有( )
①△ABC与△DEF是位似图形;②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比是1:2;④△ABC与△DEF的面积比是1:2.
A.1个 B.2个 C.3个 D.4个
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , )
?11. 如图,在 Rt△ABC ∠B=90?,AB,=3,BC=4?,点D、E分别是AC,BC的中点,点F是AD上一点,将△CEF沿EF折叠得△C'EF,C'F,交BC于点G,当△CFG,
△ABC 相似时,CF的长为________.
?
12. 如图,已知点E(-4,?2),点F(-1,?-1),以O为位似中心,把△EFO放大为原来的2倍,则E点的对应点坐标为________.
? ?
13. 如图,△ABC与△DEF是位似图形,位似比为4:9,已知AB=2,则DE的长为________.
?14. 在平面直角坐标系中,△ABC和△A'B'C'是以坐标原点O为位似中心的位似图形,且点B3,1,B'6,2.若点A2,3,则A'的坐标为________.
?
15. 已知△ABC,以点A为位似中心,作出△ADE,使△ADE是△ABC放大2倍的图形,这样的图形可以作出________个.他们之间的关系是________.
?
16. 如图,在平面直角坐标系中,△ABO三个顶点的坐标分别为A(-2,?4),B(-4,?0),O(0,?0).以原点O为位似中心,把这个三角形缩小为原来的12,得到△CDO,则点A的对应点C的坐标是________.
?
17. 如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,AB=4,则A1B1的长为________.
?
18. 在△ABC中,AB=BC,∠B=90?,将△ABC沿BC方向平移,得到△A'CC',以C为位似中心,作△DEC?与△ABC位似,位似比为1:2,F为CC'的中点,连接DF, A'F ,则A'FDF的值为________.
?
19. 如图,正方形OEFG和正方形ABCD是位似形,点F的坐标为(1,?1),点C的坐标为(4,?2),则这两个正方形位似中心的坐标是________.
三、 解答题 (本题共计 7 小题 ,共计63分 , ) ?
20. 如图,已知O是坐标原点,A,B的坐标分别为(3,1),(2,-1).
(1)在y轴的左侧以O为位似中心作△OAB的位似三角形OCD.(要求:新图与原图的相似比为 2:1);
(2)分别写出A,B的对应点C,D的坐标;
(3)若线段AB上有一点P(m,n),则点P在A'B'上的对应点P'的坐标为________.
?
21. 在如图所示的方格中,每个小正方形的边长都是1,△O1A1B1与△OAB是以点P为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)在图中标出位似中心P的位置(请保留画图痕迹);
(2)以点O为位似中心,在直线m的左侧画出△OAB的另一个位似△OA2B2,使它与△OAB的位似比为2:1,并直接写出△OA2B2与△OAB的面积之比.
?
22. 如图,已知O是坐标原点,B、C两点的坐标分别为(3,?-1)、(2,?1).
1以O点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
2分别写出B、C两点的对应点B'、C'的坐标.
?
23. 如图示,在边长为1的正方形网格中,建立如下平面直角坐标系中,其中△ABO的顶点A(3,4),B(8,1),O(0,0).
1以O为位似中心,在第一象限内作出△ABO的位似图形△A1B1O,其相似比为12.
2将△ABO绕点O逆时针旋转90?得到△A2B2O.
?
24. 如图,已知O是原点,B、C两点的坐标分别为(3,?-1),(2,?1).
(1)以点O为位似中心,在y轴的左侧将△OBC扩大为原来的两倍(即新图与原图的相似比为2),画出图形并写出点B,C的对应点的坐标;
(2)如果△OBC内部一点M的坐标为(a,?b),写出点M的对应点M'的坐标.
?
25. 在放映电影时,我们需要把胶片上的图片放大到银幕上,以便人们欣赏.如图,点P为放映机的光源,△ABC是胶片上面的画面,△A'B'C'为银幕上看到的画面.若胶片上图片的规格是2.5cm×2.5cm,放映的银幕规格是2m×2m,光源P与胶片的距离是20cm,则银幕应距离光源P多远时,放映的图象正好布满整个银幕?
?
26. 如图,已知O是坐标原点,A、B的坐标分别为(3,?1)、(2,?-1).
(1)在y轴的左侧以O为位似中心作△OAB的位似三角形OCD,使新图与原图的相似比为2:1;
(2)分别写出A,B的对应点C、D的坐标;
(3)求△OCD的面积.
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
∵ 将△OAB以点O为位似中心放大为原来的2倍,得到△OA'B',
∴ △OAB与△OA'B'的位似比为1:2,
则S△OAB:S△OA'B'=1:4.
2.
【答案】
B
【解答】
解:∵ △OAB与△OA'B'是相似比为1:2的位似图形,
△OAB内一点P(x,y)与△OA'B'内一点P'是一对对应点,
∴ P'的坐标是(-2x,-2y).
故选B.
3.
【答案】
A
【解答】
解:在平面直角坐标系中,点A6,3,以原点O为位似中心,
在第一象限内把线段OA缩小为原来的13得到线段OC,
则点A的对应点C的坐标为(6×13,3×13),
即C点坐标为2,1.
故选A.
4.
【答案】
B
【解答】
解:A、相似图形对应点的连线不一定都经过同一点,所以不一定是位似图形,错误;
B、位似图形一定是相似图形,而且位似比等于相似比,正确;
C和D选项均利用位似变换能放大图形,也能缩小图形,错误;
故选B.
5.
【答案】
B
【解答】
解:△ABO的一个顶点A的坐标是-6,2,
以原点O为位似中心相似比为1:2,将△ABO缩小得到它的位似图形△A'B'O',
∴ 点A'的坐标是:-12×6,12×2?,-12×-6,-12×2,
即-3,1或?3,-1.
故选B.
6.
【答案】
B
【解答】
解:根据图形可得,两个图形的位似比是1:2,
∴ 对应点是(-2a,?-2b).
故选B.
7.
【答案】
C
【解答】
∵ 以点O为位似中心,将△ABC放大得到△DEF,AD=OA,
∴ OA:OD=1:2,
∴ △ABC与△DEF的面积之比为:1:4,
∵ △ABC的面积为4,
∴ △DEF的面积为:16.
8.
【答案】
C
【解答】
解:∵ 点A(-4,2),且相似比为12,
∴ 当△CDO与△ABO在y轴同侧时,点C的坐标为(-2,1),
当△CDO与△ABO在y轴异侧时,点C的坐标为(2,-1).
故选C.
9.
【答案】
A
【解答】
由位似变换的性质可知,A'B',A?CIIAC,
ΔA'BC'-△ABC
ΔA'BC与△ABC的面积的比4:9
∴ ΔA'B'C’与△ABC的相似比为2:3
∴ OB'OB=23
故选A.
10.
【答案】
C
【解答】
解:由于△ABC是由△DEF缩小一半得到,所以△ABC与△DEF是位似图形,①正确;
位似图形也是相似图形,②正确;
将△DEF缩小为原来的一半,得到△ABC,所以△ABC与△DEF的位似比为1:2,所以其周长比也为1:2,③正确;
所以其面积比为1:4,④错误.
题中共有3个结论正确.
故选C.
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
11.
【答案】
4或2.8
【解答】
解:
①当FG⊥BC时,
将△CEF沿EF折叠得△C'EF,
∴ ∠C'=∠C,C'E=CE=2,
∴ sin∠C=sin∠C',
∴ ABAC=EGC'E,
∴ EG=1.2,
∵ FG//AB,
∴ CGBC=CFAC, 即
3.24=CF5,
∴ CF=4;
②当 GF⊥AC 时,如图,
将 △CEF沿EF折叠得 △C'EF,
∴ ∠1=∠2=45?,
∴ HF=HE,
∵ sin∠C=sin∠C'=EHC'E=ABAC,
∴ EH=2×35=65,
∴ C'H=C?'E2-EH2=85,
∴ CF=C'F=C'H+HF=1.6+1.2=2.8.
综上所述,当 △CFG与△ABC相似时,CF的长为4或2.8.
故答案为∶4或2.8.
12.
【答案】
(-8,?4)或(8,?-4)
【解答】
解:根据题意可知,点E对应点的坐标是E(-4,?2)的坐标同时乘以2或-2,
所以对应点的坐标为(-8,?4)或(8,?-4).
故答案为:(-8,4)或(8,-4).
13.
【答案】
92
【解答】
解:∵ △ABC与△DEF是位似图形,位似比为4:9,
∴ AB:DE=4:9,
∴ DE=92.
故答案为:92.
14.
【答案】
4,6
【解答】
解:△ABC和△A'B'C'是以坐标原点O为位似中心的位似图形,且点B3,1,B'6,2,
则△ABC和△A'B'C'的相似比为1:2,
∵ A2,3,
∴ A'的坐标为2×2,3×2,即4,6.
故答案为:4,6.
15.
【答案】
2,成中心对称
【解答】
解:以点A为位似中心,作出△ADE,使△ADE是△ABC放大2倍的图形,
可作出两个位似图形,
由于其是关于同一个点的位似图形,所以其位似图形为关于点A成中心对称.
故答案为:2,成中心对称.
16.
【答案】
(-1,?2)或(1,?-2)
【解答】
解:以原点O为位似中心,把这个三角形缩小为原来的12,点A的坐标为(-2,?4),
∴ 点C的坐标为(-2×12,?4×12)或(2×12,?-4×12),即(-1,?2)或(1,?-2).
故答案为:(-1,?2)或(1,?-2).
17.
【答案】
2
【解答】
解:∵ △ABC和△A1B1C1是以点O为位似中心的位似三角形,C1为OC的中点,AB=4,
∴ A1B1=12AB=2.
故答案为:2.
18.
【答案】
1或5
【解答】
解:设AB=BC=2x,
①如图1,当点D在AC上时,
∵ △ABC?△A'CC',
∴ A'C=CC'=2x,
∵ F为 CC'?的中点,
∴ CF=x,
则A'F=A'C2+CF2=5x,
又∵ △DEC?△ABC,且DEAB=CECB=12,
∴ DE=CE=x,
则EF=2x,
∴ DF=DE2+EF2=5x,
∴ A'FDF=5x5x=1;
②如图2,当点D在AC延长线上时,
由①知A'F=A'C2+CF2=5x,
DF=DE=x,
∴ A'FDF=5xx=5.
故答案为:1或5.
19.
【答案】
(-2,?0)
【解答】
解:两个图形位似时,位似中心就是CF与x轴的交点,
设直线CF解析式为y=kx+b,将C(4,?2),F(1,?1)代入,得
4k+b=2k+b=1,解得k=13b=23,即y=13x+23,
令y=0得x=-2,
∴ O'坐标是(-2,?0).
故答案是(-2,?0)
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
20.
【答案】
解:(1)如图:△OCD即为所求.
(2)由图可知:C:-6,-2,D:-4,2.
-2m,-2n
【解答】
解:(1)如图:△OCD即为所求.
(2)由图可知:C:-6,-2,D:-4,2.
(3)根据原点位似的特点可知P'-2m,-2n.
故答案为:-2m,-2n.
21.
【答案】
解:(1)如图所示:点P即为所求.
(2)如图所示:
△OA2B2,即为所求.
△OA2B2与△OAB的面积之比是:4:1.
【解答】
解:(1)如图所示:点P即为所求.
(2)如图所示:
△OA2B2,即为所求.
△OA2B2与△OAB的面积之比是:4:1.
22.
【答案】
解:(1)△OB'C'是所求的三角形;
2B'的坐标是(-6,?2),C'的坐标是(-4,?-2).
【解答】
解:(1)△OB'C'是所求的三角形;
2B'的坐标是(-6,?2),C'的坐标是(-4,?-2).
23.
【答案】
解:1作出位似图形如图所示,△A1B1O即为所求.
2如图△A2B2O即为所求:
【解答】
解:1作出位似图形如图所示,△A1B1O即为所求.
2如图△A2B2O即为所求:
24.
【答案】
解:(1)如图,△OB1C1为所作,点B1,C1点的坐标分别为(-6,?2),(-4,?-2);
(2)把M点的横纵坐标分别乘以-2即可得到M1的坐标,
所以点M的对应点M'的坐标为(-2a,?-2b).
【解答】
解:(1)如图,△OB1C1为所作,点B1,C1点的坐标分别为(-6,?2),(-4,?-2);
(2)把M点的横纵坐标分别乘以-2即可得到M1的坐标,
所以点M的对应点M'的坐标为(-2a,?-2b).
25.
【答案】
解:图中△A'B'C'是△ABC的位似图形,
设银幕距离光源P为xm时,放映的图象正好布满整个银幕,
则位似比=x0.2=22.5×10-2,
解得x=16.
即银幕应距离光源P为16m时,放映的图象正好布满整个银幕.
【解答】
解:图中△A'B'C'是△ABC的位似图形,
设银幕距离光源P为xm时,放映的图象正好布满整个银幕,
则位似比=x0.2=22.5×10-2,
解得x=16.
即银幕应距离光源P为16m时,放映的图象正好布满整个银幕.
26.
【答案】
如图,△OCD即为所求.
C(-6,?-2),D(-4,?2),
S△OCD=24-12×4×2-12×6×2-12×2×4=10.
【解答】
如图,△OCD即为所求.
C(-6,?-2),D(-4,?2),
S△OCD=24-12×4×2-12×6×2-12×2×4=10.
