人教版数学七年级上册 第1章 1.3有理数的加减法同步测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学七年级上册 第1章 1.3有理数的加减法同步测试试题(一)(Word版 含解析) | 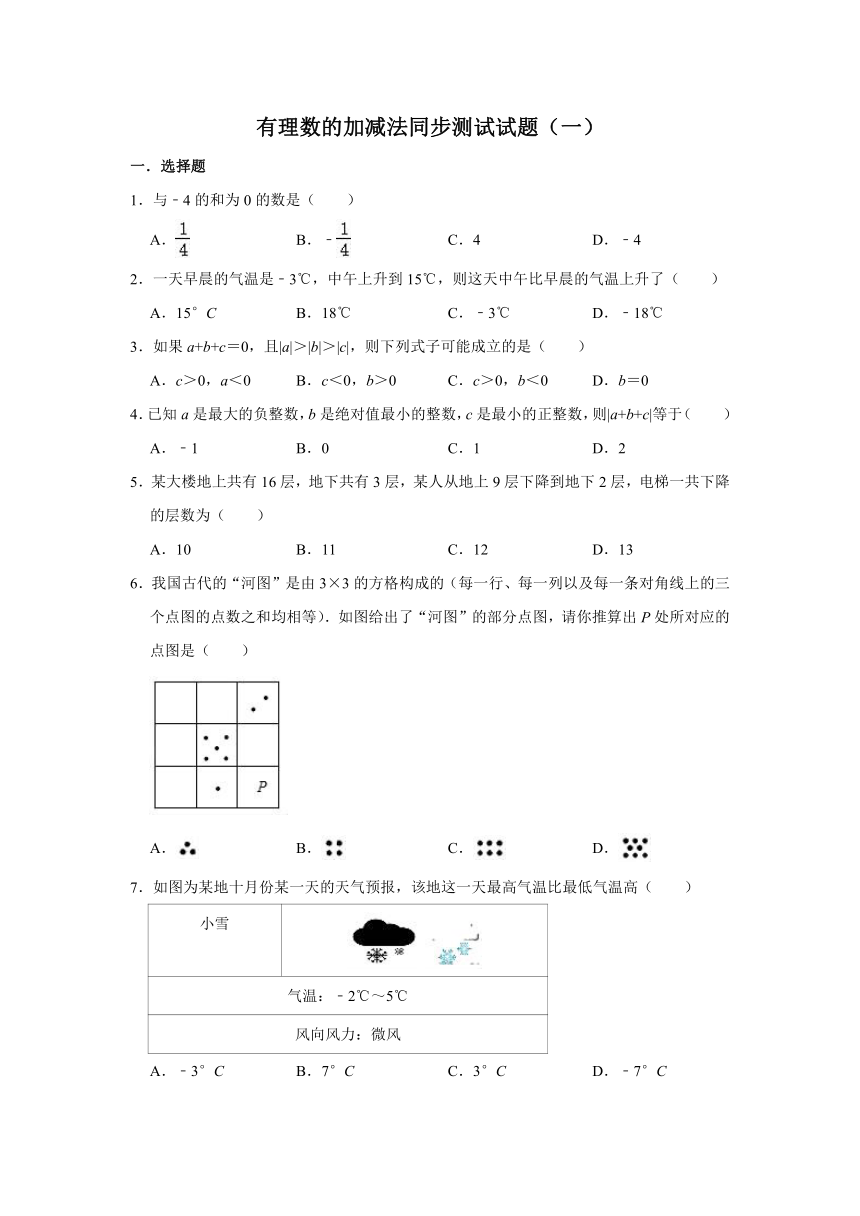 | |
| 格式 | zip | ||
| 文件大小 | 54.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 22:57:00 | ||
图片预览



文档简介
有理数的加减法同步测试试题(一)
一.选择题
1.与﹣4的和为0的数是( )
A.
B.﹣
C.4
D.﹣4
2.一天早晨的气温是﹣3℃,中午上升到15℃,则这天中午比早晨的气温上升了( )
A.15°C
B.18℃
C.﹣3℃
D.﹣18℃
3.如果a+b+c=0,且|a|>|b|>|c|,则下列式子可能成立的是( )
A.c>0,a<0
B.c<0,b>0
C.c>0,b<0
D.b=0
4.已知a是最大的负整数,b是绝对值最小的整数,c是最小的正整数,则|a+b+c|等于( )
A.﹣1
B.0
C.1
D.2
5.某大楼地上共有16层,地下共有3层,某人从地上9层下降到地下2层,电梯一共下降的层数为( )
A.10
B.11
C.12
D.13
6.我国古代的“河图”是由3×3的方格构成的(每一行、每一列以及每一条对角线上的三个点图的点数之和均相等).如图给出了“河图”的部分点图,请你推算出P处所对应的点图是( )
A.
B.
C.
D.
7.如图为某地十月份某一天的天气预报,该地这一天最高气温比最低气温高( )
小雪
气温:﹣2℃~5℃
风向风力:微风
A.﹣3°C
B.7°C
C.3°C
D.﹣7°C
8.已知a<0,b>0,|a|>|﹣b|,则a﹣b的结果是( )
A.正数
B.负数
C.0
D.无法确定
9.将式子(﹣20)+(+3)﹣(﹣5)﹣(+7)省略括号和加号后变形正确的是( )
A.20﹣3+5﹣7
B.﹣20﹣3+5+7
C.﹣20+3+5﹣7
D.﹣20﹣3+5﹣7
10.如图,在一个由6个圆圈组成的三角形里,把﹣15到﹣20这6个连续整数分别填入图的圆圈中,要求三角形的每条边上的三个数的和S都相等,那么S的最小值是( )
A.﹣53
B.﹣54
C.﹣56
D.﹣57
二.填空题
11.设a是最小的正整数,b是最大的负整数,c是绝对值最小的数,则a﹣b﹣c=
.
12.若|x|=7,|y|=5,且x+y>0,那么x﹣y=
.
13.如图,数轴上点A、B所表示的两个数的和是
.
14.A、B、C三点相对于海平面分别是﹣13米、﹣7米、﹣21米,那么最高的地方比最低的地方高
米.
15.已知|x|=2,|y|=8,且|x+y|=﹣(x+y),则3x﹣2y的值为
.
三.解答题
16.若|m|=7,n2=36,且n>m,求m+n的值.
17.已知A,B,C,D四点表示的数分别为a,b,c,d,且|c|<|b|<|a|<|d|,请化简:|a﹣c|﹣|﹣a﹣b|+|d﹣c|.
18.某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如表(规定向南为正,向北为负,单位:km):
(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
第1批
第2批
第3批
第4批
第5批
5km
2km
﹣4km
﹣3km
10km
19.|5﹣2|表示5与2两个数在数轴上所对应的两个点之间的距离.探索:
(1)求|5﹣(﹣2)|的值.
(2)如果|x+2|=1,请写出x的值.
(3)求适合条件|x﹣1|<3的所有整数x的值.
参考答案与试题解析
一.选择题
1.【解答】解:与﹣4的和为0的数,就是求出﹣4的相反数4,
故选:C.
2.【解答】解:∵一天早晨的气温是﹣3℃,中午上升到15℃,
∴这天中午比早晨的气温上升了:15﹣(﹣3)=18(℃).
故选:B.
3.【解答】解:由题目答案可知a,b,c三数中只有两正一负或两负一正两种情况,
如果假设两负一正情况合理,
要使a+b+c=0成立,
则必是b<0、c<0、a>0,
否则a+b+c≠0,
但题中并无此答案,则假设不成立.
于是应在两正一负的答案中寻找正确答案,
若a,b为正数,c为负数时,
则:|a|+|b|>|c|,
∴a+b+c≠0,
若a,c为正数,b为负数时,
则:|a|+|c|>|b|,
∴a+b+c≠0,
只有A符合题意.
故选:A.
4.【解答】解:∵a是最大的负整数,b是绝对值最小的整数,c是最小的正整数,
∴a=﹣1,b=0,c=1,
∴|a+b+c|
=|﹣1+0+1|
=0
故选:B.
5.【解答】解:根据题意得:9﹣(﹣2)﹣1=10,
则某人乘电梯从地上9层下降到地下2层,电梯一共下降的层数为10层,
故选:A.
6.【解答】解:根据行、列、对角线的和均相等,可得P+1=5+2,
解得:P=6.
故选:C.
7.【解答】解:5﹣(﹣2)=5+2=7(℃).
故选:B.
8.【解答】解:∵a<0,b>0,|a|>|﹣b|,
∴a﹣b<0,即a﹣b的结果是负数.
故选:B.
9.【解答】解:(﹣20)+(+3)﹣(﹣5)﹣(+7)=﹣20+3+5﹣7.
故选:C.
10.【解答】解:由图可知S=﹣20﹣19﹣15=﹣54.
故选:B.
二.填空题(共5小题)
11.【解答】解:∵a是最小的正整数,b是最大的负整数,c是绝对值最小的数,
∴a=1,b=﹣1,c=0,
∴a﹣b﹣c=1﹣(﹣1)﹣0=2,
故答案为:2.
12.【解答】解:∵|x|=7,|y|=5,
∴x=±7,y=±5;
∵x+y>0,
∴x=7,y=±5,
(1)x=7,y=5时,
x﹣y=7﹣5=2
(2)x=7,y=﹣5时,
x﹣y=7﹣(﹣5)=12
∴x﹣y=2或12.
故答案为:2或12.
13.【解答】解:从数轴上可知:表示点A的数为﹣3,表示点B的数是2,
则﹣3+2=﹣1.
故答案为:﹣1.
14.【解答】解:∵A、B、C三点相对于海平面分别是﹣13米、﹣7米、﹣21米,
∴最高的地方比最低的地方高:﹣7﹣(﹣21)=14(米).
故答案为:14.
15.【解答】解:∵|x|=2,|y|=8,
∴x=±2,y=±8,
∵|x+y|=﹣(x+y),
∴x+y≤0,
∴x=±2,y=﹣8,
∴3x﹣2y=3×2﹣2×(﹣8)=22,
或3x﹣2y=3×(﹣2)﹣2×(﹣8)=10.
综上所述,3x﹣2y=22或10.
故答案为:22或10.
三.解答题(共4小题)
16.【解答】解:∵|m|=7,
∴m=±7,
∵n2=36,
∴n=±6,
∵n>m,
∴①当m=﹣7时,n=﹣6,m+n=﹣7﹣6=﹣13;
②当m=﹣7时,n=6,m+n=﹣7+6=﹣1.
∴m+n=﹣13或﹣1.
17.【解答】解:∵a<b<0<c<d且|c|<|b|<|a|<|d|,
∴a﹣c<0,﹣a﹣b>0,d﹣c>0,
∴|a﹣c|﹣|﹣a﹣b|+|d﹣c|
=c﹣a+a+b+d﹣c
=b+d.
18.【解答】解:(1)5+2﹣4﹣3+10=+10(km),
因此,接送完第5批客人后,该驾驶员在公司的南方,距离公司10千米,
答:接送完第5批客人后,该驾驶员在公司的南方,距离公司10千米;
(2)0.2×(5+2+3+4+10)
=0.2×24
=4.8(升),
答:若该出租车每千米耗油0.2升,那么在这过程中共耗油4.8升;
(3)送第1批顾客收费为:10+1.8×(5﹣3)=13.6(元),
送第2批顾客收费为:10(元),
送第3批顾客收费为:10+1.8×(4﹣3)=11.8(元),
送第4批顾客收费为:10(元),
送第5批顾客收费为:10+1.8×(10﹣3)=22.6(元),
所以总收费为:13.6+10+11.8+10+22.6=68(元),
答:该驾驶员共收到车费68元.
19.【解答】解:(1)|5﹣(﹣2)|=7;
(2)∵|x+2|=1,
∴x+2=±1,
解得x=﹣3或x=﹣1
一.选择题
1.与﹣4的和为0的数是( )
A.
B.﹣
C.4
D.﹣4
2.一天早晨的气温是﹣3℃,中午上升到15℃,则这天中午比早晨的气温上升了( )
A.15°C
B.18℃
C.﹣3℃
D.﹣18℃
3.如果a+b+c=0,且|a|>|b|>|c|,则下列式子可能成立的是( )
A.c>0,a<0
B.c<0,b>0
C.c>0,b<0
D.b=0
4.已知a是最大的负整数,b是绝对值最小的整数,c是最小的正整数,则|a+b+c|等于( )
A.﹣1
B.0
C.1
D.2
5.某大楼地上共有16层,地下共有3层,某人从地上9层下降到地下2层,电梯一共下降的层数为( )
A.10
B.11
C.12
D.13
6.我国古代的“河图”是由3×3的方格构成的(每一行、每一列以及每一条对角线上的三个点图的点数之和均相等).如图给出了“河图”的部分点图,请你推算出P处所对应的点图是( )
A.
B.
C.
D.
7.如图为某地十月份某一天的天气预报,该地这一天最高气温比最低气温高( )
小雪
气温:﹣2℃~5℃
风向风力:微风
A.﹣3°C
B.7°C
C.3°C
D.﹣7°C
8.已知a<0,b>0,|a|>|﹣b|,则a﹣b的结果是( )
A.正数
B.负数
C.0
D.无法确定
9.将式子(﹣20)+(+3)﹣(﹣5)﹣(+7)省略括号和加号后变形正确的是( )
A.20﹣3+5﹣7
B.﹣20﹣3+5+7
C.﹣20+3+5﹣7
D.﹣20﹣3+5﹣7
10.如图,在一个由6个圆圈组成的三角形里,把﹣15到﹣20这6个连续整数分别填入图的圆圈中,要求三角形的每条边上的三个数的和S都相等,那么S的最小值是( )
A.﹣53
B.﹣54
C.﹣56
D.﹣57
二.填空题
11.设a是最小的正整数,b是最大的负整数,c是绝对值最小的数,则a﹣b﹣c=
.
12.若|x|=7,|y|=5,且x+y>0,那么x﹣y=
.
13.如图,数轴上点A、B所表示的两个数的和是
.
14.A、B、C三点相对于海平面分别是﹣13米、﹣7米、﹣21米,那么最高的地方比最低的地方高
米.
15.已知|x|=2,|y|=8,且|x+y|=﹣(x+y),则3x﹣2y的值为
.
三.解答题
16.若|m|=7,n2=36,且n>m,求m+n的值.
17.已知A,B,C,D四点表示的数分别为a,b,c,d,且|c|<|b|<|a|<|d|,请化简:|a﹣c|﹣|﹣a﹣b|+|d﹣c|.
18.某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如表(规定向南为正,向北为负,单位:km):
(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
第1批
第2批
第3批
第4批
第5批
5km
2km
﹣4km
﹣3km
10km
19.|5﹣2|表示5与2两个数在数轴上所对应的两个点之间的距离.探索:
(1)求|5﹣(﹣2)|的值.
(2)如果|x+2|=1,请写出x的值.
(3)求适合条件|x﹣1|<3的所有整数x的值.
参考答案与试题解析
一.选择题
1.【解答】解:与﹣4的和为0的数,就是求出﹣4的相反数4,
故选:C.
2.【解答】解:∵一天早晨的气温是﹣3℃,中午上升到15℃,
∴这天中午比早晨的气温上升了:15﹣(﹣3)=18(℃).
故选:B.
3.【解答】解:由题目答案可知a,b,c三数中只有两正一负或两负一正两种情况,
如果假设两负一正情况合理,
要使a+b+c=0成立,
则必是b<0、c<0、a>0,
否则a+b+c≠0,
但题中并无此答案,则假设不成立.
于是应在两正一负的答案中寻找正确答案,
若a,b为正数,c为负数时,
则:|a|+|b|>|c|,
∴a+b+c≠0,
若a,c为正数,b为负数时,
则:|a|+|c|>|b|,
∴a+b+c≠0,
只有A符合题意.
故选:A.
4.【解答】解:∵a是最大的负整数,b是绝对值最小的整数,c是最小的正整数,
∴a=﹣1,b=0,c=1,
∴|a+b+c|
=|﹣1+0+1|
=0
故选:B.
5.【解答】解:根据题意得:9﹣(﹣2)﹣1=10,
则某人乘电梯从地上9层下降到地下2层,电梯一共下降的层数为10层,
故选:A.
6.【解答】解:根据行、列、对角线的和均相等,可得P+1=5+2,
解得:P=6.
故选:C.
7.【解答】解:5﹣(﹣2)=5+2=7(℃).
故选:B.
8.【解答】解:∵a<0,b>0,|a|>|﹣b|,
∴a﹣b<0,即a﹣b的结果是负数.
故选:B.
9.【解答】解:(﹣20)+(+3)﹣(﹣5)﹣(+7)=﹣20+3+5﹣7.
故选:C.
10.【解答】解:由图可知S=﹣20﹣19﹣15=﹣54.
故选:B.
二.填空题(共5小题)
11.【解答】解:∵a是最小的正整数,b是最大的负整数,c是绝对值最小的数,
∴a=1,b=﹣1,c=0,
∴a﹣b﹣c=1﹣(﹣1)﹣0=2,
故答案为:2.
12.【解答】解:∵|x|=7,|y|=5,
∴x=±7,y=±5;
∵x+y>0,
∴x=7,y=±5,
(1)x=7,y=5时,
x﹣y=7﹣5=2
(2)x=7,y=﹣5时,
x﹣y=7﹣(﹣5)=12
∴x﹣y=2或12.
故答案为:2或12.
13.【解答】解:从数轴上可知:表示点A的数为﹣3,表示点B的数是2,
则﹣3+2=﹣1.
故答案为:﹣1.
14.【解答】解:∵A、B、C三点相对于海平面分别是﹣13米、﹣7米、﹣21米,
∴最高的地方比最低的地方高:﹣7﹣(﹣21)=14(米).
故答案为:14.
15.【解答】解:∵|x|=2,|y|=8,
∴x=±2,y=±8,
∵|x+y|=﹣(x+y),
∴x+y≤0,
∴x=±2,y=﹣8,
∴3x﹣2y=3×2﹣2×(﹣8)=22,
或3x﹣2y=3×(﹣2)﹣2×(﹣8)=10.
综上所述,3x﹣2y=22或10.
故答案为:22或10.
三.解答题(共4小题)
16.【解答】解:∵|m|=7,
∴m=±7,
∵n2=36,
∴n=±6,
∵n>m,
∴①当m=﹣7时,n=﹣6,m+n=﹣7﹣6=﹣13;
②当m=﹣7时,n=6,m+n=﹣7+6=﹣1.
∴m+n=﹣13或﹣1.
17.【解答】解:∵a<b<0<c<d且|c|<|b|<|a|<|d|,
∴a﹣c<0,﹣a﹣b>0,d﹣c>0,
∴|a﹣c|﹣|﹣a﹣b|+|d﹣c|
=c﹣a+a+b+d﹣c
=b+d.
18.【解答】解:(1)5+2﹣4﹣3+10=+10(km),
因此,接送完第5批客人后,该驾驶员在公司的南方,距离公司10千米,
答:接送完第5批客人后,该驾驶员在公司的南方,距离公司10千米;
(2)0.2×(5+2+3+4+10)
=0.2×24
=4.8(升),
答:若该出租车每千米耗油0.2升,那么在这过程中共耗油4.8升;
(3)送第1批顾客收费为:10+1.8×(5﹣3)=13.6(元),
送第2批顾客收费为:10(元),
送第3批顾客收费为:10+1.8×(4﹣3)=11.8(元),
送第4批顾客收费为:10(元),
送第5批顾客收费为:10+1.8×(10﹣3)=22.6(元),
所以总收费为:13.6+10+11.8+10+22.6=68(元),
答:该驾驶员共收到车费68元.
19.【解答】解:(1)|5﹣(﹣2)|=7;
(2)∵|x+2|=1,
∴x+2=±1,
解得x=﹣3或x=﹣1
