人教版七上4.3.3 余角和补角(第1课时) 课件(共27张PPT)
文档属性
| 名称 | 人教版七上4.3.3 余角和补角(第1课时) 课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
人教版
七上
第四章
几何图形初步
4.3.3
余角和补角
第1课时
余角和补角
教学重点:
余角、补角的概念及其性质.
教学难点:
余角、补角性质及规范书写几何语言.
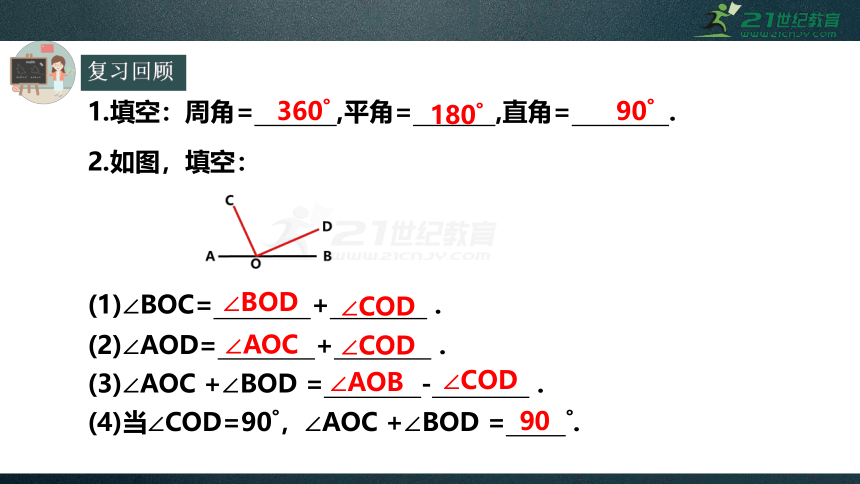
复习回顾
1.填空:周角=
,平角=
,直角=
.
2.如图,填空:
(1)∠BOC=
+
.
(2)∠AOD=
+
.
(3)∠AOC
+∠BOD
=
-
.
(4)当∠COD=90?,∠AOC
+∠BOD
=
?.
360?
180?
90?
90
∠BOD
∠COD
∠AOC
∠COD
∠AOB
∠COD
探究新知
如图,把直角三角形的直角放在直线CD上,绕着顶点O转动,两直角边与直线CD所形成∠1
和∠2,那么∠1
+∠2=
?.
90?
C
D
继续绕着顶点O转动,两直角边与直线CD所形成∠3
和∠4,那么∠3
+∠4=
?.
1
2
4
3
90?
继续绕着顶点O转动,还有这样类似的两个角吗?
归纳
如果两个角的和等于90?(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
两个角互为余角的定义:
1
2
∵∠1+∠2=90°,
∴∠1和∠2互余.
几何语言:
反之∵∠1和∠2互余,
∴∠1+∠2
=90°.
2
1
如果改变∠1的位置,它们还互余吗?
它们还互余,与角位置无关.
探究新知
类似的,如果两个角的和等于180?(平角),就说这两个角互为补角,即其中每一个角是另一个角的补角.
1
符号语言:
∵∠1+∠2=180°,
∴∠1和∠2互补.
2
如果∠1+∠2=180°,我们可以说∠1与∠2互补,或者可以说∠1是∠2的补角,还可以说∠2是∠1的补角.
反之∵∠1和∠2互补,
∴∠1+∠2
=180°.
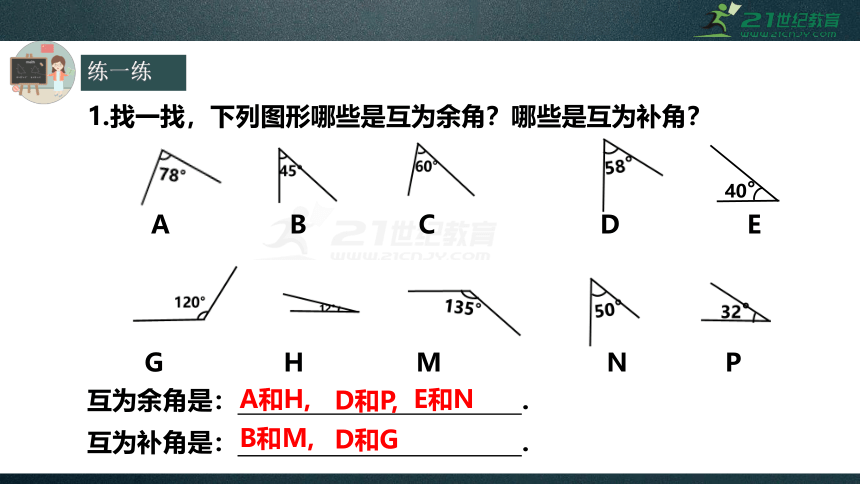
练一练
1.找一找,下列图形哪些是互为余角?哪些是互为补角?
40°
A
B
C
D
E
G
H
M
N
P
互为余角是:
.
互为补角是:
.
A和H,
D和P,
E和N
B和M,
D和G
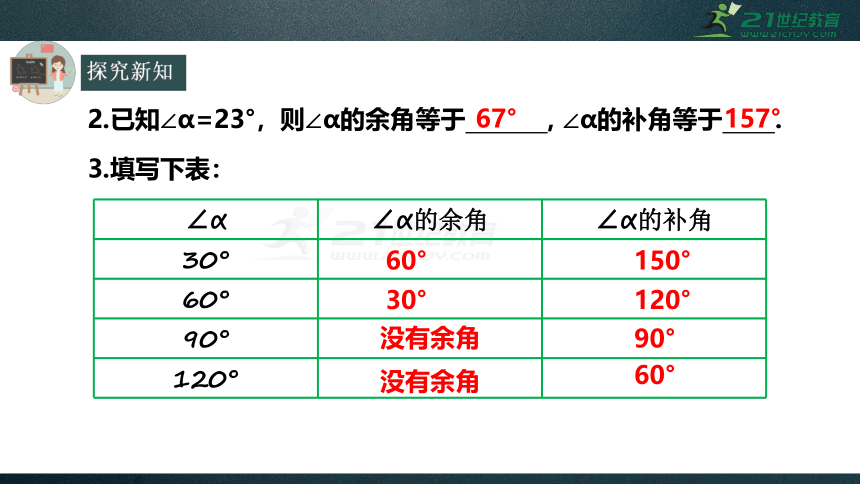
探究新知
∠α
∠α的余角
∠α的补角
30°
60°
90°
120°
2.已知∠α=23°,则∠α的余角等于
,
∠α的补角等于
.
3.填写下表:
67°
157°
60°
150°
30°
120°
没有余角
90°
60°
没有余角
归纳
1.互余、互补只是反映两个角的数量关系,与角的位置无关.互余、互补的角是成对出现的.
2.互余的两角之和等于90°,因此,锐角才有余角,直角和钝角没有余角;一个锐角的补角比它的余角大
°.
3.互补的两角之和等于180°.锐角、直角、钝角都有它的补角.
90°
例题讲解
例3.如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和
∠BOC,图中哪些角互为余角?
解:因为A,O,B在同一直线上,所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC∠BOC,所以
所以,
∠COD
和∠COE互为余角,
同理,
∠AOD
和∠BOE,∠AOD
和∠COE
,∠COD
和∠BOE也互为余角.
∠COD
+∠COE=
∠AOC
+
∠BOC
=
(∠AOC
+∠BOC)
=90°
练一练
如图,O是直线AB上一点,OE是∠AOB的平分线,则
(1)∠AOD的余角是
,
∠AOD的补角是
,
(2)∠BOC的余角是
,
∠BOC的补角是
,
(3)∠BOD的补角是
,
∠BOD的补角的余角是
.
∠DOE
∠BOD
∠COE
∠AOC
∠AOD
∠DOE
探究新知
如图,O是直线AB上的一点,OC
平分∠AOB
,
∠EOF=90°
,则图中有哪些角相等?并说明理由.
解:
∠1=
∠3
,∠2
=∠4.
理由:
∵O是直线AB上的一点,OC
平分∠AOB.
∴∠AOC=
∠BOC=90°
∵
∠1+
∠2
=90°,
∠2
+∠3
=90°.
∴∠1=
∠3.
同理可得:∠2
=∠4.
余角的性质:
归纳
同角(等角)的余角相等.
几何语言:
∵
∠1+
∠2
=90°,
∠2
+∠3
=90°.
∴∠1=
∠3.
或∵
∠1=∠3,
∠1+
∠2
=90°,
∠3
+∠4
=90°.
∴∠2=
∠4.
探究新知
思考:已知∠1与∠2,∠3都互为补角.那么∠2和∠3的大小有什么关系?
所以∠2=∠3.
解:由∠1与∠2和∠3都互为补角,
那么
∠1+∠2
=180?
,
∠1+∠3
=180?
,
归纳
同角(等角)的补角相等.
几何语言:
∵
∠1+
∠2
=180°,
∠2
+∠3
=180°.
∴∠1=
∠3.
或∵
∠1=∠3,
∠1+
∠2
=180°,
∠3
+∠4
=180°.
∴∠2=
∠4.
练一练
1.
若∠1+∠2=90°,∠1+∠3=90°,那么∠2与∠3的关系为:∠1
∠2
(“>”,”<”,”=”).
2.
若∠1是∠3的余角,∠2是∠4的余角,且∠3=∠4,那么∠1与∠2的关系为:∠1
∠2
(“>”,”<”,”=”).
3.若∠1与∠2互补,∠1与∠3互余,则∠2与∠3的差为
.
=
=
90°
探究新知
(补充例题)
若一个角的补角比它的余角的3倍少10°,求这个角的度数.
解:设这个角是x度,则它的余角是(90°-x)它的补角是(180°-x),
根据题意得:
180°-x=3(90°-x)-
10°
解得x=40°
答:这个角的度数是40°.
练一练
若一个角的补角等于它的余角的4倍,求这个角的度数.
解:设这个角是x度,则它的补角是(180-x),余角是(90-x),根据题意得:
180°-x=4(90°-x)
x=60°
这个角的度数是60°.
课堂练习
1.若∠α与∠β互补,∠β与∠γ互补,则∠α与∠γ的关系是(
).
A
互余
B
互补
C
相等
D
不能确定
2.下列说法正确的是( ).
A
一个角的补角一定大于它本身
B
一个角的余角一定小于它本身
C
一个钝角减去一个锐角的差一定是一个锐角
D
一个角的余角一定小于其补角
C
D
课堂练习
3.因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2的依据是( ).
A
同角的余角相等
B
等角的余角相等
C
同角的补角相等
D
等角的补角相等
4.因为∠1+∠2=90°,∠3+∠4=90°,
∠1=∠2,所以∠3=∠4的依据是( ).
A
同角的余角相等
B
等角的余角相等
C
同角的补角相等
D
等角的补角相等
C
B
课堂练习
5.
如果一个角的余角等于它本身,那么这个角等于_______;若一个角的补角等于它本身,则这个角等于_______.
6.
若∠α与∠β互余,
∠α=20°,则∠β=
,∠α的补角是
.
7.
若∠1与∠2互补,∠3与∠4互补,则∠2=∠4,
∠1=70°,则∠3=
.
45°
90°
70°
160°
70°
8.一个角的余角比它的补角的
少20°,则这个角为
.
70°
课堂练习
9.已知O是直线AB上的一点,
∠3=56°,∠MON=90°,OM是∠AOC的平分线.
(1)求∠1的度数.
(2)找出图中与∠2互余的角,并说明理由..
(3)图中有∠3的补角吗?若有,请把它找出来,并说明理由.
课堂练习
(1)解:∵∠3=56°,∠MON=90°,
∠2+∠3=MON
∴∠2=34°.
∵OM是∠AOC的平分线.
∴∠1=∠2=34°.
∵
∠2+∠3=MON
,∠MON=90°.
∴∠2+∠3=90°.
(2)解:由(1)
得知∠1=∠2,∠MON=90°,
∠1+∠MON+∠4=180°.
∴
∠1+∠4=90°,
∠2+∠4=90°.
与∠2余角的有∠3,
∠4.
课堂练习
(3)解:有,∠3的补角是∠AON.
由(2)
得知∠2的余角有∠3,∠4,
即:∠2+∠3=90°,
∠2+∠4=90°.
∴∠3=∠4(同角的余角相等).
∵∠AON+∠4=180°
∴∠AON+∠3=180°(等量代换).
∴∠3的补角是∠AON.
课堂小结
1.互为余角、补角的定义:
2.
余角、补角的性质:
课外作业
习题4.3
第140页第11题
第140页第13题
https://www.21cnjy.com/help/help_extract.php
人教版
七上
第四章
几何图形初步
4.3.3
余角和补角
第1课时
余角和补角
教学重点:
余角、补角的概念及其性质.
教学难点:
余角、补角性质及规范书写几何语言.
复习回顾
1.填空:周角=
,平角=
,直角=
.
2.如图,填空:
(1)∠BOC=
+
.
(2)∠AOD=
+
.
(3)∠AOC
+∠BOD
=
-
.
(4)当∠COD=90?,∠AOC
+∠BOD
=
?.
360?
180?
90?
90
∠BOD
∠COD
∠AOC
∠COD
∠AOB
∠COD
探究新知
如图,把直角三角形的直角放在直线CD上,绕着顶点O转动,两直角边与直线CD所形成∠1
和∠2,那么∠1
+∠2=
?.
90?
C
D
继续绕着顶点O转动,两直角边与直线CD所形成∠3
和∠4,那么∠3
+∠4=
?.
1
2
4
3
90?
继续绕着顶点O转动,还有这样类似的两个角吗?
归纳
如果两个角的和等于90?(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
两个角互为余角的定义:
1
2
∵∠1+∠2=90°,
∴∠1和∠2互余.
几何语言:
反之∵∠1和∠2互余,
∴∠1+∠2
=90°.
2
1
如果改变∠1的位置,它们还互余吗?
它们还互余,与角位置无关.
探究新知
类似的,如果两个角的和等于180?(平角),就说这两个角互为补角,即其中每一个角是另一个角的补角.
1
符号语言:
∵∠1+∠2=180°,
∴∠1和∠2互补.
2
如果∠1+∠2=180°,我们可以说∠1与∠2互补,或者可以说∠1是∠2的补角,还可以说∠2是∠1的补角.
反之∵∠1和∠2互补,
∴∠1+∠2
=180°.
练一练
1.找一找,下列图形哪些是互为余角?哪些是互为补角?
40°
A
B
C
D
E
G
H
M
N
P
互为余角是:
.
互为补角是:
.
A和H,
D和P,
E和N
B和M,
D和G
探究新知
∠α
∠α的余角
∠α的补角
30°
60°
90°
120°
2.已知∠α=23°,则∠α的余角等于
,
∠α的补角等于
.
3.填写下表:
67°
157°
60°
150°
30°
120°
没有余角
90°
60°
没有余角
归纳
1.互余、互补只是反映两个角的数量关系,与角的位置无关.互余、互补的角是成对出现的.
2.互余的两角之和等于90°,因此,锐角才有余角,直角和钝角没有余角;一个锐角的补角比它的余角大
°.
3.互补的两角之和等于180°.锐角、直角、钝角都有它的补角.
90°
例题讲解
例3.如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和
∠BOC,图中哪些角互为余角?
解:因为A,O,B在同一直线上,所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC∠BOC,所以
所以,
∠COD
和∠COE互为余角,
同理,
∠AOD
和∠BOE,∠AOD
和∠COE
,∠COD
和∠BOE也互为余角.
∠COD
+∠COE=
∠AOC
+
∠BOC
=
(∠AOC
+∠BOC)
=90°
练一练
如图,O是直线AB上一点,OE是∠AOB的平分线,则
(1)∠AOD的余角是
,
∠AOD的补角是
,
(2)∠BOC的余角是
,
∠BOC的补角是
,
(3)∠BOD的补角是
,
∠BOD的补角的余角是
.
∠DOE
∠BOD
∠COE
∠AOC
∠AOD
∠DOE
探究新知
如图,O是直线AB上的一点,OC
平分∠AOB
,
∠EOF=90°
,则图中有哪些角相等?并说明理由.
解:
∠1=
∠3
,∠2
=∠4.
理由:
∵O是直线AB上的一点,OC
平分∠AOB.
∴∠AOC=
∠BOC=90°
∵
∠1+
∠2
=90°,
∠2
+∠3
=90°.
∴∠1=
∠3.
同理可得:∠2
=∠4.
余角的性质:
归纳
同角(等角)的余角相等.
几何语言:
∵
∠1+
∠2
=90°,
∠2
+∠3
=90°.
∴∠1=
∠3.
或∵
∠1=∠3,
∠1+
∠2
=90°,
∠3
+∠4
=90°.
∴∠2=
∠4.
探究新知
思考:已知∠1与∠2,∠3都互为补角.那么∠2和∠3的大小有什么关系?
所以∠2=∠3.
解:由∠1与∠2和∠3都互为补角,
那么
∠1+∠2
=180?
,
∠1+∠3
=180?
,
归纳
同角(等角)的补角相等.
几何语言:
∵
∠1+
∠2
=180°,
∠2
+∠3
=180°.
∴∠1=
∠3.
或∵
∠1=∠3,
∠1+
∠2
=180°,
∠3
+∠4
=180°.
∴∠2=
∠4.
练一练
1.
若∠1+∠2=90°,∠1+∠3=90°,那么∠2与∠3的关系为:∠1
∠2
(“>”,”<”,”=”).
2.
若∠1是∠3的余角,∠2是∠4的余角,且∠3=∠4,那么∠1与∠2的关系为:∠1
∠2
(“>”,”<”,”=”).
3.若∠1与∠2互补,∠1与∠3互余,则∠2与∠3的差为
.
=
=
90°
探究新知
(补充例题)
若一个角的补角比它的余角的3倍少10°,求这个角的度数.
解:设这个角是x度,则它的余角是(90°-x)它的补角是(180°-x),
根据题意得:
180°-x=3(90°-x)-
10°
解得x=40°
答:这个角的度数是40°.
练一练
若一个角的补角等于它的余角的4倍,求这个角的度数.
解:设这个角是x度,则它的补角是(180-x),余角是(90-x),根据题意得:
180°-x=4(90°-x)
x=60°
这个角的度数是60°.
课堂练习
1.若∠α与∠β互补,∠β与∠γ互补,则∠α与∠γ的关系是(
).
A
互余
B
互补
C
相等
D
不能确定
2.下列说法正确的是( ).
A
一个角的补角一定大于它本身
B
一个角的余角一定小于它本身
C
一个钝角减去一个锐角的差一定是一个锐角
D
一个角的余角一定小于其补角
C
D
课堂练习
3.因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2的依据是( ).
A
同角的余角相等
B
等角的余角相等
C
同角的补角相等
D
等角的补角相等
4.因为∠1+∠2=90°,∠3+∠4=90°,
∠1=∠2,所以∠3=∠4的依据是( ).
A
同角的余角相等
B
等角的余角相等
C
同角的补角相等
D
等角的补角相等
C
B
课堂练习
5.
如果一个角的余角等于它本身,那么这个角等于_______;若一个角的补角等于它本身,则这个角等于_______.
6.
若∠α与∠β互余,
∠α=20°,则∠β=
,∠α的补角是
.
7.
若∠1与∠2互补,∠3与∠4互补,则∠2=∠4,
∠1=70°,则∠3=
.
45°
90°
70°
160°
70°
8.一个角的余角比它的补角的
少20°,则这个角为
.
70°
课堂练习
9.已知O是直线AB上的一点,
∠3=56°,∠MON=90°,OM是∠AOC的平分线.
(1)求∠1的度数.
(2)找出图中与∠2互余的角,并说明理由..
(3)图中有∠3的补角吗?若有,请把它找出来,并说明理由.
课堂练习
(1)解:∵∠3=56°,∠MON=90°,
∠2+∠3=MON
∴∠2=34°.
∵OM是∠AOC的平分线.
∴∠1=∠2=34°.
∵
∠2+∠3=MON
,∠MON=90°.
∴∠2+∠3=90°.
(2)解:由(1)
得知∠1=∠2,∠MON=90°,
∠1+∠MON+∠4=180°.
∴
∠1+∠4=90°,
∠2+∠4=90°.
与∠2余角的有∠3,
∠4.
课堂练习
(3)解:有,∠3的补角是∠AON.
由(2)
得知∠2的余角有∠3,∠4,
即:∠2+∠3=90°,
∠2+∠4=90°.
∴∠3=∠4(同角的余角相等).
∵∠AON+∠4=180°
∴∠AON+∠3=180°(等量代换).
∴∠3的补角是∠AON.
课堂小结
1.互为余角、补角的定义:
2.
余角、补角的性质:
课外作业
习题4.3
第140页第11题
第140页第13题
https://www.21cnjy.com/help/help_extract.php
