苏科版九年级下册数学 下册 7.5解直角三角形练习(Word版 含答案)
文档属性
| 名称 | 苏科版九年级下册数学 下册 7.5解直角三角形练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 96.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 23:16:43 | ||
图片预览


文档简介
锐角三角函数章节------解直角三角形(含答案)
知识梳理:
1
三边之间的关系:
a?+b?=c?
2
两锐角之间的关系:
∠A+∠B=90
3.
边与角之间的关系:sinA=
cosA=
tanA=
总结:由直角三角形中的已知元素求出其他未知元素的过程,叫做解直角三角形。
例题讲解:
例1.
如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D′处,那么tan∠BAD′等于(
)
(A).1
(B).
(C).
(D).
例2、如果a是锐角,且cosa=,那么sina的值是(
).
(A)
(B)
(C)
(D)
例3、等腰三角形底边长为10㎝,周长为36cm,那么底角的余弦等于(
).
(A)
(B)
(C)
(D)
例4、在Rt△ABC中,∠C=90°,下列式子中正确的是(
).
(A)sinA=sinB
(B)sinA=cosB
(C)tanA=tanB
(D)cotA=cotB
例5、已知α为锐角,tan(90°-α)=,则α的度数为(
)
(A)30°
(B)45°
(C)60°
(D)75°
例6、如果∠a是等边三角形的一个内角,那么cosa的值等于(
).
(A)
(B)
(C)
(D)1
例7、如图,在△ABC中,若∠A=30°,∠B=45°,AC=,则BC=
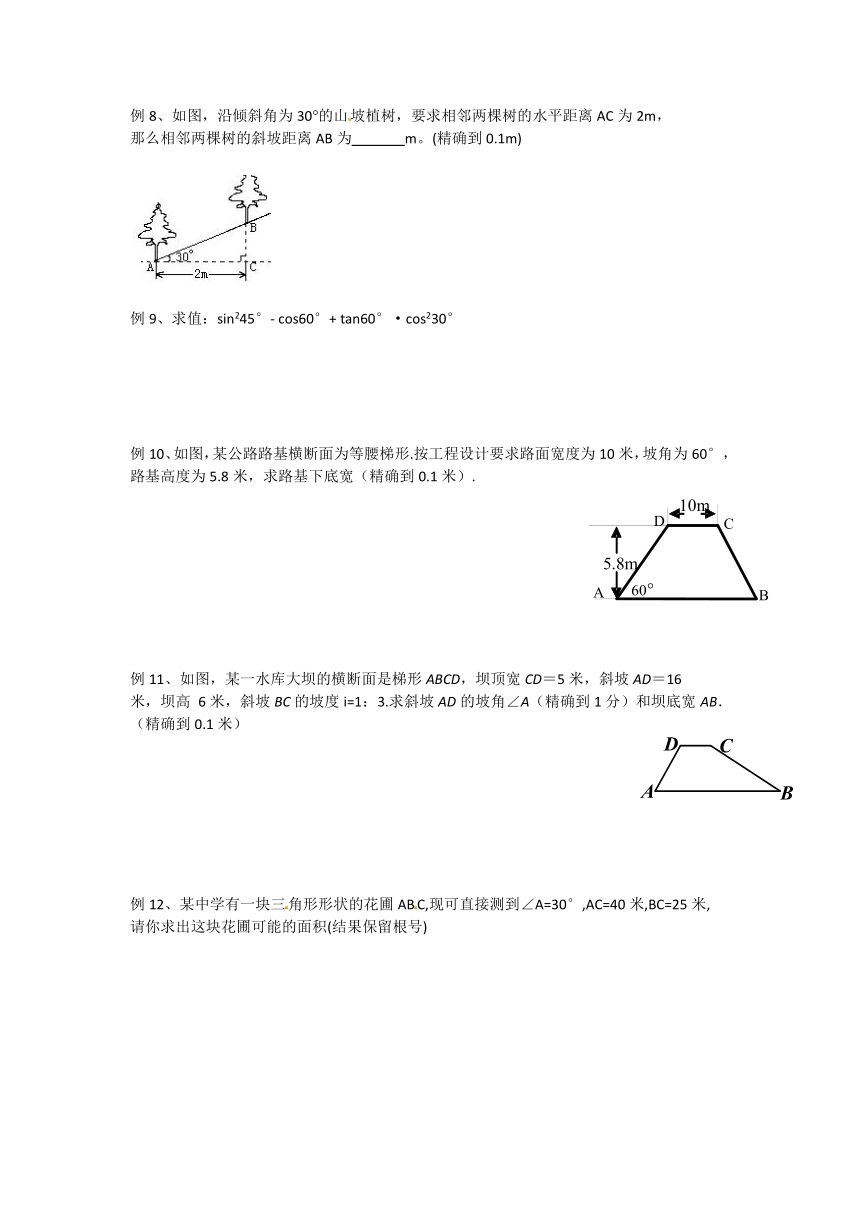
例8、如图,沿倾斜角为30的山坡植树,要求相邻两棵树的水平距离AC为2m,
那么相邻两棵树的斜坡距离AB为
m。(精确到0.1m)
例9、求值:sin245°-
cos60°+
tan60°·cos230°
例10、如图,某公路路基横断面为等腰梯形.按工程设计要求路面宽度为10米,坡角为60°,
路基高度为5.8米,求路基下底宽(精确到0.1米).
例11、如图,某一水库大坝的横断面是梯形ABCD,坝顶宽CD=5米,斜坡AD=16
米,坝高
6米,斜坡BC的坡度i=1:3.求斜坡AD的坡角∠A(精确到1分)和坝底宽AB.
(精确到0.1米)
例12、某中学有一块三角形形状的花圃ABC,现可直接测到∠A=30°,AC=40米,BC=25米,
请你求出这块花圃可能的面积(结果保留根号)
巩固练习:
1.如图,在Rt△ABC中,除∠C=90°外,其余______个元素之间存在以下关系:
(l)三边之间的关系:____________(也就是__________定理);
(2)两个锐角之间的关系:____________;
(3)边角之间的关系:sin
A=________,cos
A=________,tan
A=_________.
2.如图,在梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,AD=4,AB=3,则底BC的长为_______.
3.在△ABC中,∠C=90°,a=3,c=2,则∠B=________.
4.在△ABC中,∠C=90°,∠A=45°,c=6,则b=________.
5.在Rt△ABC中,∠C=90°,BC=,AC=,则∠A的度数为
(
)
A.90°
B.60°
C.45°
D.30°
6.在Rt△ABC中,∠C=90°,则在下列边角之间的关系中,正确的是
(
)
A.b=csin
A
B.a=btan
A
C.a=btan
B
D.b=ccos
B
7.在△ABC中,∠C=90°,tan
A=,则sin
B的值为
(
)
A.
B.
C.
D.
8.如图,在△ABC中,cosB=,sinC=,AC=5,则△ABC的面积是(
)
A.
B.12
C.14
D.21
9.如图,为了测量河两岸A、B两点的距离,在与AB垂直的方向
点C处测得AC=a,∠ACB=α,则AB的长为
(
)
A.a
.sin
α
B.a
.tan
α
C.a
.cos
α
D.
10.
在Rt△ABC中,∠C=90°.根据下列条件解直角三角形:
(1)已知c=20,∠A=45°;
(2)已知a=36,∠B=30°;
(3)已知a=19,c=19;
(4)a=6,b=6.
11.如图,在菱形ABCD中,AE⊥BC于E点,EC=1,sinB=.求四边形ABCD的周长.
12.
如图,在△ABC中,∠C=90°,D是BC的中点,∠ADC=60°,AC=,求△ABD的周长.
13.如图,某居民楼I高20米,窗户朝南,该楼内一楼住户的窗台到地面的距离CM为2米,窗户CD高1.8米.现计划在I楼的正南方向距I楼30米处新建一居民楼Ⅱ.当正午时刻太阳光线与地面成30°角时,要使Ⅱ楼的影子不影响I楼所有住户的采光,新建Ⅱ楼最高只能盖多少米?
14.在Rt△ABC中,∠C=90°,b+c=24,∠A-∠B=30°,解此直角三角形.
15.如图,在△ABC中∠C=90°,∠A=45°,D为AC上一点,∠BDC=60°,AD=2,求BC的长.
16.已知等腰三角形的底边长为20
cm,面积为cm2,求此三角形各内角的度数.
17.如图,⊙O的直径AB与弦CD相交于点E,弧BC=弧BD,⊙O的切线BF与弦AD的延长线相交于点F,连接BC,若⊙O的半径为4,cos∠BCD=,求线段AD、CD的长.
18.
如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取=1.732,结果精确到1m)
巩固练习答案:
1.5
(1)
a2+b2
=c2
勾股
(2)
∠A+∠B=90°
(3)
2.10
3.30°
4.3
5.D
6.B
7.D
8.A
9.B
10.(1)∠B=45°,a=10,b=10
(2)∠A=60°,b=12,c=24
(3)∠A=45°,∠B=45°,b=19
(4)∠A=30°,∠B=60°,c=12
11.可以求得边长为13,则四边形ABCD的周长为52.
12.△ABD的周长为
13.新建居民楼Ⅱ最高只能盖(10+2)米
14.
∠A=60°,∠B=30°,a=8,b=8,c=16
15.BC的长为+1
16.三个内角分别为30°、30°、120°
17.AD=6,
CD=3
18.
设CE=xm,则由题意可知BE=xm,AE=(x+100)m.
在Rt△AEC中,tan∠CAE=,即tan30°=
∴,3x=(x+100)
解得x=50+50=136.6
∴CD=CE+ED=(136.6+1.5)=138.1≈138(m)
知识梳理:
1
三边之间的关系:
a?+b?=c?
2
两锐角之间的关系:
∠A+∠B=90
3.
边与角之间的关系:sinA=
cosA=
tanA=
总结:由直角三角形中的已知元素求出其他未知元素的过程,叫做解直角三角形。
例题讲解:
例1.
如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D′处,那么tan∠BAD′等于(
)
(A).1
(B).
(C).
(D).
例2、如果a是锐角,且cosa=,那么sina的值是(
).
(A)
(B)
(C)
(D)
例3、等腰三角形底边长为10㎝,周长为36cm,那么底角的余弦等于(
).
(A)
(B)
(C)
(D)
例4、在Rt△ABC中,∠C=90°,下列式子中正确的是(
).
(A)sinA=sinB
(B)sinA=cosB
(C)tanA=tanB
(D)cotA=cotB
例5、已知α为锐角,tan(90°-α)=,则α的度数为(
)
(A)30°
(B)45°
(C)60°
(D)75°
例6、如果∠a是等边三角形的一个内角,那么cosa的值等于(
).
(A)
(B)
(C)
(D)1
例7、如图,在△ABC中,若∠A=30°,∠B=45°,AC=,则BC=
例8、如图,沿倾斜角为30的山坡植树,要求相邻两棵树的水平距离AC为2m,
那么相邻两棵树的斜坡距离AB为
m。(精确到0.1m)
例9、求值:sin245°-
cos60°+
tan60°·cos230°
例10、如图,某公路路基横断面为等腰梯形.按工程设计要求路面宽度为10米,坡角为60°,
路基高度为5.8米,求路基下底宽(精确到0.1米).
例11、如图,某一水库大坝的横断面是梯形ABCD,坝顶宽CD=5米,斜坡AD=16
米,坝高
6米,斜坡BC的坡度i=1:3.求斜坡AD的坡角∠A(精确到1分)和坝底宽AB.
(精确到0.1米)
例12、某中学有一块三角形形状的花圃ABC,现可直接测到∠A=30°,AC=40米,BC=25米,
请你求出这块花圃可能的面积(结果保留根号)
巩固练习:
1.如图,在Rt△ABC中,除∠C=90°外,其余______个元素之间存在以下关系:
(l)三边之间的关系:____________(也就是__________定理);
(2)两个锐角之间的关系:____________;
(3)边角之间的关系:sin
A=________,cos
A=________,tan
A=_________.
2.如图,在梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,AD=4,AB=3,则底BC的长为_______.
3.在△ABC中,∠C=90°,a=3,c=2,则∠B=________.
4.在△ABC中,∠C=90°,∠A=45°,c=6,则b=________.
5.在Rt△ABC中,∠C=90°,BC=,AC=,则∠A的度数为
(
)
A.90°
B.60°
C.45°
D.30°
6.在Rt△ABC中,∠C=90°,则在下列边角之间的关系中,正确的是
(
)
A.b=csin
A
B.a=btan
A
C.a=btan
B
D.b=ccos
B
7.在△ABC中,∠C=90°,tan
A=,则sin
B的值为
(
)
A.
B.
C.
D.
8.如图,在△ABC中,cosB=,sinC=,AC=5,则△ABC的面积是(
)
A.
B.12
C.14
D.21
9.如图,为了测量河两岸A、B两点的距离,在与AB垂直的方向
点C处测得AC=a,∠ACB=α,则AB的长为
(
)
A.a
.sin
α
B.a
.tan
α
C.a
.cos
α
D.
10.
在Rt△ABC中,∠C=90°.根据下列条件解直角三角形:
(1)已知c=20,∠A=45°;
(2)已知a=36,∠B=30°;
(3)已知a=19,c=19;
(4)a=6,b=6.
11.如图,在菱形ABCD中,AE⊥BC于E点,EC=1,sinB=.求四边形ABCD的周长.
12.
如图,在△ABC中,∠C=90°,D是BC的中点,∠ADC=60°,AC=,求△ABD的周长.
13.如图,某居民楼I高20米,窗户朝南,该楼内一楼住户的窗台到地面的距离CM为2米,窗户CD高1.8米.现计划在I楼的正南方向距I楼30米处新建一居民楼Ⅱ.当正午时刻太阳光线与地面成30°角时,要使Ⅱ楼的影子不影响I楼所有住户的采光,新建Ⅱ楼最高只能盖多少米?
14.在Rt△ABC中,∠C=90°,b+c=24,∠A-∠B=30°,解此直角三角形.
15.如图,在△ABC中∠C=90°,∠A=45°,D为AC上一点,∠BDC=60°,AD=2,求BC的长.
16.已知等腰三角形的底边长为20
cm,面积为cm2,求此三角形各内角的度数.
17.如图,⊙O的直径AB与弦CD相交于点E,弧BC=弧BD,⊙O的切线BF与弦AD的延长线相交于点F,连接BC,若⊙O的半径为4,cos∠BCD=,求线段AD、CD的长.
18.
如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取=1.732,结果精确到1m)
巩固练习答案:
1.5
(1)
a2+b2
=c2
勾股
(2)
∠A+∠B=90°
(3)
2.10
3.30°
4.3
5.D
6.B
7.D
8.A
9.B
10.(1)∠B=45°,a=10,b=10
(2)∠A=60°,b=12,c=24
(3)∠A=45°,∠B=45°,b=19
(4)∠A=30°,∠B=60°,c=12
11.可以求得边长为13,则四边形ABCD的周长为52.
12.△ABD的周长为
13.新建居民楼Ⅱ最高只能盖(10+2)米
14.
∠A=60°,∠B=30°,a=8,b=8,c=16
15.BC的长为+1
16.三个内角分别为30°、30°、120°
17.AD=6,
CD=3
18.
设CE=xm,则由题意可知BE=xm,AE=(x+100)m.
在Rt△AEC中,tan∠CAE=,即tan30°=
∴,3x=(x+100)
解得x=50+50=136.6
∴CD=CE+ED=(136.6+1.5)=138.1≈138(m)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
