苏科版九年级下册数学 下册 7.6锐角三角函数的简单应用练习(Word版 含答案)
文档属性
| 名称 | 苏科版九年级下册数学 下册 7.6锐角三角函数的简单应用练习(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 197.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览




文档简介
锐角三角函数章节------锐角三角函数的简单应用练习(含答案)
知识梳理:
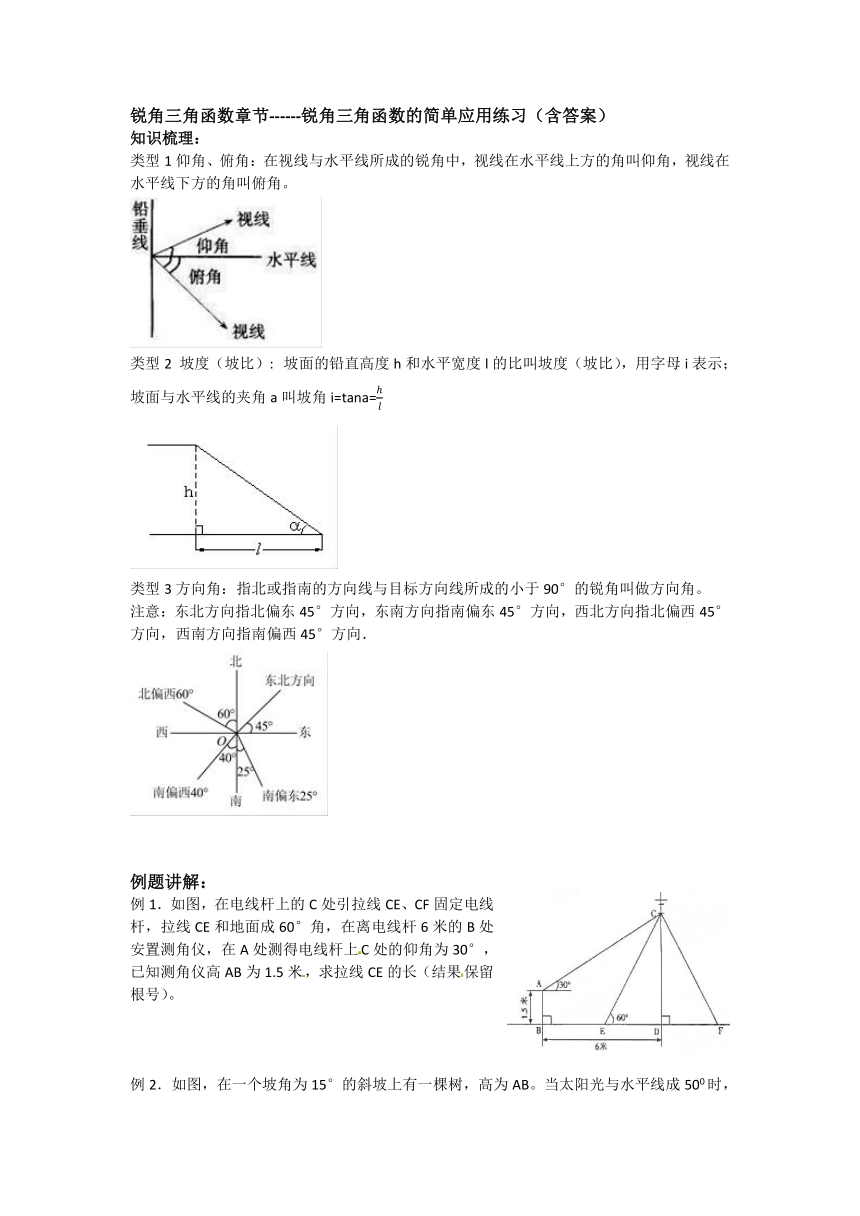
类型1仰角、俯角:在视线与水平线所成的锐角中,视线在水平线上方的角叫仰角,视线在水平线下方的角叫俯角。
类型2
坡度(坡比):
坡面的铅直高度h和水平宽度l的比叫坡度(坡比),用字母i表示;坡面与水平线的夹角a叫坡角i=tana=
类型3方向角:指北或指南的方向线与目标方向线所成的小于90°的锐角叫做方向角。
注意:东北方向指北偏东45°方向,东南方向指南偏东45°方向,西北方向指北偏西45°方向,西南方向指南偏西45°方向.
例题讲解:
例1.如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号)。
例2.如图,在一个坡角为15°的斜坡上有一棵树,高为AB。当太阳光与水平线成500时,测得该树在斜坡上的树影BC的长为7m,求树高。(精确到0.1m)
例3.要在宽为28m的海堤公路的路边安装路灯。路灯的灯臂长为3m,且与灯柱成120°(如图所示),路灯采用圆锥形灯罩,灯罩的轴线与灯臂垂直。当灯罩的轴线通过公路路面的中线时,照明效果最理想。问:应设计多高的灯柱,才能取得最理想的照明效果?
例4.已知:如图,在△ABC中,∠CAB=120°,AB=4,AC=2,AD⊥BC,D是垂足。求:AD的长。
例5.如图,甲、乙两只捕捞船同时从A港出海捕鱼。甲船以每小时15千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进。甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇。
(1)甲船从C处追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是每小时多少千米?
例6.如图,在A、B两座工厂之间要修建一条笔直的公路,从A地测得B地的走向是南偏东52°,现A、B两地要同时开工,若干天后公路准确对接,则B地所修公路的走向应该是(
)
A北偏西52°
B南偏东52°
C西偏北52°
D北偏西
例7.梯形护坡石坝的斜坡AB的坡度i=1:3,坝高BC为2米,则斜坡AB的长是多少米?坡角为多少度?
例8.如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.问:8秒后船向岸边移动了多少米?(结果精确到0.1米)
例9.据气象台预报,一强台风的中心位于宁波(指城区,下同)东南方向(36)千米的海面上,目前台风中心正以20千米/时的速度向北偏西60°的方向移动,距台风中心50千米的圆形区域均会受到强袭击.已知宁海位于宁波正南方向72千米处,象山位于宁海北偏东60°方向56千米处.请问:宁波、宁海、象山是否会受这次台风的强袭击?如果会,请求出受强袭击的时间;如果不会,请说明理由.
(为解决问题,须画出示意图,现已画出其中一部分,请根据需要,把图形画完整)
巩固练习:
1.如图,先锋村准备在坡角为α的山坡上栽树,如果要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为
(
)
A.5cosa米
B.米
C.5sina米
D.米
2.如图,AB是伸缩式的遮阳棚,CD是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,则AB的长度是______米(假设夏至的正午时刻阳光与地平面的夹角为60°).
3.如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处正东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=________米(用根号表示).
4.某校兴趣小组乘坐游轮拍摄海河两岸美景.如图,游轮出发点A与望海楼B的距离为300
m.在A处测得望海楼B位于A的北偏东30°方向,游轮沿正北方向行驶一段时间后到达C,在C处测得望海楼B位于C的北偏东60°方向,求此时游轮与望海楼之间的距离BC的长(≈1.73,结果保留整数).
5.兵兵家的一棵树因台风于A处折断,如图所示,测得树梢触地点B
到树根C处的距离为4米,∠ABC约为45°,树干AC垂直于地面,
那么此树在未折断之前的高度约为________米(答案可保留根号).
6.已知等腰梯形的腰长是4cm,下底长为8
cm,底角的余弦值为,则这个梯形的上底长为(
)
A.8
cm
B.6
cm
C.4
cm
D.2
cm
7.如图,甲、乙为两个高度相等且底面直径之比为1:2的圆柱形水杯,甲杯装满液体,乙杯是空杯.若把甲杯中的液体全部倒入乙杯,则乙杯中的液面与图中点P的距离是________cm.
8.如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5
m(即小颖的眼睛与地面的距离),那么这棵树高
(
)
A.(+)m
B.(5+)m
C.
m
D.4m
9.如图,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,如果这时气球的高度CD为150米,且点A、D、B在同一直线上,那么建筑物A、B间的距离为(
)
A.150米
B.180米
C.200米
D.220米
10.某广电大楼顶部有一发射塔,在地面B处测得楼顶D的仰角为30°,测得塔顶A的仰角为45°,在楼顶D处测得塔顶A的仰角为60°,已知地面B处距楼底的距离BC为15米.
(1)求楼高DC.
(2)求铁塔高度(AE的长).
11.如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60°.已知这时气球的高度CD为90米,且点A、D、B在同一直线上.求建筑物A、B间的距离.
12.如图,上空飘着一只气球P,A、B是地面上相距90米的两点,它们分别在气球的正西和正东,测得仰角∠PAB=45°,仰角∠PBA=30°,求气球P的高度(精确到0.1米,≈1.732).
13.如图,某幼儿园将园内滑滑板的倾斜角由45°降为30°,已知原滑道AB的长为5米,点D、B、C在地面同一水平线上.
(l)改善后滑道大约会加长多少米(精确到0.01)?
(2)如果滑滑板的正前方有3米长的空地,就能保证安全,已知原滑道的正前方有6米长的空地,那么像这样改造是否可行?请说明理由.(参考数据:≈1.414,
≈l.732,≈2.449)
14.如图是放置在水平桌面上的台灯的示意图,灯臂AB长为40
cm,灯罩BC长为30
cm,底座厚度为2
cm,灯臂与底座构成的∠BAD=60°,经使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少(精确到0.1
cm,≈1.732)?
15.某水库大坝的横截面是梯形ABCD,AD∥BC,EF为水库的水面,点E在DC上,某课题小组在老师的带领下想测量水的深度,他们测得背水坡AB的长为12米,迎水坡上DE的长为2米,∠BAD=135?,∠ADC=120?,求水深(精确到0.1米,≈1.41,≈1.73).
16.如图,在海面上产生了一股强台风,台风中心(记作点M)位于滨海市(记作点A)的南偏西15?,距离为61千米,且位于临海市(记作点B)的正西方向60千米处.台风中心正以72千米/时的速度沿北偏东60?的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.
(1)滨海市、临海市是否会受到此次台风的侵袭?请说明理由.
(2)若受到此次台风侵袭,该城市受到台风侵袭的持续时间有多少小时?
巩固练习答案:
1.B
2.
3.250
4.B、C两点间的距离为2+2
5.(4+4)
6.C
7.6
8.A
9.C
10.(1)
15米
(2)
15米
11.建筑物A、B间的距离为120米
12.气球P的高度约为32.9米
13.(1)
改善后滑道会加长2.07米
(2)∵
2.588+3<6,∴这样改造可行
14.
此时灯罩顶端C到桌面的高度CE约是51.6
cm
15.水深约为6.7米
16.滨海市不会受到台风的侵袭,临海市会受到台风的侵袭
(2)
临海市会受到台风侵袭的时间为小时
知识梳理:
类型1仰角、俯角:在视线与水平线所成的锐角中,视线在水平线上方的角叫仰角,视线在水平线下方的角叫俯角。
类型2
坡度(坡比):
坡面的铅直高度h和水平宽度l的比叫坡度(坡比),用字母i表示;坡面与水平线的夹角a叫坡角i=tana=
类型3方向角:指北或指南的方向线与目标方向线所成的小于90°的锐角叫做方向角。
注意:东北方向指北偏东45°方向,东南方向指南偏东45°方向,西北方向指北偏西45°方向,西南方向指南偏西45°方向.
例题讲解:
例1.如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号)。
例2.如图,在一个坡角为15°的斜坡上有一棵树,高为AB。当太阳光与水平线成500时,测得该树在斜坡上的树影BC的长为7m,求树高。(精确到0.1m)
例3.要在宽为28m的海堤公路的路边安装路灯。路灯的灯臂长为3m,且与灯柱成120°(如图所示),路灯采用圆锥形灯罩,灯罩的轴线与灯臂垂直。当灯罩的轴线通过公路路面的中线时,照明效果最理想。问:应设计多高的灯柱,才能取得最理想的照明效果?
例4.已知:如图,在△ABC中,∠CAB=120°,AB=4,AC=2,AD⊥BC,D是垂足。求:AD的长。
例5.如图,甲、乙两只捕捞船同时从A港出海捕鱼。甲船以每小时15千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进。甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇。
(1)甲船从C处追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是每小时多少千米?
例6.如图,在A、B两座工厂之间要修建一条笔直的公路,从A地测得B地的走向是南偏东52°,现A、B两地要同时开工,若干天后公路准确对接,则B地所修公路的走向应该是(
)
A北偏西52°
B南偏东52°
C西偏北52°
D北偏西
例7.梯形护坡石坝的斜坡AB的坡度i=1:3,坝高BC为2米,则斜坡AB的长是多少米?坡角为多少度?
例8.如图,在离水面高度为5米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米收绳.问:8秒后船向岸边移动了多少米?(结果精确到0.1米)
例9.据气象台预报,一强台风的中心位于宁波(指城区,下同)东南方向(36)千米的海面上,目前台风中心正以20千米/时的速度向北偏西60°的方向移动,距台风中心50千米的圆形区域均会受到强袭击.已知宁海位于宁波正南方向72千米处,象山位于宁海北偏东60°方向56千米处.请问:宁波、宁海、象山是否会受这次台风的强袭击?如果会,请求出受强袭击的时间;如果不会,请说明理由.
(为解决问题,须画出示意图,现已画出其中一部分,请根据需要,把图形画完整)
巩固练习:
1.如图,先锋村准备在坡角为α的山坡上栽树,如果要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为
(
)
A.5cosa米
B.米
C.5sina米
D.米
2.如图,AB是伸缩式的遮阳棚,CD是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,则AB的长度是______米(假设夏至的正午时刻阳光与地平面的夹角为60°).
3.如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°方向上,在A处正东500米的B处,测得海中灯塔P在北偏东30°方向上,则灯塔P到环海路的距离PC=________米(用根号表示).
4.某校兴趣小组乘坐游轮拍摄海河两岸美景.如图,游轮出发点A与望海楼B的距离为300
m.在A处测得望海楼B位于A的北偏东30°方向,游轮沿正北方向行驶一段时间后到达C,在C处测得望海楼B位于C的北偏东60°方向,求此时游轮与望海楼之间的距离BC的长(≈1.73,结果保留整数).
5.兵兵家的一棵树因台风于A处折断,如图所示,测得树梢触地点B
到树根C处的距离为4米,∠ABC约为45°,树干AC垂直于地面,
那么此树在未折断之前的高度约为________米(答案可保留根号).
6.已知等腰梯形的腰长是4cm,下底长为8
cm,底角的余弦值为,则这个梯形的上底长为(
)
A.8
cm
B.6
cm
C.4
cm
D.2
cm
7.如图,甲、乙为两个高度相等且底面直径之比为1:2的圆柱形水杯,甲杯装满液体,乙杯是空杯.若把甲杯中的液体全部倒入乙杯,则乙杯中的液面与图中点P的距离是________cm.
8.如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5
m(即小颖的眼睛与地面的距离),那么这棵树高
(
)
A.(+)m
B.(5+)m
C.
m
D.4m
9.如图,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,如果这时气球的高度CD为150米,且点A、D、B在同一直线上,那么建筑物A、B间的距离为(
)
A.150米
B.180米
C.200米
D.220米
10.某广电大楼顶部有一发射塔,在地面B处测得楼顶D的仰角为30°,测得塔顶A的仰角为45°,在楼顶D处测得塔顶A的仰角为60°,已知地面B处距楼底的距离BC为15米.
(1)求楼高DC.
(2)求铁塔高度(AE的长).
11.如图,从热气球C上测得两建筑物A、B底部的俯角分别为30°和60°.已知这时气球的高度CD为90米,且点A、D、B在同一直线上.求建筑物A、B间的距离.
12.如图,上空飘着一只气球P,A、B是地面上相距90米的两点,它们分别在气球的正西和正东,测得仰角∠PAB=45°,仰角∠PBA=30°,求气球P的高度(精确到0.1米,≈1.732).
13.如图,某幼儿园将园内滑滑板的倾斜角由45°降为30°,已知原滑道AB的长为5米,点D、B、C在地面同一水平线上.
(l)改善后滑道大约会加长多少米(精确到0.01)?
(2)如果滑滑板的正前方有3米长的空地,就能保证安全,已知原滑道的正前方有6米长的空地,那么像这样改造是否可行?请说明理由.(参考数据:≈1.414,
≈l.732,≈2.449)
14.如图是放置在水平桌面上的台灯的示意图,灯臂AB长为40
cm,灯罩BC长为30
cm,底座厚度为2
cm,灯臂与底座构成的∠BAD=60°,经使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少(精确到0.1
cm,≈1.732)?
15.某水库大坝的横截面是梯形ABCD,AD∥BC,EF为水库的水面,点E在DC上,某课题小组在老师的带领下想测量水的深度,他们测得背水坡AB的长为12米,迎水坡上DE的长为2米,∠BAD=135?,∠ADC=120?,求水深(精确到0.1米,≈1.41,≈1.73).
16.如图,在海面上产生了一股强台风,台风中心(记作点M)位于滨海市(记作点A)的南偏西15?,距离为61千米,且位于临海市(记作点B)的正西方向60千米处.台风中心正以72千米/时的速度沿北偏东60?的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.
(1)滨海市、临海市是否会受到此次台风的侵袭?请说明理由.
(2)若受到此次台风侵袭,该城市受到台风侵袭的持续时间有多少小时?
巩固练习答案:
1.B
2.
3.250
4.B、C两点间的距离为2+2
5.(4+4)
6.C
7.6
8.A
9.C
10.(1)
15米
(2)
15米
11.建筑物A、B间的距离为120米
12.气球P的高度约为32.9米
13.(1)
改善后滑道会加长2.07米
(2)∵
2.588+3<6,∴这样改造可行
14.
此时灯罩顶端C到桌面的高度CE约是51.6
cm
15.水深约为6.7米
16.滨海市不会受到台风的侵袭,临海市会受到台风的侵袭
(2)
临海市会受到台风侵袭的时间为小时
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
