冀教版数学九年级上册第二十五章图形的相似综合测试 (word含答案)
文档属性
| 名称 | 冀教版数学九年级上册第二十五章图形的相似综合测试 (word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 557.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 06:44:51 | ||
图片预览




文档简介
第25章《图形的相似》综合测试
一、选择题
1.已知△ABC∽△A1B1C1,且∠A=55°,∠B1=95°,则∠C等于(
)
A.30°
B.55°
C.95°
D.40°
2.如图1,H为平行四边形ABCD中AD边上一点,且AH=DH,AC和BH交于点K,则AK:KC等于(
)
A.1:2
B.1:1
C.1:3
D.2:3
3.我国国土面积约为960万平方千米,画在比例尺为1:1000万的地图上的面积约是( )
A.960平方千米
B.960平方米
C.960平方分米
D.960平方厘米
4.如图,△ABC中,DE∥AB,则下列式子中错误的是( )
A.
B.
C.
D.
5.下列各组条件中,不能判定△ABC与△A′B′C′相似的是(
)
A.∠A=∠A′,∠B=∠B′
B.∠C=∠C′=90°,∠A=12°,∠B′=78°
C.∠A=∠B,∠B′=∠A′
D.∠A+∠B=∠A′+∠B′,∠A-∠B=∠A′-∠B′
6.已知△ABC∽△A′B′C′且,则为( )
A.1:2
B.2:1
C.1:4
D.4:1
7.如图,在3×3正方形网格中,顶点是网格线的交点的三角形叫做格点三角形,给出下列命题:
①一定存在全等的两个格点三角形
②一定存在相似且不全等的两个格点三角形
③一定存在两个格点三角形是位似图形
④一定存在周长和面积均为无理数的格点三角形
其中真命题的个数是( )
A.4个
B.3个
C.2个
D.1个
8.已知△ABC∽△DEF
,
且△ABC的三边长分别为4,5,6,△DEF的一边长为2,则△DEF的周长为( )
A.7.5
B.6
C.5或6
D.5或6或7.5
9.如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形对应边不成比例的一组是(??
?
)
A.
B.
C.
D.
10.如图,△ABC∽△ACD,相似比为2,则S△BDC:S△DAC为(
)
A.4:1
B.3:1
C.2:1
D.1:1
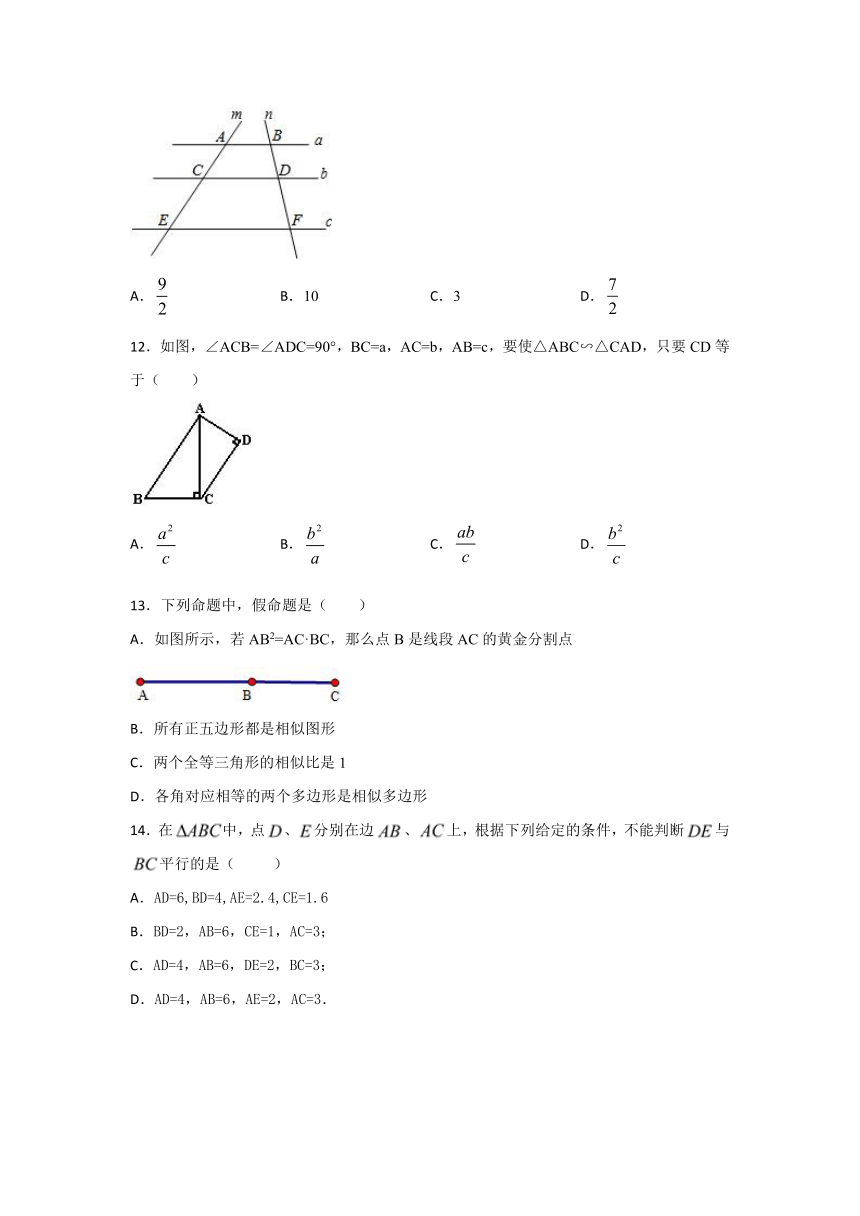
11.如图,直线a∥b∥c,直线m,n与a,b,c分别相交于点A,C,E和点B,D,
F,若AC=4,AE=10,BF=,则DF的长为(
)
A.
B.10
C.3
D.
12.如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使△ABC∽△CAD,只要CD等于( )
A.
B.
C.
D.
13.下列命题中,假命题是( )
A.如图所示,若AB2=AC·BC,那么点B是线段AC的黄金分割点
B.所有正五边形都是相似图形
C.两个全等三角形的相似比是1
D.各角对应相等的两个多边形是相似多边形
14.在中,点、分别在边、上,根据下列给定的条件,不能判断与平行的是(
)
A.AD=6,BD=4,AE=2.4,CE=1.6
B.BD=2,AB=6,CE=1,AC=3;
C.AD=4,AB=6,DE=2,BC=3;
D.AD=4,AB=6,AE=2,AC=3.
15.如图所示:∠CAB=∠BCD,AD=2,BD=4,则BC=(
)
A.
B.
C.3
D.6
16.如图所示为农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE的长为1米,支撑点A到踏脚D的距离为0.6米,原来捣头点E着地,现在踏脚D着地,则捣头点E上升了( )
.0.5米
B.0.6米
C.0.3米
D.0.9米
17.如图,在平行四边形ABCD中AE:EB=1:2
,
S?AEF=3,
则S?FCD为(
)
A.3
B.27
C.6
D.12
18.如图,正方形ABCD中,E是CD的中点,P是BC边上的一点,下列条件中,不能推出△ABP和△ECP相似的是( )
A.∠APB=∠EPC
B.∠APE=90°
C.BP:BC=2:3
D.P是BC中点
19.如图,在中,,分别交,于点,.若,,则的面积与的面积的比等于(
)
A.
B.
C.
D.
20.如图,下列条件不能判定△ABC与△ADE相似的是
A.
B.∠B=∠ADE
C.∠C=∠AED
D.
21.如图,四边形和是以点为位似中心的位似图形,若,则四边形与四边形的面积比为(
)
A.4:9
B.2:5
C.2:3
D.
二、填空题
22.两个相似三角形,已知其中一个三角形的边分别为4、5、6,另一个三角形的一边长为2,求另一个三角形的最长边____________________.
23.已知△ABC∽△A`B`C`,且BC:B`C`=3:2,△ABC的周长为24,则△A`B`C`的周长为_______.
24.如图,在△ABC中,点P是AC上一点,连接BP.要使△ABP∽△ACB,则必须有∠ABP=_____.
25.△ABC与△A′B′C′是位似图形,且△ABC与△的位似比是1:2,已知△ABC的面积是3,则△的面积是________
26.如图,AB//CD,AD与BC相交于点E,如果AB=2,CD=6,AE=1,那么
DE=
_________.
27.如图,AD∥EF∥BC,,DF=6cm,则DC=_________cm.
28.已知如图,梯形中,,△COD与△AOB的周长比为1∶2,则
:
=
_______.
29.如图,梯形
ABCD中,AD∥BC∥EF,
AE∶EB=2∶3,
AD=12,则BC=18,则EF=____
30.有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2=________.
31.如图,△ABC中有菱形AMPN,如果=,那么=_____.
32.若点C是线段AB的黄金分割点,则等于__.
33.如图,四边形与四边形相似,位似中心点是,,则
.
34.如图所示,在正方形ABCD中,点E是BC边上一点,且BE:EC=2:1,AE与BD交于点F,则△AFD与四边形DFEC的面积之比是________.
35.如图,已知中,=8,=6,点是线段的中点,点在线段上,且∽,则=
_________;
36.如图,晚上,小亮走在大街上,他发现:当他站在大街两边的两盏路灯(AB和EC)之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子HN长为3
m,左边的影子FH长为1m.小亮身高GH为1.5m,两盏路灯的高相同,两盏路灯之间的距离BC为16m,则路灯的高为____
m;
三、解答题
37.如图,在和中,,为线段上一点,且.,,,求的长.
38.如图,,,,,.试说明:
39.如图,在Rt△ABC中,∠ACB=90,CDAB于D.
(1)写出图中相似的三角形;
(2)求证:=
AD·BD
.
40.如图,已知AD=2,DB=1,∠ACD
=∠B,∠BAC的平分线分别交CD、BC于F、E.
(1)求AC的值
(2)求的值.
41.已知:如图,在△ABC中,∠ACB的平分线CD交AB于D,过B作BE∥CD交
AC的延长线于点E.
(1)求证:BC
=
CE;
(2)求证:
42.已知:如图,F是四边形ABCD对角线AC上一点,EF∥BC,FG∥AD.
求证:+=1
43.如图,D、E分别是△ABC的边BC、AB上的点,△ABC,△BDE,△ACD的周长依次为,,.
(1)当∠2=∠3,BD=BC时,求的值;
(2)当∠1=∠2,BD=BC时,求的值;
(3)当∠1=∠2=∠3时,证明:≤.
44.如图,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA向点A匀速运动,速度均为3cm/s;同时点Q由A出发沿AC向点C匀速运动,速度为2cm/s.当一点到达终点,另一点就停止运动;连接PQ,设运动的时间为t
s.
(1)当t为何值时,PQ∥BC.
(2)设△AQP的面积为S(单位:cm2),写出S与t的函数关系式,并写出自变量的取值范围.
(3)是否存在某时刻的t值,使线段PQ恰好把△ABC的面积分为1:4两部分?若存
在,求出此时t的值;若不存在,请说明理由.
参考答案
1-5.ACDCC
6-10.CBDDB
11-15.ADDCB
16-21.ABDDDA
22.2、3、
23.16
24.∠ABP=∠C或∠APB=∠ABC或
25.12
26.3
27.15
28.2:1
29.14.4
30.4:9.
31.
32.或
33.
34.9:11
35.;
36.7.5;
37.1.
38.解:∵AC=6,AB=12,AE=4,AF=8,
∴=2,
∵∠1=∠2,
∴△ACE∽△ABF,
∴∠ACE=∠ABF.
39.解:(1)∵∠ACB=90°,CD⊥AB,∴∠A+∠B=∠BCD+∠B,∴∠A=∠BCD,且∠ADC=∠CDB,∴△ADC∽△CDB,在△ADC和△ACB中,∠A=∠A,∠ADC=∠ACB,∴△ADC∽△ACB,同理可得△CDB∽△ACB,∴图中所有相似的三角形有:
△ADC∽△CDB,△ADC∽△ACB,△CDB∽△ACB;
(2)∵△ADC∽△CDB,∴,∴CD2=AD?DB.
40.(1)(2)
41.证明:(1)∵CD平分∠ACB,
∴∠ACD=∠BCD.
又∵BE∥CD,
∴∠CBE=∠BCD,∠CEB=∠ACD.
∵∠ACD=∠BCD,
∴∠CBE=∠CEB.
故△BCE是等腰三角形,BC=CE.
(2)∵BE∥CD,根据平行线分线段成比例定理可得=,
又∵BC=CE,
∴=.
42.∵EF∥BC,
∴
∵FG∥AD,
∴
43.(1)∵∠2=∠3,∴DE∥AC,
∴△BDE∽△BCA
∴=,
由BD=BC,得=,
即=;
(2)∵∠1=∠2,∠C是公共角,
∴△ACD∽△BCA,
∴==
∴==,
由BD=BC,得DC=BC,
∴=;
(3)由∠2=∠3,得DE∥AC,
∴△BDE∽△BCA;
∠1=∠2,∠C是公共角,∴△ACD∽△BCA,
∴△ACD∽△BDE∽△BCA.
∴=
①
== ②
由②得,==
==1-=1-,
∴=1-.
=+=1-+
=-++1=-,
∵-≤0,
∴≤.
44.(1)当t为s时,PQ∥BC;(2)S=t2+6t
,自变量t的取值范围是0
一、选择题
1.已知△ABC∽△A1B1C1,且∠A=55°,∠B1=95°,则∠C等于(
)
A.30°
B.55°
C.95°
D.40°
2.如图1,H为平行四边形ABCD中AD边上一点,且AH=DH,AC和BH交于点K,则AK:KC等于(
)
A.1:2
B.1:1
C.1:3
D.2:3
3.我国国土面积约为960万平方千米,画在比例尺为1:1000万的地图上的面积约是( )
A.960平方千米
B.960平方米
C.960平方分米
D.960平方厘米
4.如图,△ABC中,DE∥AB,则下列式子中错误的是( )
A.
B.
C.
D.
5.下列各组条件中,不能判定△ABC与△A′B′C′相似的是(
)
A.∠A=∠A′,∠B=∠B′
B.∠C=∠C′=90°,∠A=12°,∠B′=78°
C.∠A=∠B,∠B′=∠A′
D.∠A+∠B=∠A′+∠B′,∠A-∠B=∠A′-∠B′
6.已知△ABC∽△A′B′C′且,则为( )
A.1:2
B.2:1
C.1:4
D.4:1
7.如图,在3×3正方形网格中,顶点是网格线的交点的三角形叫做格点三角形,给出下列命题:
①一定存在全等的两个格点三角形
②一定存在相似且不全等的两个格点三角形
③一定存在两个格点三角形是位似图形
④一定存在周长和面积均为无理数的格点三角形
其中真命题的个数是( )
A.4个
B.3个
C.2个
D.1个
8.已知△ABC∽△DEF
,
且△ABC的三边长分别为4,5,6,△DEF的一边长为2,则△DEF的周长为( )
A.7.5
B.6
C.5或6
D.5或6或7.5
9.如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形对应边不成比例的一组是(??
?
)
A.
B.
C.
D.
10.如图,△ABC∽△ACD,相似比为2,则S△BDC:S△DAC为(
)
A.4:1
B.3:1
C.2:1
D.1:1
11.如图,直线a∥b∥c,直线m,n与a,b,c分别相交于点A,C,E和点B,D,
F,若AC=4,AE=10,BF=,则DF的长为(
)
A.
B.10
C.3
D.
12.如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使△ABC∽△CAD,只要CD等于( )
A.
B.
C.
D.
13.下列命题中,假命题是( )
A.如图所示,若AB2=AC·BC,那么点B是线段AC的黄金分割点
B.所有正五边形都是相似图形
C.两个全等三角形的相似比是1
D.各角对应相等的两个多边形是相似多边形
14.在中,点、分别在边、上,根据下列给定的条件,不能判断与平行的是(
)
A.AD=6,BD=4,AE=2.4,CE=1.6
B.BD=2,AB=6,CE=1,AC=3;
C.AD=4,AB=6,DE=2,BC=3;
D.AD=4,AB=6,AE=2,AC=3.
15.如图所示:∠CAB=∠BCD,AD=2,BD=4,则BC=(
)
A.
B.
C.3
D.6
16.如图所示为农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE的长为1米,支撑点A到踏脚D的距离为0.6米,原来捣头点E着地,现在踏脚D着地,则捣头点E上升了( )
.0.5米
B.0.6米
C.0.3米
D.0.9米
17.如图,在平行四边形ABCD中AE:EB=1:2
,
S?AEF=3,
则S?FCD为(
)
A.3
B.27
C.6
D.12
18.如图,正方形ABCD中,E是CD的中点,P是BC边上的一点,下列条件中,不能推出△ABP和△ECP相似的是( )
A.∠APB=∠EPC
B.∠APE=90°
C.BP:BC=2:3
D.P是BC中点
19.如图,在中,,分别交,于点,.若,,则的面积与的面积的比等于(
)
A.
B.
C.
D.
20.如图,下列条件不能判定△ABC与△ADE相似的是
A.
B.∠B=∠ADE
C.∠C=∠AED
D.
21.如图,四边形和是以点为位似中心的位似图形,若,则四边形与四边形的面积比为(
)
A.4:9
B.2:5
C.2:3
D.
二、填空题
22.两个相似三角形,已知其中一个三角形的边分别为4、5、6,另一个三角形的一边长为2,求另一个三角形的最长边____________________.
23.已知△ABC∽△A`B`C`,且BC:B`C`=3:2,△ABC的周长为24,则△A`B`C`的周长为_______.
24.如图,在△ABC中,点P是AC上一点,连接BP.要使△ABP∽△ACB,则必须有∠ABP=_____.
25.△ABC与△A′B′C′是位似图形,且△ABC与△的位似比是1:2,已知△ABC的面积是3,则△的面积是________
26.如图,AB//CD,AD与BC相交于点E,如果AB=2,CD=6,AE=1,那么
DE=
_________.
27.如图,AD∥EF∥BC,,DF=6cm,则DC=_________cm.
28.已知如图,梯形中,,△COD与△AOB的周长比为1∶2,则
:
=
_______.
29.如图,梯形
ABCD中,AD∥BC∥EF,
AE∶EB=2∶3,
AD=12,则BC=18,则EF=____
30.有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2=________.
31.如图,△ABC中有菱形AMPN,如果=,那么=_____.
32.若点C是线段AB的黄金分割点,则等于__.
33.如图,四边形与四边形相似,位似中心点是,,则
.
34.如图所示,在正方形ABCD中,点E是BC边上一点,且BE:EC=2:1,AE与BD交于点F,则△AFD与四边形DFEC的面积之比是________.
35.如图,已知中,=8,=6,点是线段的中点,点在线段上,且∽,则=
_________;
36.如图,晚上,小亮走在大街上,他发现:当他站在大街两边的两盏路灯(AB和EC)之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子HN长为3
m,左边的影子FH长为1m.小亮身高GH为1.5m,两盏路灯的高相同,两盏路灯之间的距离BC为16m,则路灯的高为____
m;
三、解答题
37.如图,在和中,,为线段上一点,且.,,,求的长.
38.如图,,,,,.试说明:
39.如图,在Rt△ABC中,∠ACB=90,CDAB于D.
(1)写出图中相似的三角形;
(2)求证:=
AD·BD
.
40.如图,已知AD=2,DB=1,∠ACD
=∠B,∠BAC的平分线分别交CD、BC于F、E.
(1)求AC的值
(2)求的值.
41.已知:如图,在△ABC中,∠ACB的平分线CD交AB于D,过B作BE∥CD交
AC的延长线于点E.
(1)求证:BC
=
CE;
(2)求证:
42.已知:如图,F是四边形ABCD对角线AC上一点,EF∥BC,FG∥AD.
求证:+=1
43.如图,D、E分别是△ABC的边BC、AB上的点,△ABC,△BDE,△ACD的周长依次为,,.
(1)当∠2=∠3,BD=BC时,求的值;
(2)当∠1=∠2,BD=BC时,求的值;
(3)当∠1=∠2=∠3时,证明:≤.
44.如图,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA向点A匀速运动,速度均为3cm/s;同时点Q由A出发沿AC向点C匀速运动,速度为2cm/s.当一点到达终点,另一点就停止运动;连接PQ,设运动的时间为t
s.
(1)当t为何值时,PQ∥BC.
(2)设△AQP的面积为S(单位:cm2),写出S与t的函数关系式,并写出自变量的取值范围.
(3)是否存在某时刻的t值,使线段PQ恰好把△ABC的面积分为1:4两部分?若存
在,求出此时t的值;若不存在,请说明理由.
参考答案
1-5.ACDCC
6-10.CBDDB
11-15.ADDCB
16-21.ABDDDA
22.2、3、
23.16
24.∠ABP=∠C或∠APB=∠ABC或
25.12
26.3
27.15
28.2:1
29.14.4
30.4:9.
31.
32.或
33.
34.9:11
35.;
36.7.5;
37.1.
38.解:∵AC=6,AB=12,AE=4,AF=8,
∴=2,
∵∠1=∠2,
∴△ACE∽△ABF,
∴∠ACE=∠ABF.
39.解:(1)∵∠ACB=90°,CD⊥AB,∴∠A+∠B=∠BCD+∠B,∴∠A=∠BCD,且∠ADC=∠CDB,∴△ADC∽△CDB,在△ADC和△ACB中,∠A=∠A,∠ADC=∠ACB,∴△ADC∽△ACB,同理可得△CDB∽△ACB,∴图中所有相似的三角形有:
△ADC∽△CDB,△ADC∽△ACB,△CDB∽△ACB;
(2)∵△ADC∽△CDB,∴,∴CD2=AD?DB.
40.(1)(2)
41.证明:(1)∵CD平分∠ACB,
∴∠ACD=∠BCD.
又∵BE∥CD,
∴∠CBE=∠BCD,∠CEB=∠ACD.
∵∠ACD=∠BCD,
∴∠CBE=∠CEB.
故△BCE是等腰三角形,BC=CE.
(2)∵BE∥CD,根据平行线分线段成比例定理可得=,
又∵BC=CE,
∴=.
42.∵EF∥BC,
∴
∵FG∥AD,
∴
43.(1)∵∠2=∠3,∴DE∥AC,
∴△BDE∽△BCA
∴=,
由BD=BC,得=,
即=;
(2)∵∠1=∠2,∠C是公共角,
∴△ACD∽△BCA,
∴==
∴==,
由BD=BC,得DC=BC,
∴=;
(3)由∠2=∠3,得DE∥AC,
∴△BDE∽△BCA;
∠1=∠2,∠C是公共角,∴△ACD∽△BCA,
∴△ACD∽△BDE∽△BCA.
∴=
①
== ②
由②得,==
==1-=1-,
∴=1-.
=+=1-+
=-++1=-,
∵-≤0,
∴≤.
44.(1)当t为s时,PQ∥BC;(2)S=t2+6t
,自变量t的取值范围是0
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
