鲁教版九年级数学上册 第一章 反比例函数 复习学案(word版无答案)
文档属性
| 名称 | 鲁教版九年级数学上册 第一章 反比例函数 复习学案(word版无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 170.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 00:00:00 | ||
图片预览

文档简介
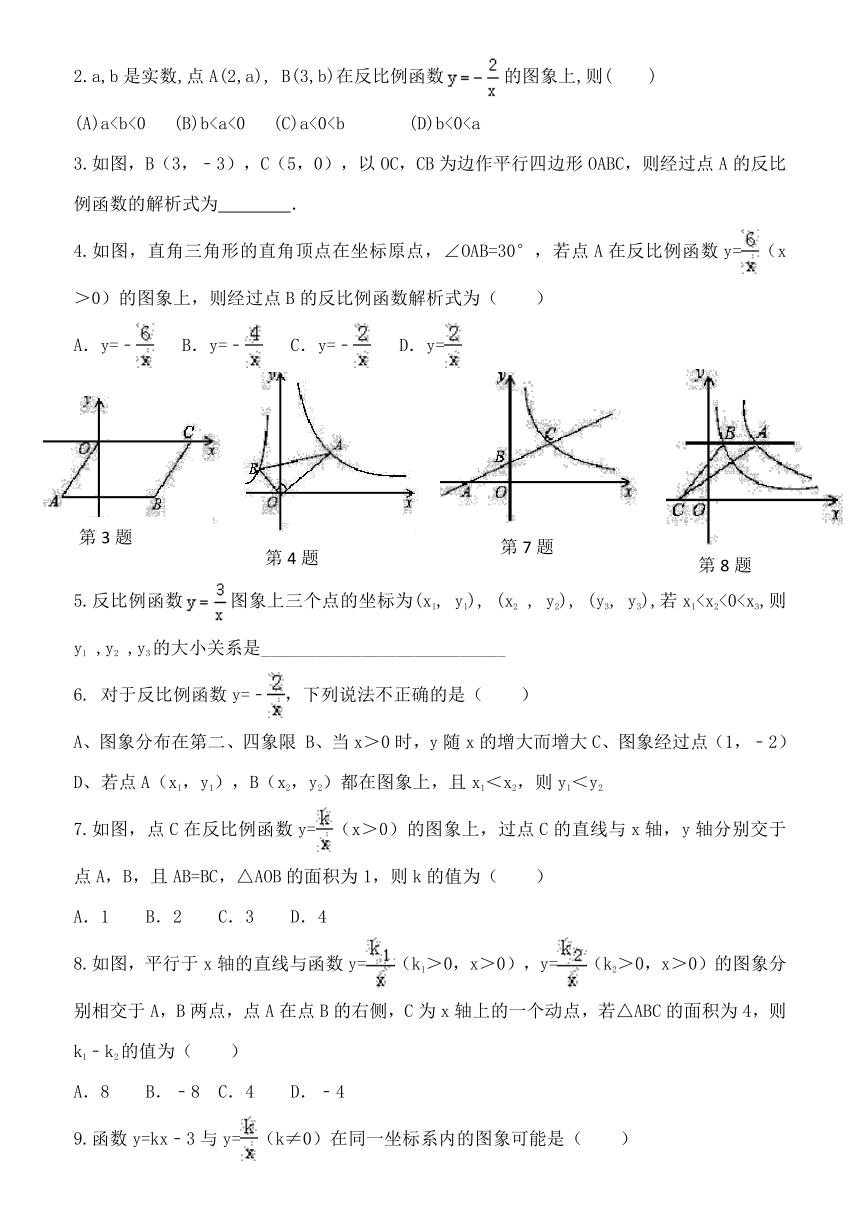
反比例函数复习导学案
班级:__________
姓名:__________
【知识梳理】
概念
一般地,如果两个变量x,y之间的关系可以表示成__________(k为常数,k≠0)的形式,,那么称y是x的反比例函数.
常用形式
__________
②__________
③__________
k的符号
k>0
k<0
图象
性质
此时函数图象的两个分支分别在______象限。在每个象限内,y随x的增大而_______。
此时函数图象的两个分以分别在______象限。在每个象限内,y随x的增大而_______。
反比例函数的几何意义
设点P(x,y)是反比例函数图象上一点,过点P作x轴、y轴的垂线,垂足分别为M、N,则矩形PNOM的面积等于___________;连接OP,则三角形POM的面积等于__________.
下列函数中,反比例函数是(
).
A.y=
—
C.y=
—x+7
D.y=
—x2
—1
2.a,b是实数,点A(2,a),
B(3,b)在反比例函数的图象上,则(
)
(A)a(B)b(C)a<0(D)b<03.如图,B(3,﹣3),C(5,0),以OC,CB为边作平行四边形OABC,则经过点A的反比例函数的解析式为
.
4.如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=(x>0)的图象上,则经过点B的反比例函数解析式为( )
A.y=﹣
B.y=﹣
C.y=﹣
D.y=
5.反比例函数图象上三个点的坐标为(x1,
y1),
(x2
,
y2),
(y3,
y3),若x1,y2
,y3的大小关系是___________________________
6.
对于反比例函数y=﹣,下列说法不正确的是( )
A、图象分布在第二、四象限
B、当x>0时,y随x的增大而增大C、图象经过点(1,﹣2)
D、若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y2
7.如图,点C在反比例函数y=(x>0)的图象上,过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,则k的值为( )
A.1
B.2
C.3
D.4
8.如图,平行于x轴的直线与函数y=(k1>0,x>0),y=(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为4,则k1﹣k2的值为( )
A.8
B.﹣8
C.4
D.﹣4
9.函数y=kx﹣3与y=(k≠0)在同一坐标系内的图象可能是( )
A.
B.
C.
D.
10.直线y=kx(k>0)与双曲线交于两点,则的值为___
11.如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤的解集.
12.如图,一次函数y=x+4的图象与反比例函数y=(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=S△BOC,求点P的坐标.
13.如图,已知点D在反比例函数y=的图象上,过点D作DB⊥y轴,垂足为B(0,3),直线y=kx+b经过点A(5,0),与y轴交于点C,且BD=OC,OC:OA=2:5.
(1)求反比例函数y=和一次函数y=kx+b的表达式;
(2)直接写出关于x的不等式>kx+b的解集.
第8题
第4题
第7题
第3题
班级:__________
姓名:__________
【知识梳理】
概念
一般地,如果两个变量x,y之间的关系可以表示成__________(k为常数,k≠0)的形式,,那么称y是x的反比例函数.
常用形式
__________
②__________
③__________
k的符号
k>0
k<0
图象
性质
此时函数图象的两个分支分别在______象限。在每个象限内,y随x的增大而_______。
此时函数图象的两个分以分别在______象限。在每个象限内,y随x的增大而_______。
反比例函数的几何意义
设点P(x,y)是反比例函数图象上一点,过点P作x轴、y轴的垂线,垂足分别为M、N,则矩形PNOM的面积等于___________;连接OP,则三角形POM的面积等于__________.
下列函数中,反比例函数是(
).
A.y=
—
C.y=
—x+7
D.y=
—x2
—1
2.a,b是实数,点A(2,a),
B(3,b)在反比例函数的图象上,则(
)
(A)a
.
4.如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=(x>0)的图象上,则经过点B的反比例函数解析式为( )
A.y=﹣
B.y=﹣
C.y=﹣
D.y=
5.反比例函数图象上三个点的坐标为(x1,
y1),
(x2
,
y2),
(y3,
y3),若x1
,y3的大小关系是___________________________
6.
对于反比例函数y=﹣,下列说法不正确的是( )
A、图象分布在第二、四象限
B、当x>0时,y随x的增大而增大C、图象经过点(1,﹣2)
D、若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y2
7.如图,点C在反比例函数y=(x>0)的图象上,过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,则k的值为( )
A.1
B.2
C.3
D.4
8.如图,平行于x轴的直线与函数y=(k1>0,x>0),y=(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为4,则k1﹣k2的值为( )
A.8
B.﹣8
C.4
D.﹣4
9.函数y=kx﹣3与y=(k≠0)在同一坐标系内的图象可能是( )
A.
B.
C.
D.
10.直线y=kx(k>0)与双曲线交于两点,则的值为___
11.如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤的解集.
12.如图,一次函数y=x+4的图象与反比例函数y=(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=S△BOC,求点P的坐标.
13.如图,已知点D在反比例函数y=的图象上,过点D作DB⊥y轴,垂足为B(0,3),直线y=kx+b经过点A(5,0),与y轴交于点C,且BD=OC,OC:OA=2:5.
(1)求反比例函数y=和一次函数y=kx+b的表达式;
(2)直接写出关于x的不等式>kx+b的解集.
第8题
第4题
第7题
第3题
