人教A版(2019)必修第一册第三章函数的概念与性质 3.4.2用二分法求方程的近似解-课件(共27张PPT)
文档属性
| 名称 | 人教A版(2019)必修第一册第三章函数的概念与性质 3.4.2用二分法求方程的近似解-课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 882.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 10:16:21 | ||
图片预览






文档简介
用二分法求方程的近似解
引入问题,探讨方法.
函数零点
存在定理
函数
单调性
函数零点个数
方程实数解的个数
利用函数研究方程的近似解.
上节课
?
?
?
?
本节课
问题1:我们已经知道函数 f?x?=?lnx+2x?6在(2,3) 内存在一个零点,如何求出这个零点?
?
引入问题,探讨方法.
追问1:你能求出函数?f?x?=?lnx+2x?6零点的精确值吗?
?
只需求出满足一定精确度的近似解.
例如:当精确度为????时,只需|近似值?精确值| ?
问题1:我们已经知道函数?f?x?=?lnx+2x?6在(2,3)内存在一个零点,如何求出这个零点?
?
引入问题,探讨方法.
追问2:当精确度为0.5时,你能得到一个符合要求的零点的近似值吗?
|近似值?精确值| <0.5.
?
x0
2.5
0.5
0.5
1
2.5到零点
x0的距离
<0.5
?
2.5
为区间?(a,b)?的中点.
?
a+b2
?
|2.5? x0| <0.5.
?
问题1:我们已经知道函数?f?x?=?lnx+2x?6在(2,3)内存在一个零点,如何求出这个零点?
?
引入问题,探讨方法.
追问3:当精确度为0.5时,3可以看作零点的一个近似值吗?为什么?
零点x0在(2,2.5)内还是(2.5,3) 内?如何确定?
?
f?2?f?(2.5)
?
f?2.5?f?(3)
?
可以
x0
2.5
0.5
0.5
1
f?2<0
?
f?3>0
?
f?2.5
?
≈?0.084
?
零点x0∈(2.5,3).
?
|3? x0| <0.5.
?
<0
?
问题1:我们已经知道函数?f?x?=?lnx+2x?6在(2,3)内存在一个零点,如何求出这个零点?
?
引入问题,探讨方法.
追问4:当精确度缩小到0.01时,为了得到函数零点的近似值,至少需要将零点所
在区间缩小到什么程度?
我们可以采取怎样的办法来
逐步缩小零点所在区间?
x0
2.5
0.5
0.5
1
区间长度<0.01.
?
重复计算区间中点和区间端点函数值乘积的符号.
x
d < 0.01
a
b
x0
小于0.01
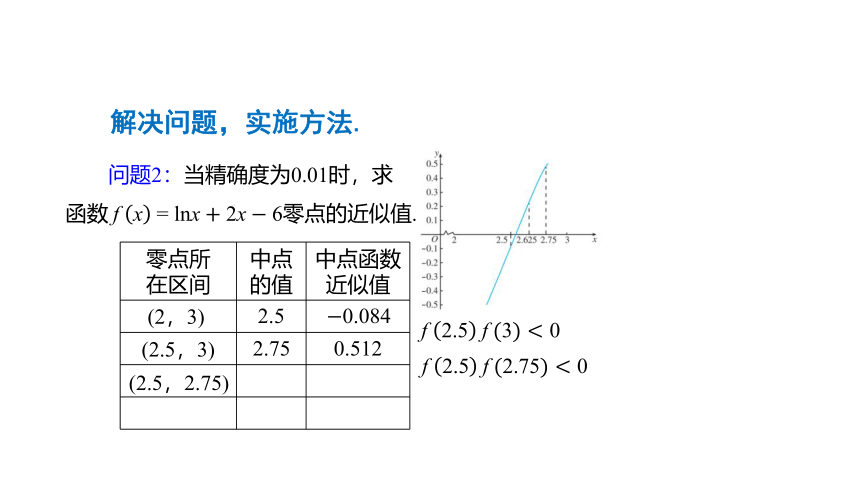
问题2:当精确度为0.01时,求
函数?f?x?=?lnx+2x?6零点的近似值.
?
解决问题,实施方法.
{5940675A-B579-460E-94D1-54222C63F5DA}零点所
在区间
中点
的值
中点函数
近似值
(2,3)
2.5
?0.084
?
f?2.5?f?(3)<0
?
(2.5,3)
2.75
0.512
f?2.5?f?(2.75)<0
?
(2.5,2.75)
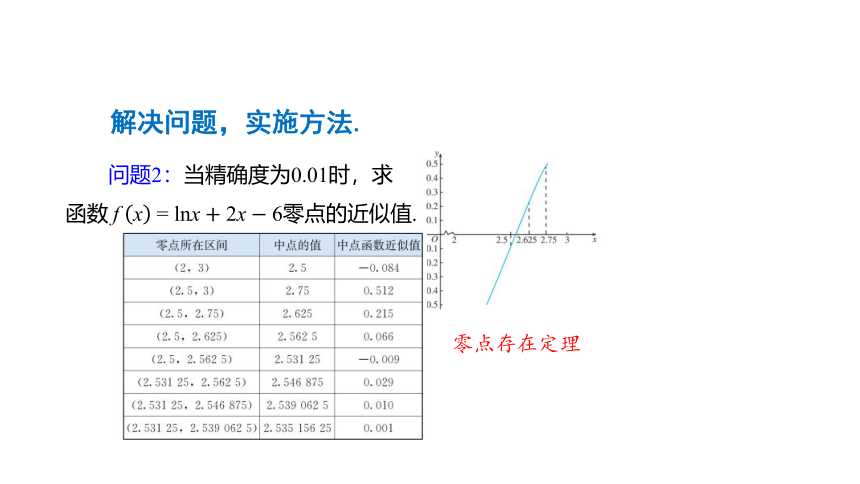
问题2:当精确度为0.01时,求
函数?f?x?=?lnx+2x?6零点的近似值.
?
解决问题,实施方法.
零点存在定理
问题2:当精确度为0.01时,求
函数?f?x?=?lnx+2x?6零点的近似值.
?
解决问题,实施方法.
区间长度<0.01
?
该区间内任意一个数都可以作为零点的近似值.
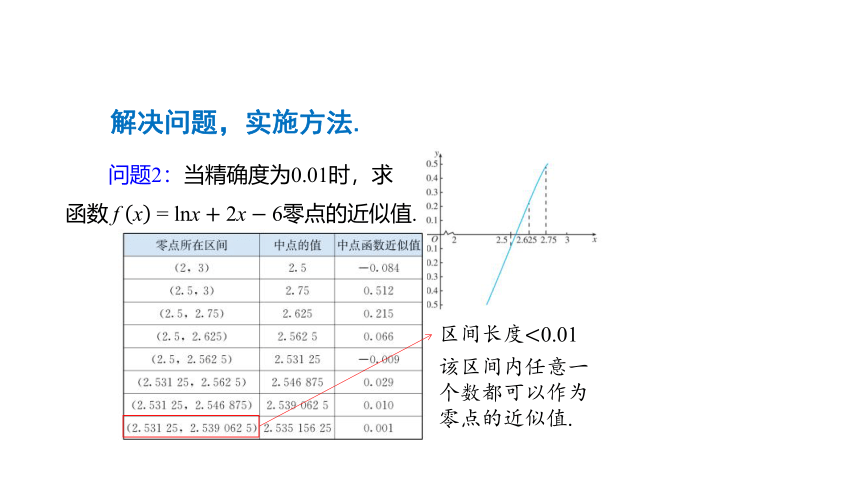
问题2:当精确度为0.01时,求
函数?f?x?=?lnx+2x?6零点的近似值.
?
解决问题,实施方法.
区间长度<0.01
?
为了方便,可以把区间端点作为零点的近似值.
近似值x =?2.53125或2.5390625.
?
方程?lnx+2x?6?=?0的近似解.
?
问题3:在问题2中,我们用怎样
的方法求函数?f?x?=?lnx+2x?6零点
的近似值?这种方法适用于哪些函数?
?
总结提炼,归纳方法.
不断将零点所在区间一分为二,使得区间的两个端点逐步逼近零点.
理论基础:零点存在定理.
适用条件:某区间上图象连续不断,区间端点函
数值的乘积符号为负.
问题3:在问题2中,我们用怎样
的方法求函数?f?x?=?lnx+2x?6零点
的近似值?这种方法适用于哪些函数?
?
总结提炼,归纳方法.
归纳出二分法的定义:
对于在区间[a,b]上图象连续不断且 f?a?f?(b)<0
的函数?y?=?f?x?,通过不断地把它的零点所在区间一分为二,使所得区间的两个端点逐步逼近零点,进而
得到零点近似值的方法叫做二分法.
?
问题4:根据求函数?f?x?=?lnx+2x?6?零点的近似值的过程,你能提炼出给定精确度????,用二分法求函数?y?=?f?x?零点????0的近似值的一般步骤吗?
?
总结提炼,归纳方法.
回顾求函数?f?x?=?lnx+2x?6
零点x0的近似值的过程:
?
总结提炼,归纳方法.
1. 确定初始区间.
f?2?f?(3)<0?x0?∈ (2,3) .
?
回顾求函数?f?x?=?lnx+2x?6
零点x0的近似值的过程:
?
总结提炼,归纳方法.
2. 不断缩小区间
通过重复计算区间中点和区间端点函数值乘积的符号,将零点所在区间逐次减半地缩小.
(1)计算区间中点;
(2)计算中点函数值;
(3)计算区间中点和区间端点函数值乘积的符号;
(4)确定零点所在区间.
区间长度<精确度时结束重复操作.
?
回顾求函数?f?x?=?lnx+2x?6
零点x0的近似值的过程:
?
总结提炼,归纳方法.
1. 确定初始区间.
2. 不断缩小区间.
3. 得到近似值.
f?2?f?(3)<0?x0?∈ (2,3) .
?
通过重复计算区间重点中点和区间端点函数值乘积的符号,将零点所在区间逐次减半地缩小.
当零点所在区间的长度小于精确度时,把区间的一
个端点作为零点的近似值.
总结提炼,归纳方法.
小结:给定精确度????,用二分法求函数?y?=?f?x?零点 x0 的近似值的一般步骤.
?
1. 确定零点 x0 的初始区间[a,b],验证 f?a?f?(b)<0.
?
2. 求区间 (a,b) 的中点c.
3. 计算 f (c),并进一步确定零点所在的区间:
(1)若 f (c)?= 0 (此时 x0?=????),则????就是函数的零点;
(2)若f?a?f?(c)<0 (此时 x0?∈?(a,c) ),则令b?= c;
(3)若f?c?f?(b)<0 (此时 x0?∈?(c,b) ),则令a?= c.
?
4. 判断是否达到精确度????:若| a???b | 近似值a (或 b );否则重复步骤2~4.
?
例题实践,熟悉方法.
问题5:借助信息技术,用二分法求方程
2x+3x?7=0的近似解(精确度为0.1).
?
分析:转化为研究函数 f (x)?=2x+3x?7
零点的近似值(精确度为0.1).
?
f?1?f?(2)<0,
?
说明该函数在区间 (1,2) 内存在零点 x0.
第1步:确定零点 x0 所在的初始区间.
例题实践,熟悉方法.
问题5:借助信息技术,用二分法求方程
2x+3x?7=0的近似解(精确度为0.1).
?
分析:转化为研究函数 f (x)?=2x+3x?7
零点的近似解(精确度为0.1).
?
(1,2).
第1步:确定零点 x0 所在的初始区间.
第2步:求区间中点.
取 (1,2) 的中点 x1 =1.5.
?
例题实践,熟悉方法.
问题5:借助信息技术,用二分法求方程
2x+3x?7=0的近似解(精确度为0.1).
?
分析:转化为研究函数 f (x)?=2x+3x?7
零点的近似解(精确度为0.1).
?
(1,2).
第1步:确定零点 x0 所在的初始区间.
第2步:求区间中点.
取 (1,2) 的中点 x1 =1.5.
?
第3步:计算中点函数值,进一步确定零点
所在区间.
f?1.5≈0.33,
?
所以 f?1?f?(1.5)<0,所以 x0 ∈(1,1.5).
?
f?1<0,
?
例题实践,熟悉方法.
问题5:借助信息技术,用二分法求方程
2x+3x?7=0的近似解(精确度为0.1).
?
分析:转化为研究函数 f (x)?=2x+3x?7
零点的近似解(精确度为0.1).
?
(1,2).
第1步:确定零点 x0 所在的初始区间.
第2步:求区间中点.
取 (1,2) 的中点 x1 =1.5.
?
第3步:计算中点函数值,进一步确定零点
所在区间.
f?1?f?(1.5)<0?x0 ∈(1,1.5).
?
第4步:判断是否达到精确度0.1.
|1.5?1|=0.5>0.1
?
没有达到.
重复步骤2~4.
例题实践,熟悉方法.
问题5:借助信息技术,用二分法求方程
2x+3x?7=0的近似解(精确度为0.1).
?
分析:转化为研究函数 f (x)?=2x+3x?7
零点的近似解(精确度为0.1).
?
……
第2步:求区间中点.
取 (1,1.5) 的中点 x2 =1.25.
?
第3步:计算中点函数值,进一步确定零点所在区间.
f?1.25≈?0.87,
?
因为 f?1.25?f?(1.5)<0,
所以 x0 ∈(1.25,1.5).
?
例题实践,熟悉方法.
问题5:借助信息技术,用二分法求方程
2x+3x?7=0的近似解(精确度为0.1).
?
分析:转化为研究函数 f (x)?=2x+3x?7
零点的近似解(精确度为0.1).
?
……
第2步:求区间中点.
取 (1,1.5) 的中点 x2 =1.25.
?
第3步:计算中点函数值,进一步确定零点所在区间.
f?1.25?f?(1.5)<0?x0 ∈(1.25,1.5).
?
第4步:判断是否达到精确度0.1.
没有达到.
重复步骤2~4.
例题实践,熟悉方法.
问题5:借助信息技术,用二分法求方程
2x+3x?7=0的近似解(精确度为0.1).
?
分析:转化为研究函数 f (x)?=2x+3x?7
零点的近似解(精确度为0.1).
?
……
第2步:求区间中点.
取 (1,1.5) 的中点 x2 =1.25.
?
第3步:计算中点函数值,进一步确定零点所在区间.
f?1.25?f?(1.5)<0?x0 ∈(1.25,1.5).
?
第4步:判断是否达到精确度0.1.
没有达到.
同理可得,x0 ∈(1.375,1.5) ,x0 ∈(1.375,1.4375).
?
例题实践,熟悉方法.
问题5:借助信息技术,用二分法求方程
2x+3x?7=0的近似解(精确度为0.1).
?
分析:转化为研究函数 f (x)?=2x+3x?7
零点的近似解(精确度为0.1).
?
……
同理可得,x0 ∈(1.375,1.5) ,x0 ∈(1.375,1.4375).
?
由于|1.375 ? 1.4375| = 0.0625 < 0.1,所以原方程的近似解可取为1.375(或1.4375).
?
执行“二分法”的实施步骤.
课堂小结
用二分法求方程的近似解
函数零点
方程的解
?
?
不断缩小零点所在区间
函数思想
极限思想
算法思想
总结实施步骤
从特殊到一般
活动经验
谢谢观看,再见.
引入问题,探讨方法.
函数零点
存在定理
函数
单调性
函数零点个数
方程实数解的个数
利用函数研究方程的近似解.
上节课
?
?
?
?
本节课
问题1:我们已经知道函数 f?x?=?lnx+2x?6在(2,3) 内存在一个零点,如何求出这个零点?
?
引入问题,探讨方法.
追问1:你能求出函数?f?x?=?lnx+2x?6零点的精确值吗?
?
只需求出满足一定精确度的近似解.
例如:当精确度为????时,只需|近似值?精确值| ?
问题1:我们已经知道函数?f?x?=?lnx+2x?6在(2,3)内存在一个零点,如何求出这个零点?
?
引入问题,探讨方法.
追问2:当精确度为0.5时,你能得到一个符合要求的零点的近似值吗?
|近似值?精确值| <0.5.
?
x0
2.5
0.5
0.5
1
2.5到零点
x0的距离
<0.5
?
2.5
为区间?(a,b)?的中点.
?
a+b2
?
|2.5? x0| <0.5.
?
问题1:我们已经知道函数?f?x?=?lnx+2x?6在(2,3)内存在一个零点,如何求出这个零点?
?
引入问题,探讨方法.
追问3:当精确度为0.5时,3可以看作零点的一个近似值吗?为什么?
零点x0在(2,2.5)内还是(2.5,3) 内?如何确定?
?
f?2?f?(2.5)
?
f?2.5?f?(3)
?
可以
x0
2.5
0.5
0.5
1
f?2<0
?
f?3>0
?
f?2.5
?
≈?0.084
?
零点x0∈(2.5,3).
?
|3? x0| <0.5.
?
<0
?
问题1:我们已经知道函数?f?x?=?lnx+2x?6在(2,3)内存在一个零点,如何求出这个零点?
?
引入问题,探讨方法.
追问4:当精确度缩小到0.01时,为了得到函数零点的近似值,至少需要将零点所
在区间缩小到什么程度?
我们可以采取怎样的办法来
逐步缩小零点所在区间?
x0
2.5
0.5
0.5
1
区间长度<0.01.
?
重复计算区间中点和区间端点函数值乘积的符号.
x
d < 0.01
a
b
x0
小于0.01
问题2:当精确度为0.01时,求
函数?f?x?=?lnx+2x?6零点的近似值.
?
解决问题,实施方法.
{5940675A-B579-460E-94D1-54222C63F5DA}零点所
在区间
中点
的值
中点函数
近似值
(2,3)
2.5
?0.084
?
f?2.5?f?(3)<0
?
(2.5,3)
2.75
0.512
f?2.5?f?(2.75)<0
?
(2.5,2.75)
问题2:当精确度为0.01时,求
函数?f?x?=?lnx+2x?6零点的近似值.
?
解决问题,实施方法.
零点存在定理
问题2:当精确度为0.01时,求
函数?f?x?=?lnx+2x?6零点的近似值.
?
解决问题,实施方法.
区间长度<0.01
?
该区间内任意一个数都可以作为零点的近似值.
问题2:当精确度为0.01时,求
函数?f?x?=?lnx+2x?6零点的近似值.
?
解决问题,实施方法.
区间长度<0.01
?
为了方便,可以把区间端点作为零点的近似值.
近似值x =?2.53125或2.5390625.
?
方程?lnx+2x?6?=?0的近似解.
?
问题3:在问题2中,我们用怎样
的方法求函数?f?x?=?lnx+2x?6零点
的近似值?这种方法适用于哪些函数?
?
总结提炼,归纳方法.
不断将零点所在区间一分为二,使得区间的两个端点逐步逼近零点.
理论基础:零点存在定理.
适用条件:某区间上图象连续不断,区间端点函
数值的乘积符号为负.
问题3:在问题2中,我们用怎样
的方法求函数?f?x?=?lnx+2x?6零点
的近似值?这种方法适用于哪些函数?
?
总结提炼,归纳方法.
归纳出二分法的定义:
对于在区间[a,b]上图象连续不断且 f?a?f?(b)<0
的函数?y?=?f?x?,通过不断地把它的零点所在区间一分为二,使所得区间的两个端点逐步逼近零点,进而
得到零点近似值的方法叫做二分法.
?
问题4:根据求函数?f?x?=?lnx+2x?6?零点的近似值的过程,你能提炼出给定精确度????,用二分法求函数?y?=?f?x?零点????0的近似值的一般步骤吗?
?
总结提炼,归纳方法.
回顾求函数?f?x?=?lnx+2x?6
零点x0的近似值的过程:
?
总结提炼,归纳方法.
1. 确定初始区间.
f?2?f?(3)<0?x0?∈ (2,3) .
?
回顾求函数?f?x?=?lnx+2x?6
零点x0的近似值的过程:
?
总结提炼,归纳方法.
2. 不断缩小区间
通过重复计算区间中点和区间端点函数值乘积的符号,将零点所在区间逐次减半地缩小.
(1)计算区间中点;
(2)计算中点函数值;
(3)计算区间中点和区间端点函数值乘积的符号;
(4)确定零点所在区间.
区间长度<精确度时结束重复操作.
?
回顾求函数?f?x?=?lnx+2x?6
零点x0的近似值的过程:
?
总结提炼,归纳方法.
1. 确定初始区间.
2. 不断缩小区间.
3. 得到近似值.
f?2?f?(3)<0?x0?∈ (2,3) .
?
通过重复计算区间重点中点和区间端点函数值乘积的符号,将零点所在区间逐次减半地缩小.
当零点所在区间的长度小于精确度时,把区间的一
个端点作为零点的近似值.
总结提炼,归纳方法.
小结:给定精确度????,用二分法求函数?y?=?f?x?零点 x0 的近似值的一般步骤.
?
1. 确定零点 x0 的初始区间[a,b],验证 f?a?f?(b)<0.
?
2. 求区间 (a,b) 的中点c.
3. 计算 f (c),并进一步确定零点所在的区间:
(1)若 f (c)?= 0 (此时 x0?=????),则????就是函数的零点;
(2)若f?a?f?(c)<0 (此时 x0?∈?(a,c) ),则令b?= c;
(3)若f?c?f?(b)<0 (此时 x0?∈?(c,b) ),则令a?= c.
?
4. 判断是否达到精确度????:若| a???b | 近似值a (或 b );否则重复步骤2~4.
?
例题实践,熟悉方法.
问题5:借助信息技术,用二分法求方程
2x+3x?7=0的近似解(精确度为0.1).
?
分析:转化为研究函数 f (x)?=2x+3x?7
零点的近似值(精确度为0.1).
?
f?1?f?(2)<0,
?
说明该函数在区间 (1,2) 内存在零点 x0.
第1步:确定零点 x0 所在的初始区间.
例题实践,熟悉方法.
问题5:借助信息技术,用二分法求方程
2x+3x?7=0的近似解(精确度为0.1).
?
分析:转化为研究函数 f (x)?=2x+3x?7
零点的近似解(精确度为0.1).
?
(1,2).
第1步:确定零点 x0 所在的初始区间.
第2步:求区间中点.
取 (1,2) 的中点 x1 =1.5.
?
例题实践,熟悉方法.
问题5:借助信息技术,用二分法求方程
2x+3x?7=0的近似解(精确度为0.1).
?
分析:转化为研究函数 f (x)?=2x+3x?7
零点的近似解(精确度为0.1).
?
(1,2).
第1步:确定零点 x0 所在的初始区间.
第2步:求区间中点.
取 (1,2) 的中点 x1 =1.5.
?
第3步:计算中点函数值,进一步确定零点
所在区间.
f?1.5≈0.33,
?
所以 f?1?f?(1.5)<0,所以 x0 ∈(1,1.5).
?
f?1<0,
?
例题实践,熟悉方法.
问题5:借助信息技术,用二分法求方程
2x+3x?7=0的近似解(精确度为0.1).
?
分析:转化为研究函数 f (x)?=2x+3x?7
零点的近似解(精确度为0.1).
?
(1,2).
第1步:确定零点 x0 所在的初始区间.
第2步:求区间中点.
取 (1,2) 的中点 x1 =1.5.
?
第3步:计算中点函数值,进一步确定零点
所在区间.
f?1?f?(1.5)<0?x0 ∈(1,1.5).
?
第4步:判断是否达到精确度0.1.
|1.5?1|=0.5>0.1
?
没有达到.
重复步骤2~4.
例题实践,熟悉方法.
问题5:借助信息技术,用二分法求方程
2x+3x?7=0的近似解(精确度为0.1).
?
分析:转化为研究函数 f (x)?=2x+3x?7
零点的近似解(精确度为0.1).
?
……
第2步:求区间中点.
取 (1,1.5) 的中点 x2 =1.25.
?
第3步:计算中点函数值,进一步确定零点所在区间.
f?1.25≈?0.87,
?
因为 f?1.25?f?(1.5)<0,
所以 x0 ∈(1.25,1.5).
?
例题实践,熟悉方法.
问题5:借助信息技术,用二分法求方程
2x+3x?7=0的近似解(精确度为0.1).
?
分析:转化为研究函数 f (x)?=2x+3x?7
零点的近似解(精确度为0.1).
?
……
第2步:求区间中点.
取 (1,1.5) 的中点 x2 =1.25.
?
第3步:计算中点函数值,进一步确定零点所在区间.
f?1.25?f?(1.5)<0?x0 ∈(1.25,1.5).
?
第4步:判断是否达到精确度0.1.
没有达到.
重复步骤2~4.
例题实践,熟悉方法.
问题5:借助信息技术,用二分法求方程
2x+3x?7=0的近似解(精确度为0.1).
?
分析:转化为研究函数 f (x)?=2x+3x?7
零点的近似解(精确度为0.1).
?
……
第2步:求区间中点.
取 (1,1.5) 的中点 x2 =1.25.
?
第3步:计算中点函数值,进一步确定零点所在区间.
f?1.25?f?(1.5)<0?x0 ∈(1.25,1.5).
?
第4步:判断是否达到精确度0.1.
没有达到.
同理可得,x0 ∈(1.375,1.5) ,x0 ∈(1.375,1.4375).
?
例题实践,熟悉方法.
问题5:借助信息技术,用二分法求方程
2x+3x?7=0的近似解(精确度为0.1).
?
分析:转化为研究函数 f (x)?=2x+3x?7
零点的近似解(精确度为0.1).
?
……
同理可得,x0 ∈(1.375,1.5) ,x0 ∈(1.375,1.4375).
?
由于|1.375 ? 1.4375| = 0.0625 < 0.1,所以原方程的近似解可取为1.375(或1.4375).
?
执行“二分法”的实施步骤.
课堂小结
用二分法求方程的近似解
函数零点
方程的解
?
?
不断缩小零点所在区间
函数思想
极限思想
算法思想
总结实施步骤
从特殊到一般
活动经验
谢谢观看,再见.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
