鲁教版七年级上册 第五章 位置与坐标——平面直角坐标系与坐标变化 (含答案)
文档属性
| 名称 | 鲁教版七年级上册 第五章 位置与坐标——平面直角坐标系与坐标变化 (含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
平面直角坐标系
【知识梳理】
平面直角坐标系
1、有序数对:有顺序的两个数a与b组成的数对。
记作(a
,b)
注意先后顺序
2、平面直角坐标系
在平面内画两条互相垂直、原点重合的数轴就组成平面直角坐标系(如图1)
3、构成坐标系的各种名称
(1)坐标轴:水平的数轴称为x轴或横轴,习惯上取向右为正方向;竖直的数轴称为y轴或纵轴,取向上方向为正方向,两坐标轴的交点为平面直角坐标系的原点。x轴和y轴统称为坐标轴
(2)坐标:平面内任意一点P,过点P分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a,b分别叫做点P的横坐标、纵坐标,有序数对(a,b)叫做点P的坐标,记作:P(a,b),如图2.
①表示点的坐标时,约定横坐标写在前,纵坐标写在后,中间“,”隔开.
②点P(a,b)中,|a|表示点到y轴的距离;|b|表示点到x轴的距离.
③对于坐标平面内任意一点都有唯一的一对有序数对(x,y)和它对应,反过来对于任意一对有序数对,在坐标平面内都有唯一的一点与它对应,也就是说,坐标平面内的点与有序数对是一一对应的
象限:建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成如图所示的Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分,分别叫做第一象限、第二象限、第三象限和第四象限,如图3
.①坐标轴x轴与y轴上的点(包括原点)不属于任何象限.
②按方位来说:第一象限在坐标平面的右上方,第二象限在左上方,第三象限在左下方,第四象限在右下方.
【例题1】在平面直角坐标系中,描出下列各点A(4,3),B(-2,3),C(-4,1),D(2,-2)
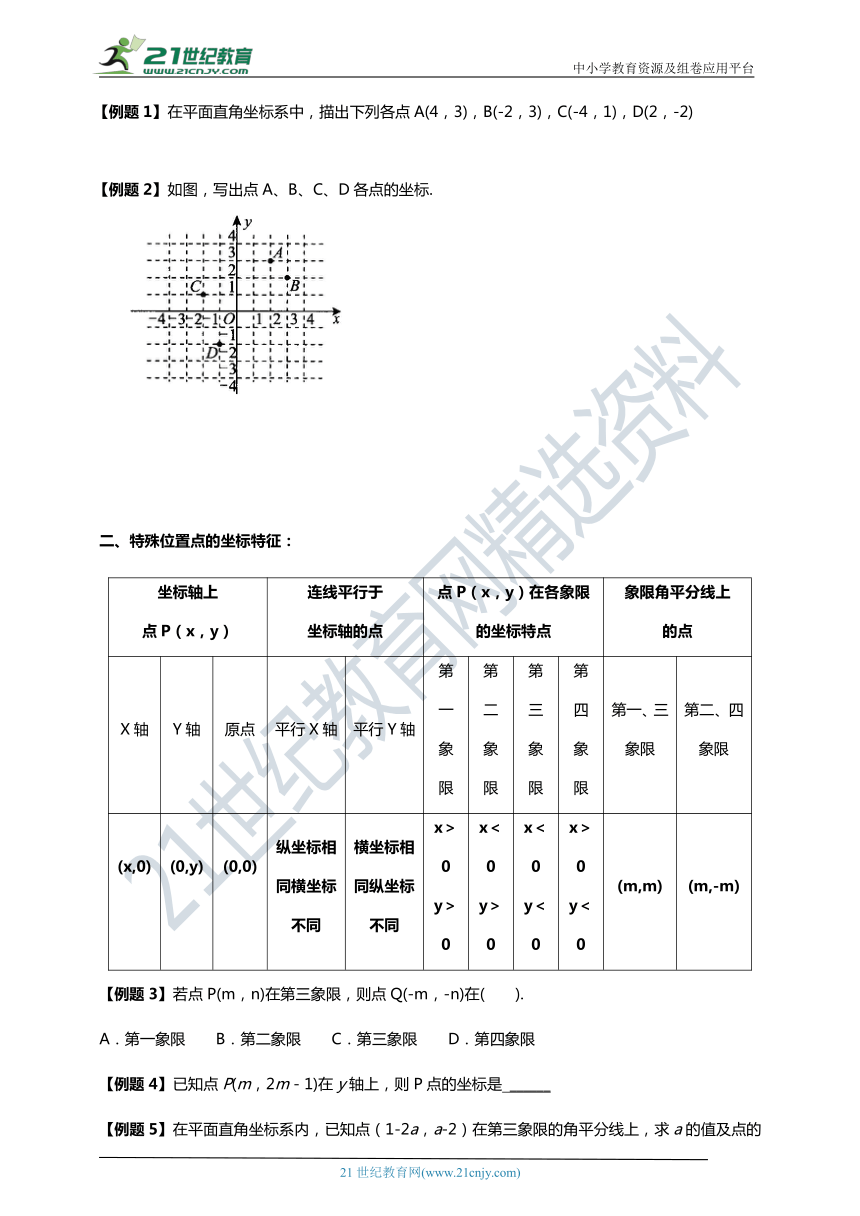
【例题2】如图,写出点A、B、C、D各点的坐标.
二、特殊位置点的坐标特征:
坐标轴上点P(x,y)
连线平行于坐标轴的点
点P(x,y)在各象限的坐标特点
象限角平分线上的点
X轴
Y轴
原点
平行X轴
平行Y轴
第一象限
第二象限
第三象限
第四象限
第一、三象限
第二、四象限
(x,0)
(0,y)
(0,0)
纵坐标相同横坐标不同
横坐标相同纵坐标不同
x>0y>0
x<0y>0
x<0y<0
x>0y<0
(m,m)
(m,-m)
【例题3】若点P(m,n)在第三象限,则点Q(-m,-n)在(
).
第一象限
B.第二象限
C.第三象限
D.第四象限
【例题4】已知点P(m,2m-1)在y轴上,则P点的坐标是
______
【例题5】在平面直角坐标系内,已知点(1-2a,a-2)在第三象限的角平分线上,求a的值及点的坐标?
三、坐标平面内的点到坐标轴的距离
点到x轴的距离为纵坐标的绝对值
点到y轴的距离为横坐标的绝对值
如P(x,y)到x轴的距离为|y|,到y轴的距离为|x|
【例题6】在平面直角坐标系中,如果点A既在x轴的上方,又在y轴的左边,且距离x轴,y轴分别为5个单位长度和4个单位长度,那么点A的坐标为(
).
A.(5,-4)
B.(4,-5)
C.(-5,4)
D.(-4,5)
四、对称点的坐标特征:
点P关于轴的对称点为,
即横坐标不变,纵坐标变为相反数;
点P关于轴的对称点为,
即纵坐标不变,横坐标变为相反数;
点P关于原点的对称点为,即横、纵坐标都变为相反数;
【例题7】
已知A(4,b),B(a,-2),若A,B关于x轴对称,则a=_____,b=_____;若A,B关于y轴对称,则a=_____,b=_____;若若A,B关于原点对称,则a=_______,b=_________;
【类型题一、对称点的坐标】
1、点A(1,-2)关于x轴对称的点的坐标是______;点A关于y轴对称的点坐标为______
2、点(,1)关于轴对称的点的坐标是(
).
A.
(,)
B.
(2,1)
C.(2,)
D.
(1,)
3、点A(1-a,5),B(3,b)关于y轴对称,则a+b=______
4、如果点和点关于轴对称,则的值为______
5、若点A(2,a)关于x轴的对称点是B(b,-3)则ab的值是_______
【类型题二、各象限内的点的坐标】
1、若点P(a,b)在第四象限,则点M(b-a,a-b)在(
)
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
2、点P(x,y)位于x轴下方,y轴左侧,且=2
,=4,点P的坐标是(
)
A.(4,2)
B.(-2,-4)
C.(-4,-2)
D.(2,4)
3、在平面直角坐标系中,点一定在
( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4、若点P(a,b)在第三象限,则点P'(-a,-b+1)在第
象限
5、若点A(m,n)在第二象限,则点(|m|,-n)在第____象限;
【类型题三、点到坐标轴的距离】
1、若轴上的点到轴的距离为3,则点的坐标为(
)
?
(A)(3,0)?
(B)(0,3)?
(C)(3,0)或(-3,0)
(D)(0,3)或(0,-3)
2、点P的横坐标是-3,且到x轴的距离为5,则P点的坐标是(
)
A.
(5,-3)或(-5,-3)
B.
(-3,5)或(-3,-5)
C.
(-3,5)
D.
(-3,-5)
3、已知点p的坐标为(2-a,3a+6),且点P到两坐标轴的距离相等,求a的值及点P的坐标.
【类型题四、坐标轴上的点的坐标】
1、点(,)在轴上,则点坐标为(
).
(A)(0,-4)
(B)(4,0)
(C)(-2,0)
(D)(0,-2)
2、点P(m+3,m+1)在x轴上,则P点坐标为(
)
A.(0,-2)
B.(2,0)
C.(4,0)
D.(0,-4)
3、已知点M在轴上,则点M的坐标为_____
【类型题五、平行于坐标轴的直线上的点的坐标】
1、已知点P(2m+1,3m)和点Q(2,?3),且直线PQ∥y轴,求m的值及PQ的长。
2、已知点A(m,?2),B(3,m?1),且直线AB∥x轴,则m的值是______
3、到x轴的距离等于2的点组成的图形是
(
)
A.
过点(0,2)且与x轴平行的直线
B.
过点(2,0)且与y轴平行的直线
C.
过点(0,-2)且与x轴平行的直线
D.
分别过(0,2)和(0,-2)且与x轴平行的两条直线
【类型题六、应用】
1、一个长方形在平面直角坐标系中三个顶点的坐标为(-1,-1),(-1,2),(3,-1),则第四个顶点的坐标为(
)
?
(A)(2,2)?
(B)(3,2)?
(C)(3,3)?
(D)(2,3)
2、在平面直角坐标系中,A,B,C三点的坐标分别为(0,0),(0,-5),(-2,-2),以这三点为平行四边形的三个顶点,则第四个顶点不可能在第_______象限
3、已知点M在y轴上,纵坐标为5,点P(3,-2),则△OMP的面积是_______
4、已知点A(0,1),B(0
,2),点C在x轴上,且,则点C的坐标??
???.
5、如图,给出格点△ABC.
(1)写出△ABC各顶点的坐标;
(2)求出此时三角形的周长。
(3)求三角形面积
6、如图,已知在平面直角坐标系中,S△ABC=24,OA=OB,BC
=12,求△ABC三个顶点的坐标.
【课后检测】
1、若y轴上的点P到x轴的距离为3,则点P的坐标是
(?????
)
?
A、(3,0)?
B、(0,3)??
C、(3,0)或(-3,0)?
D、(0,3)或(0,-3)
2、若点P(x,y)在第三象限,且点P到x轴的距离为3,到y轴的距离为2,则点P的坐标是(??
??)
?
A.(-2,-3)??
B.(-2,3)?
C.(2,-3)?
D.(2,3)
3、已知点P(x+3,x﹣4)在x轴上,则x的值为(
)
A.3???????
B.4?
????????
C.﹣3?????????
D.﹣4
4、若点A(m,n)在第二象限,那么点B(-m,│n│)在(??
)
??
A.第一象限??????
B.第二象限;????
C.第三象限??????
D.第四象限
5、一个长方形在平面直角坐标系中,三个顶点的坐标分别是(-1,-1)、(-1,2)、(3,-1),则第四个顶点的坐标是(?????
)
A.(2,2)??
?
B.(3,2)????
C.(3,3)????
D.(2,3)
6、点A(1-x,5)、B(3,y)关于y轴对称,那么x+y
=
???.
7、已知P(0,a)在y轴的负半轴上,则Q()在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
8、若点M(a-2,2a+3)是x轴上的点,则a的值是
9、已知点P的坐标(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是
.
10、在直角坐标系中,画出三角形AOB,使A、B两点的坐标分别为A(-2,-4),B(-6,-2).试求出三角形AOB的面积.
参考答案
例题1:略。在图中描出点即可
例题2:A(2,3),B(3,2),C(-2,1),D(-1,-2)
例题3:A
例题4:(0,-1)
例题5:答案
得出,将带入点中,得出点的坐标为
例题6:D
例题7:
类型题一
A
9
-4
6
类型题二
B
B
B
第一象限
第四象限
类型题三
C
B
答案:或
解析:由题意得,,解得或,将和分别代入,求出P点的坐标为
类型题四
C
B
类型题五
答案:
D
类型题六
B
第一象限
(1)
答案:
解析:在方格纸中构造直角三角形,利用勾股定理得出
答案:
解析:在方格纸中,将补成一个长方形,用长方形面积,减去周围3个直角三角形的面积,即可得出的面积
答案:
解析:的面积为24,,得出,
课后检测
D
A
B
A
B
9
B
或
答案:10
解析:在方格纸中,将补成一个长方形,用长方形面积,减去周围3个直角三角形的面积,即可得出的面积
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
平面直角坐标系
【知识梳理】
平面直角坐标系
1、有序数对:有顺序的两个数a与b组成的数对。
记作(a
,b)
注意先后顺序
2、平面直角坐标系
在平面内画两条互相垂直、原点重合的数轴就组成平面直角坐标系(如图1)
3、构成坐标系的各种名称
(1)坐标轴:水平的数轴称为x轴或横轴,习惯上取向右为正方向;竖直的数轴称为y轴或纵轴,取向上方向为正方向,两坐标轴的交点为平面直角坐标系的原点。x轴和y轴统称为坐标轴
(2)坐标:平面内任意一点P,过点P分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a,b分别叫做点P的横坐标、纵坐标,有序数对(a,b)叫做点P的坐标,记作:P(a,b),如图2.
①表示点的坐标时,约定横坐标写在前,纵坐标写在后,中间“,”隔开.
②点P(a,b)中,|a|表示点到y轴的距离;|b|表示点到x轴的距离.
③对于坐标平面内任意一点都有唯一的一对有序数对(x,y)和它对应,反过来对于任意一对有序数对,在坐标平面内都有唯一的一点与它对应,也就是说,坐标平面内的点与有序数对是一一对应的
象限:建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成如图所示的Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分,分别叫做第一象限、第二象限、第三象限和第四象限,如图3
.①坐标轴x轴与y轴上的点(包括原点)不属于任何象限.
②按方位来说:第一象限在坐标平面的右上方,第二象限在左上方,第三象限在左下方,第四象限在右下方.
【例题1】在平面直角坐标系中,描出下列各点A(4,3),B(-2,3),C(-4,1),D(2,-2)
【例题2】如图,写出点A、B、C、D各点的坐标.
二、特殊位置点的坐标特征:
坐标轴上点P(x,y)
连线平行于坐标轴的点
点P(x,y)在各象限的坐标特点
象限角平分线上的点
X轴
Y轴
原点
平行X轴
平行Y轴
第一象限
第二象限
第三象限
第四象限
第一、三象限
第二、四象限
(x,0)
(0,y)
(0,0)
纵坐标相同横坐标不同
横坐标相同纵坐标不同
x>0y>0
x<0y>0
x<0y<0
x>0y<0
(m,m)
(m,-m)
【例题3】若点P(m,n)在第三象限,则点Q(-m,-n)在(
).
第一象限
B.第二象限
C.第三象限
D.第四象限
【例题4】已知点P(m,2m-1)在y轴上,则P点的坐标是
______
【例题5】在平面直角坐标系内,已知点(1-2a,a-2)在第三象限的角平分线上,求a的值及点的坐标?
三、坐标平面内的点到坐标轴的距离
点到x轴的距离为纵坐标的绝对值
点到y轴的距离为横坐标的绝对值
如P(x,y)到x轴的距离为|y|,到y轴的距离为|x|
【例题6】在平面直角坐标系中,如果点A既在x轴的上方,又在y轴的左边,且距离x轴,y轴分别为5个单位长度和4个单位长度,那么点A的坐标为(
).
A.(5,-4)
B.(4,-5)
C.(-5,4)
D.(-4,5)
四、对称点的坐标特征:
点P关于轴的对称点为,
即横坐标不变,纵坐标变为相反数;
点P关于轴的对称点为,
即纵坐标不变,横坐标变为相反数;
点P关于原点的对称点为,即横、纵坐标都变为相反数;
【例题7】
已知A(4,b),B(a,-2),若A,B关于x轴对称,则a=_____,b=_____;若A,B关于y轴对称,则a=_____,b=_____;若若A,B关于原点对称,则a=_______,b=_________;
【类型题一、对称点的坐标】
1、点A(1,-2)关于x轴对称的点的坐标是______;点A关于y轴对称的点坐标为______
2、点(,1)关于轴对称的点的坐标是(
).
A.
(,)
B.
(2,1)
C.(2,)
D.
(1,)
3、点A(1-a,5),B(3,b)关于y轴对称,则a+b=______
4、如果点和点关于轴对称,则的值为______
5、若点A(2,a)关于x轴的对称点是B(b,-3)则ab的值是_______
【类型题二、各象限内的点的坐标】
1、若点P(a,b)在第四象限,则点M(b-a,a-b)在(
)
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
2、点P(x,y)位于x轴下方,y轴左侧,且=2
,=4,点P的坐标是(
)
A.(4,2)
B.(-2,-4)
C.(-4,-2)
D.(2,4)
3、在平面直角坐标系中,点一定在
( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4、若点P(a,b)在第三象限,则点P'(-a,-b+1)在第
象限
5、若点A(m,n)在第二象限,则点(|m|,-n)在第____象限;
【类型题三、点到坐标轴的距离】
1、若轴上的点到轴的距离为3,则点的坐标为(
)
?
(A)(3,0)?
(B)(0,3)?
(C)(3,0)或(-3,0)
(D)(0,3)或(0,-3)
2、点P的横坐标是-3,且到x轴的距离为5,则P点的坐标是(
)
A.
(5,-3)或(-5,-3)
B.
(-3,5)或(-3,-5)
C.
(-3,5)
D.
(-3,-5)
3、已知点p的坐标为(2-a,3a+6),且点P到两坐标轴的距离相等,求a的值及点P的坐标.
【类型题四、坐标轴上的点的坐标】
1、点(,)在轴上,则点坐标为(
).
(A)(0,-4)
(B)(4,0)
(C)(-2,0)
(D)(0,-2)
2、点P(m+3,m+1)在x轴上,则P点坐标为(
)
A.(0,-2)
B.(2,0)
C.(4,0)
D.(0,-4)
3、已知点M在轴上,则点M的坐标为_____
【类型题五、平行于坐标轴的直线上的点的坐标】
1、已知点P(2m+1,3m)和点Q(2,?3),且直线PQ∥y轴,求m的值及PQ的长。
2、已知点A(m,?2),B(3,m?1),且直线AB∥x轴,则m的值是______
3、到x轴的距离等于2的点组成的图形是
(
)
A.
过点(0,2)且与x轴平行的直线
B.
过点(2,0)且与y轴平行的直线
C.
过点(0,-2)且与x轴平行的直线
D.
分别过(0,2)和(0,-2)且与x轴平行的两条直线
【类型题六、应用】
1、一个长方形在平面直角坐标系中三个顶点的坐标为(-1,-1),(-1,2),(3,-1),则第四个顶点的坐标为(
)
?
(A)(2,2)?
(B)(3,2)?
(C)(3,3)?
(D)(2,3)
2、在平面直角坐标系中,A,B,C三点的坐标分别为(0,0),(0,-5),(-2,-2),以这三点为平行四边形的三个顶点,则第四个顶点不可能在第_______象限
3、已知点M在y轴上,纵坐标为5,点P(3,-2),则△OMP的面积是_______
4、已知点A(0,1),B(0
,2),点C在x轴上,且,则点C的坐标??
???.
5、如图,给出格点△ABC.
(1)写出△ABC各顶点的坐标;
(2)求出此时三角形的周长。
(3)求三角形面积
6、如图,已知在平面直角坐标系中,S△ABC=24,OA=OB,BC
=12,求△ABC三个顶点的坐标.
【课后检测】
1、若y轴上的点P到x轴的距离为3,则点P的坐标是
(?????
)
?
A、(3,0)?
B、(0,3)??
C、(3,0)或(-3,0)?
D、(0,3)或(0,-3)
2、若点P(x,y)在第三象限,且点P到x轴的距离为3,到y轴的距离为2,则点P的坐标是(??
??)
?
A.(-2,-3)??
B.(-2,3)?
C.(2,-3)?
D.(2,3)
3、已知点P(x+3,x﹣4)在x轴上,则x的值为(
)
A.3???????
B.4?
????????
C.﹣3?????????
D.﹣4
4、若点A(m,n)在第二象限,那么点B(-m,│n│)在(??
)
??
A.第一象限??????
B.第二象限;????
C.第三象限??????
D.第四象限
5、一个长方形在平面直角坐标系中,三个顶点的坐标分别是(-1,-1)、(-1,2)、(3,-1),则第四个顶点的坐标是(?????
)
A.(2,2)??
?
B.(3,2)????
C.(3,3)????
D.(2,3)
6、点A(1-x,5)、B(3,y)关于y轴对称,那么x+y
=
???.
7、已知P(0,a)在y轴的负半轴上,则Q()在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
8、若点M(a-2,2a+3)是x轴上的点,则a的值是
9、已知点P的坐标(2-a,3a+6),且点P到两坐标轴的距离相等,则点P的坐标是
.
10、在直角坐标系中,画出三角形AOB,使A、B两点的坐标分别为A(-2,-4),B(-6,-2).试求出三角形AOB的面积.
参考答案
例题1:略。在图中描出点即可
例题2:A(2,3),B(3,2),C(-2,1),D(-1,-2)
例题3:A
例题4:(0,-1)
例题5:答案
得出,将带入点中,得出点的坐标为
例题6:D
例题7:
类型题一
A
9
-4
6
类型题二
B
B
B
第一象限
第四象限
类型题三
C
B
答案:或
解析:由题意得,,解得或,将和分别代入,求出P点的坐标为
类型题四
C
B
类型题五
答案:
D
类型题六
B
第一象限
(1)
答案:
解析:在方格纸中构造直角三角形,利用勾股定理得出
答案:
解析:在方格纸中,将补成一个长方形,用长方形面积,减去周围3个直角三角形的面积,即可得出的面积
答案:
解析:的面积为24,,得出,
课后检测
D
A
B
A
B
9
B
或
答案:10
解析:在方格纸中,将补成一个长方形,用长方形面积,减去周围3个直角三角形的面积,即可得出的面积
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
