沪教版(上海)数学高一下册-5.3 三角函数诱导公式 课件(17张PPT)
文档属性
| 名称 | 沪教版(上海)数学高一下册-5.3 三角函数诱导公式 课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 81.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 00:00:00 | ||
图片预览




文档简介
三角函数·诱导公式
一. 复习回顾诱导公式一:
sin(k·360°+α)=sinα,cos(k·360°+α)=cosα,
tan(k·360°+α)=tanα,cot(k·360°+α)=cotα.
(k∈Z)
终边相同的角的同一个三角函数的值相等.
二.提出问题:1.试求出sin2016°的值
由公式一,引出新的问题:
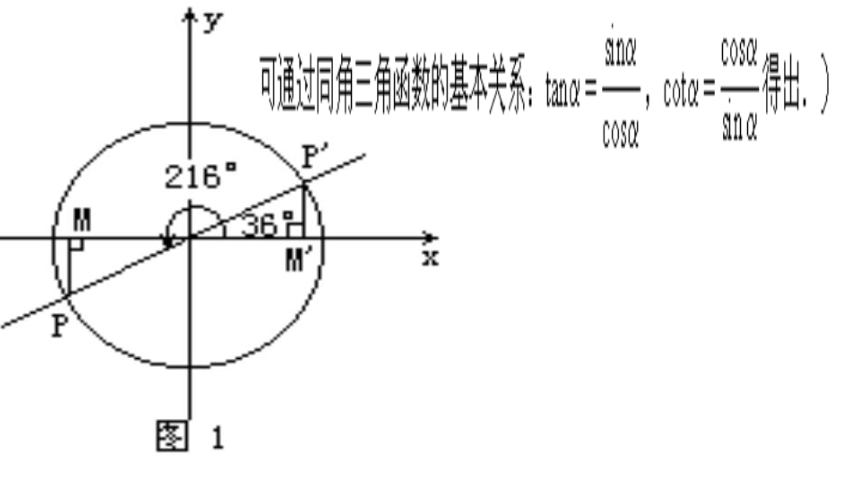
sin2016°=sin(5×360°×216°)=sin216°=?
分析
三.通过师生共同分析问题,得出诱导公式二:
sin(180°+α)=-sinα,cos(180°+α)=-cosα,
tan(180°+α)=tanα,cot(180°+α)=cotα
分析:任意角的三角函数值问题,可以由公式一化为0°~360°之间角的三角函数值问题;180°~270°之间角的三角函数值,又可通过诱导公式二化为0°~90°之间角的三角函数值,从而得出函数值;那么90°~180°、270°~360°之间的角的三角函数值问题,能否转化为0°~90°之间角的三角函数值来求出解答?
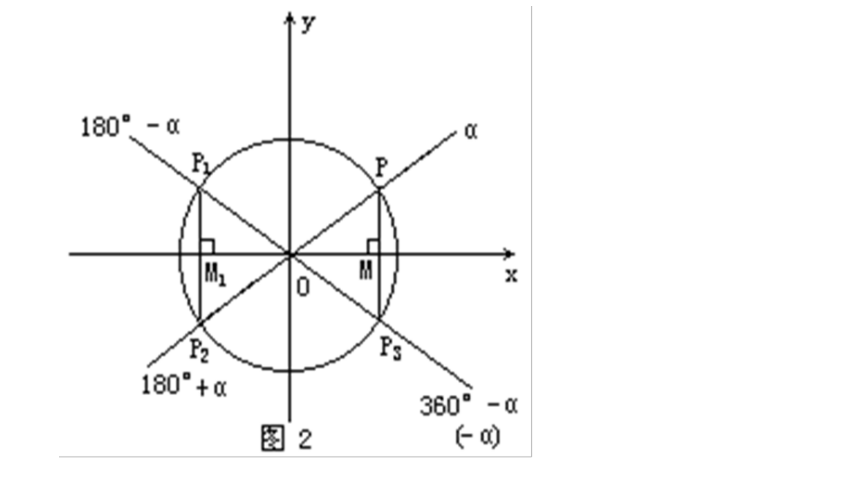
四.论证推导得出新知:
诱导公式三:
sin(-α)=-sinα,cos(-α)=cosα,
tan(-α)=-tanα,cot(-α)=-cotα
诱导公式四:
sin(180°-α)=sinα,cos(180°-α)=-cosα,
tan(180°-α)=-tanα,cot(180°-α)=-cotα.
诱导公式五:
sin(360°-α)=-sinα,cos(360°-α)=cosα,
tan(360°-α)=-tanα,cot(360°-α)=-cotα.
α为任意角时,公式二仍然成立.类似于公式二的推证方法,可以证明公式三也成立.而180°-α可以写成180°+(-α),360°-α又与-α角终边相同,容易推出,对任意角α,公式三、四、五也都成立.验证过程由同学们在课下完成.
k·360°+α(k∈Z),-α,180°±α,360°-α的三角函数值,等于α的同名三角函数值,前面加上一个把α看成锐角时原函数值的符号。
由于把α看作锐角时,k·360°+α,180°±α,-α,360°-α均可看作由x轴出发加或减α得到的,所以这五组诱导公式又可称为“水平诱导”公式.按如下方法记忆:
水平诱导名不变;符号看象限.
五.巩固练习1.
练习2.
tan(-α)
练习2.
tan(-α).
练习3.证明:
六及时小结.
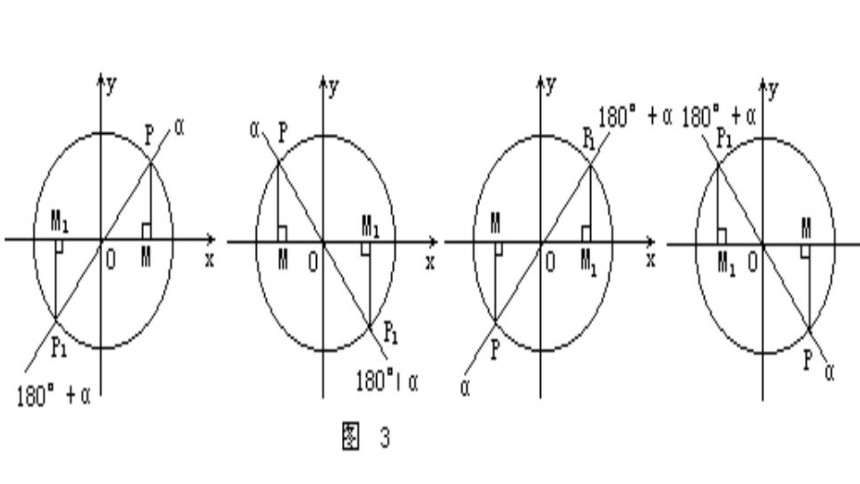
诱导公式(二)~(五)的推导方法类似,应抓住角的终边位置对称(关于原点、y轴、x轴对称)的特点及三角函数的数量关系、同角三角函数的关系.
记忆公式,要把握五组公式的结构特征:
(1)函数名称关系:函数名相同;
(2)符号规律:公式右边的符号为把α视为锐角时,角k·360°+α(k∈Z),-α、180°±α,360°-α所在象限的原三角函数值的符号.(回顾图2-7)
记忆:水平诱导名不变;符号看象限.
应用:(1)计算求值.步骤可简单记为:负化正,正化主,主化锐角可查表.(2)化简证明.要分析题目的三个结构——代数结构、三角结构和角的结构.
课堂练习:课本P158练习第3题.
课外题:课本P163习题十三第4.(1)~(4),第5题.
一. 复习回顾诱导公式一:
sin(k·360°+α)=sinα,cos(k·360°+α)=cosα,
tan(k·360°+α)=tanα,cot(k·360°+α)=cotα.
(k∈Z)
终边相同的角的同一个三角函数的值相等.
二.提出问题:1.试求出sin2016°的值
由公式一,引出新的问题:
sin2016°=sin(5×360°×216°)=sin216°=?
分析
三.通过师生共同分析问题,得出诱导公式二:
sin(180°+α)=-sinα,cos(180°+α)=-cosα,
tan(180°+α)=tanα,cot(180°+α)=cotα
分析:任意角的三角函数值问题,可以由公式一化为0°~360°之间角的三角函数值问题;180°~270°之间角的三角函数值,又可通过诱导公式二化为0°~90°之间角的三角函数值,从而得出函数值;那么90°~180°、270°~360°之间的角的三角函数值问题,能否转化为0°~90°之间角的三角函数值来求出解答?
四.论证推导得出新知:
诱导公式三:
sin(-α)=-sinα,cos(-α)=cosα,
tan(-α)=-tanα,cot(-α)=-cotα
诱导公式四:
sin(180°-α)=sinα,cos(180°-α)=-cosα,
tan(180°-α)=-tanα,cot(180°-α)=-cotα.
诱导公式五:
sin(360°-α)=-sinα,cos(360°-α)=cosα,
tan(360°-α)=-tanα,cot(360°-α)=-cotα.
α为任意角时,公式二仍然成立.类似于公式二的推证方法,可以证明公式三也成立.而180°-α可以写成180°+(-α),360°-α又与-α角终边相同,容易推出,对任意角α,公式三、四、五也都成立.验证过程由同学们在课下完成.
k·360°+α(k∈Z),-α,180°±α,360°-α的三角函数值,等于α的同名三角函数值,前面加上一个把α看成锐角时原函数值的符号。
由于把α看作锐角时,k·360°+α,180°±α,-α,360°-α均可看作由x轴出发加或减α得到的,所以这五组诱导公式又可称为“水平诱导”公式.按如下方法记忆:
水平诱导名不变;符号看象限.
五.巩固练习1.
练习2.
tan(-α)
练习2.
tan(-α).
练习3.证明:
六及时小结.
诱导公式(二)~(五)的推导方法类似,应抓住角的终边位置对称(关于原点、y轴、x轴对称)的特点及三角函数的数量关系、同角三角函数的关系.
记忆公式,要把握五组公式的结构特征:
(1)函数名称关系:函数名相同;
(2)符号规律:公式右边的符号为把α视为锐角时,角k·360°+α(k∈Z),-α、180°±α,360°-α所在象限的原三角函数值的符号.(回顾图2-7)
记忆:水平诱导名不变;符号看象限.
应用:(1)计算求值.步骤可简单记为:负化正,正化主,主化锐角可查表.(2)化简证明.要分析题目的三个结构——代数结构、三角结构和角的结构.
课堂练习:课本P158练习第3题.
课外题:课本P163习题十三第4.(1)~(4),第5题.
