沪教版(上海)数学高一下册-5.3 同角三角比的关系应用课件(15张PPT)
文档属性
| 名称 | 沪教版(上海)数学高一下册-5.3 同角三角比的关系应用课件(15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 193.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 10:20:15 | ||
图片预览


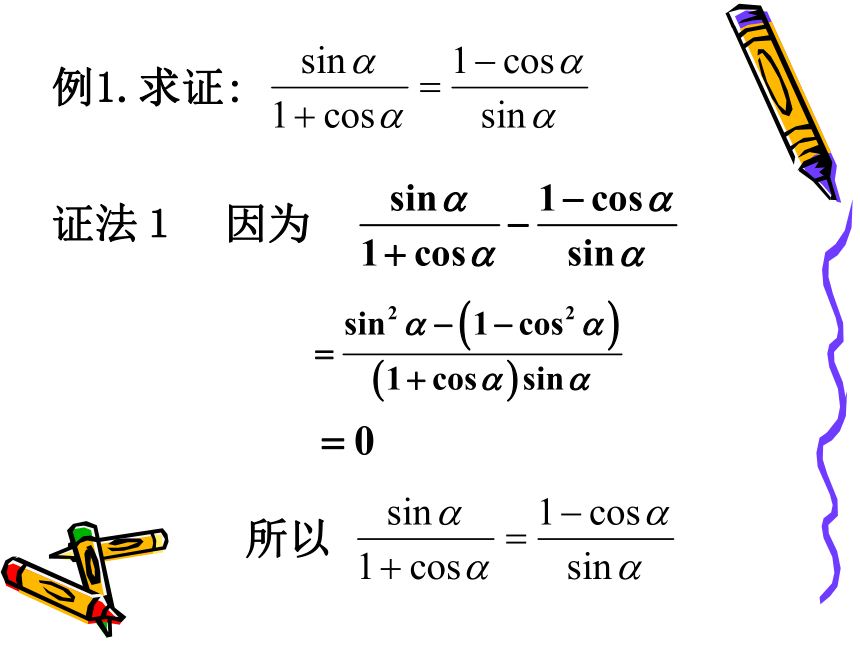
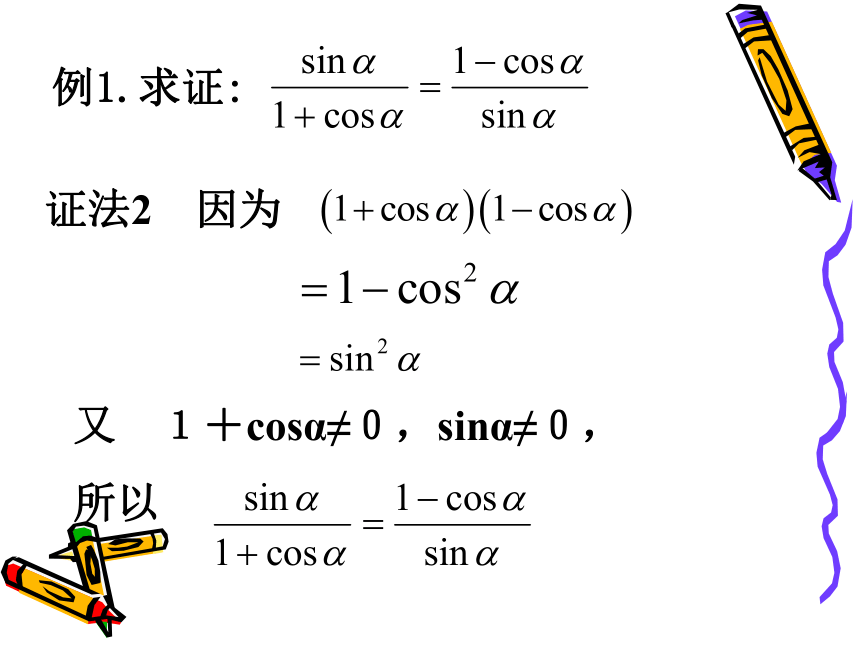


文档简介
同角三角比的关系应用
三角恒等式的证明
复习:同角三角比的基本关系式
平方关系:
商数关系:
倒数关系:
例1.求证:
证法1 因为
所以
例1.求证:
证法2 因为
又 1+cosα≠0,sinα≠0,
所以
例1.求证:
思考:可否从左式证到右式, 你有办法吗?
证法3:
例1.求证:
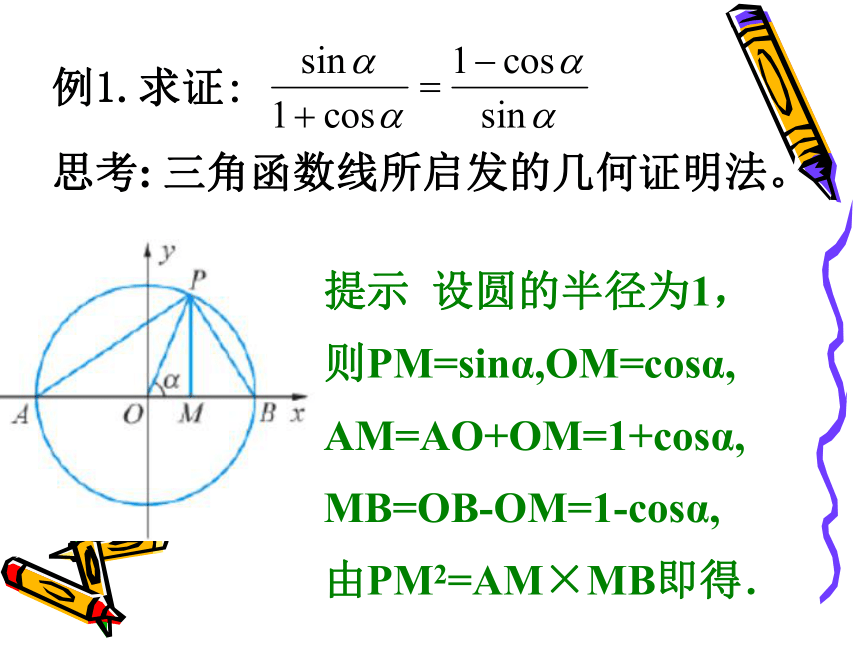
思考: 三角函数线所启发的几何证明法。
提示 设圆的半径为1,
则PM=sinα,OM=cosα,
AM=AO+OM=1+cosα,
MB=OB-OM=1-cosα,
由PM2=AM×MB即得.
证明方法
应用:利用同角三角比关系式证明三角恒等式
(1)综合法:?已知到结论。
左?右,右?左,左右归一;
(2)作差法:A-B = 0 A = B;
(3)定义法:三角比定义应用;
(4)转化命题法:?证明其等价命题;
(5)几何法等.
1.求证:
sin4α-cos4α=sin2α-cos2α;
证明:因为sin4α-cos4α
= (sin2α+cos2α) (sin2α-cos2α)
= sin2α-cos2α,
所以sin4α-cos4α=sin2α-cos2α.
练习
2.求证:
tan2αsin2α=tan2α-sin2α.
证明:因为tan2α-sin2α
所以tan2αsin2α=tan2α-sin2α.
练习
小结:利用“同角三角比关系” 证明恒等式
掌握方法、了解思路、善用公式。
证明方法
应用:利用同角三角比关系式证明三角恒等式
(1)综合法:?已知到结论。
左?右,右?左,左右归一;
(2)作差法:A-B = 0 A = B;
(3)定义法:三角比定义应用;
(4)转化命题法:?证明其等价命题;
(5)几何法等.
了解思路
一角二名三结构。转化思想方法,利用三角公式进行化名,化角,使等式两端化“异”为“同”。
善用公式:正用、逆用、变形用。
求证:
三角恒等式的证明
复习:同角三角比的基本关系式
平方关系:
商数关系:
倒数关系:
例1.求证:
证法1 因为
所以
例1.求证:
证法2 因为
又 1+cosα≠0,sinα≠0,
所以
例1.求证:
思考:可否从左式证到右式, 你有办法吗?
证法3:
例1.求证:
思考: 三角函数线所启发的几何证明法。
提示 设圆的半径为1,
则PM=sinα,OM=cosα,
AM=AO+OM=1+cosα,
MB=OB-OM=1-cosα,
由PM2=AM×MB即得.
证明方法
应用:利用同角三角比关系式证明三角恒等式
(1)综合法:?已知到结论。
左?右,右?左,左右归一;
(2)作差法:A-B = 0 A = B;
(3)定义法:三角比定义应用;
(4)转化命题法:?证明其等价命题;
(5)几何法等.
1.求证:
sin4α-cos4α=sin2α-cos2α;
证明:因为sin4α-cos4α
= (sin2α+cos2α) (sin2α-cos2α)
= sin2α-cos2α,
所以sin4α-cos4α=sin2α-cos2α.
练习
2.求证:
tan2αsin2α=tan2α-sin2α.
证明:因为tan2α-sin2α
所以tan2αsin2α=tan2α-sin2α.
练习
小结:利用“同角三角比关系” 证明恒等式
掌握方法、了解思路、善用公式。
证明方法
应用:利用同角三角比关系式证明三角恒等式
(1)综合法:?已知到结论。
左?右,右?左,左右归一;
(2)作差法:A-B = 0 A = B;
(3)定义法:三角比定义应用;
(4)转化命题法:?证明其等价命题;
(5)几何法等.
了解思路
一角二名三结构。转化思想方法,利用三角公式进行化名,化角,使等式两端化“异”为“同”。
善用公式:正用、逆用、变形用。
求证:
