沪教版(上海)数学高一下册-5.3 诱导公式 课件(13张PPT)
文档属性
| 名称 | 沪教版(上海)数学高一下册-5.3 诱导公式 课件(13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 241.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 00:00:00 | ||
图片预览

文档简介
诱导公式
x
y
r=1
x
y
r=1
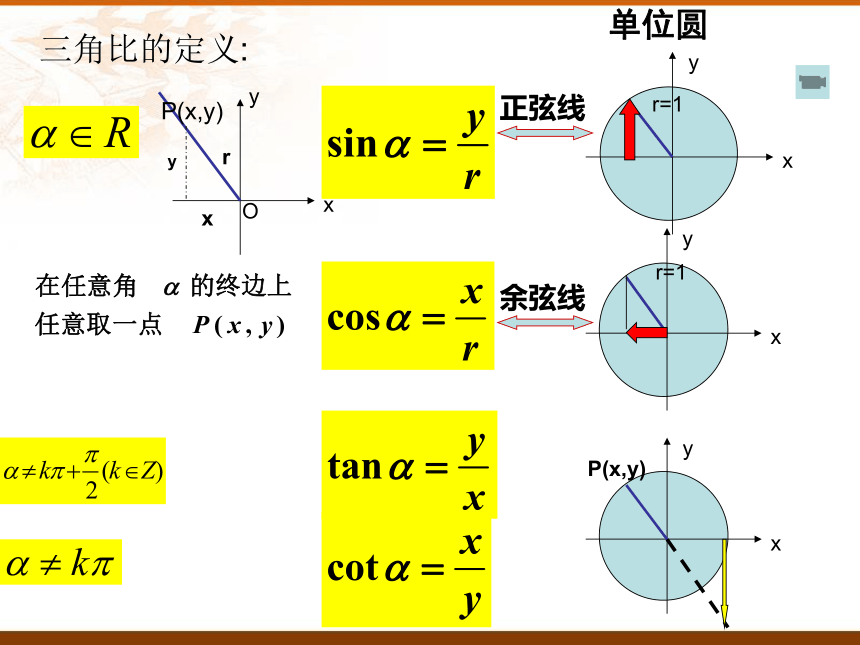
单位圆
余弦线
正弦线
x
y
P(x,y)
三角比的定义:
P(x,y)
y
O
x
y
r
x
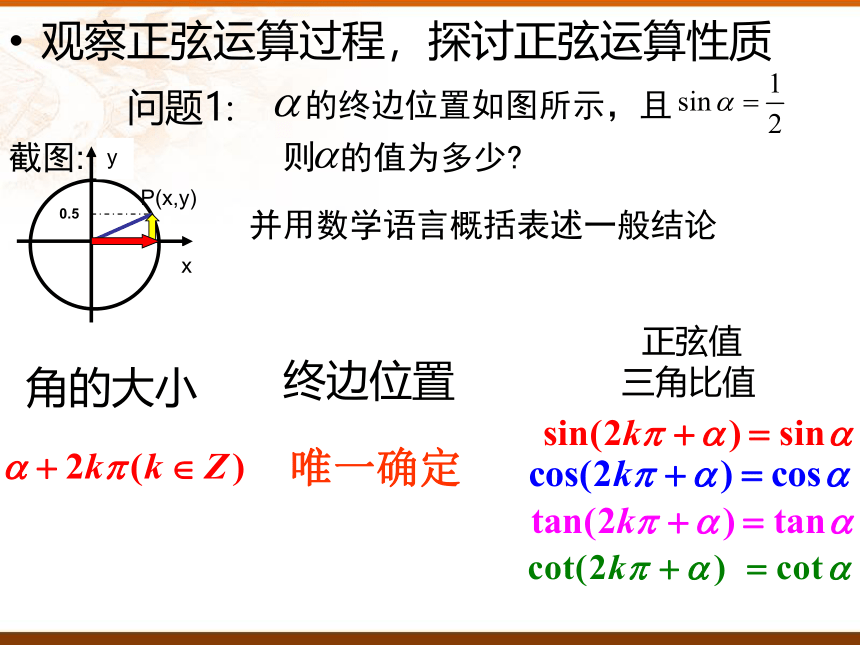
观察正弦运算过程,探讨正弦运算性质
截图:
角的大小
终边位置
正弦值
唯一确定
并用数学语言概括表述一般结论
三角比值
x
y
0.5
P(x,y)
的终边位置如图所示,且
问题1:
则
的值为多少?
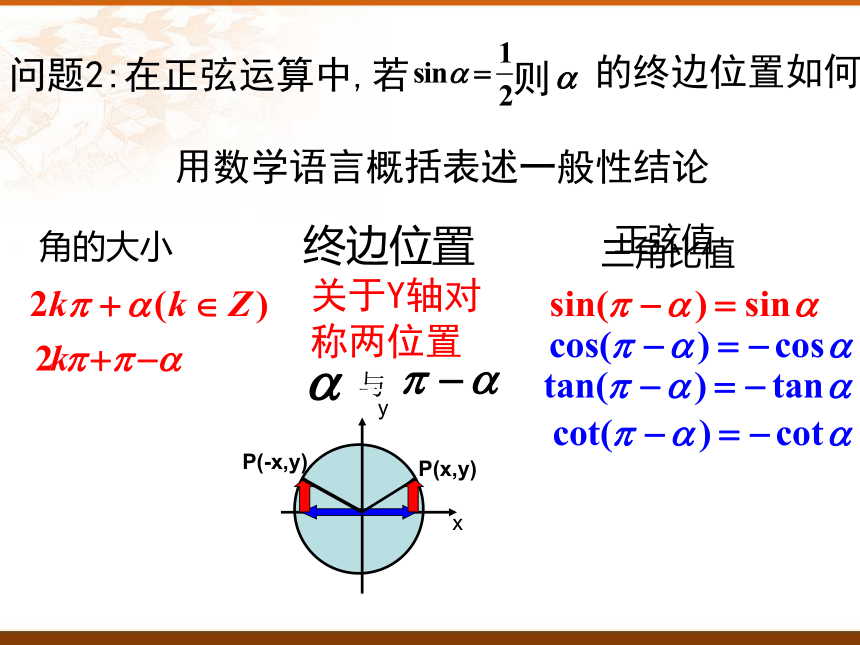
问题2:在正弦运算中,若
则
的终边位置如何?
角的大小
终边位置
正弦值
关于Y轴对称两位置
与
x
y
P(x,y)
三角比值
用数学语言概括表述一般性结论
P(-x,y)
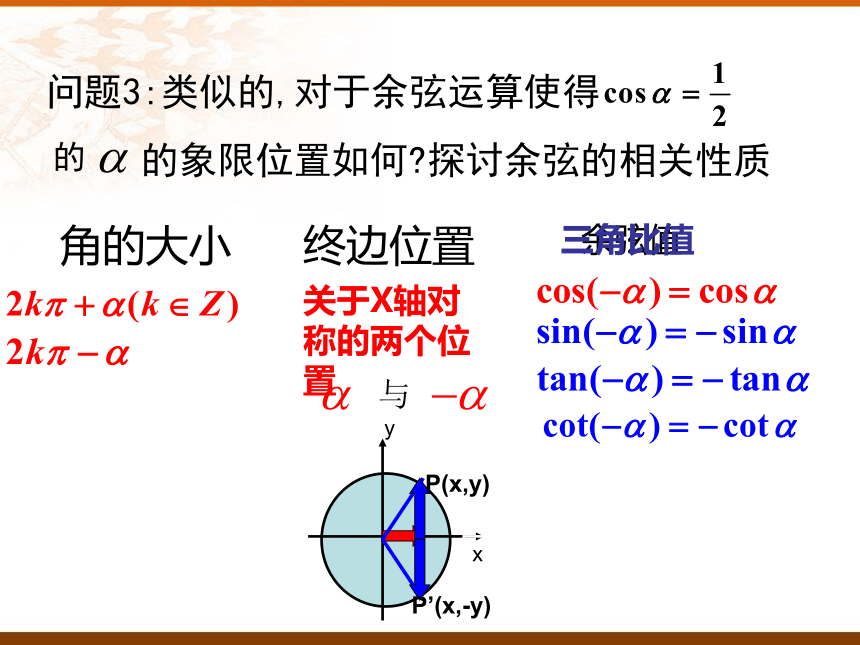
问题3:类似的,对于余弦运算使得
的
的象限位置如何?探讨余弦的相关性质
y
x
终边位置
角的大小
余弦值
关于X轴对称的两个位置
与
P(x,y)
P’(x,-y)
三角比值
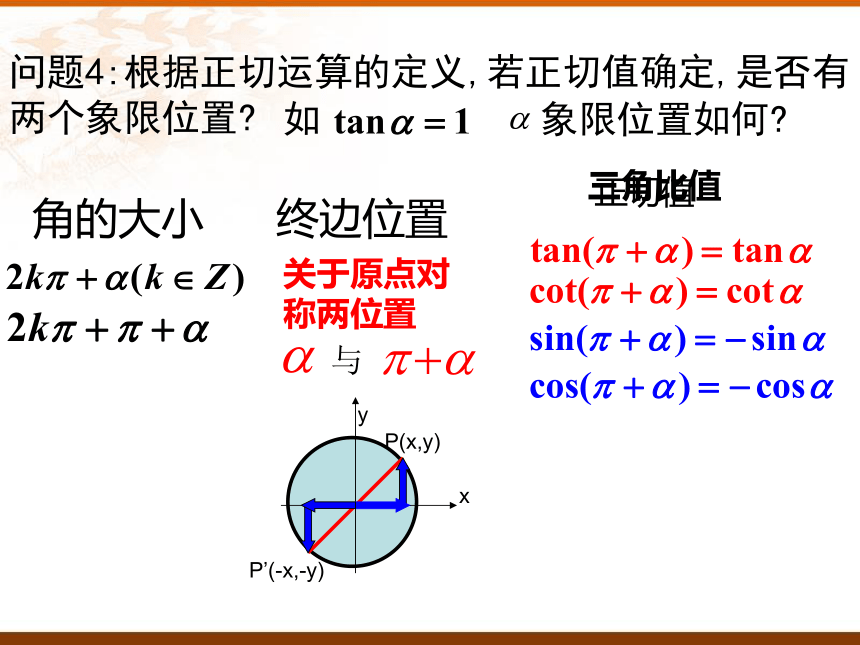
问题4:根据正切运算的定义,若正切值确定,是否有两个象限位置?
象限位置如何?
终边位置
角的大小
正切值
关于原点对称两位置
与
如
P’(-x,-y)
x
y
P(x,y)
三角比值
x
y
O
P(x , y)
x
y
x
y
x
y
一般结论
任意角的
三角比
到 的角
的三角比
诱导公式 之 同名三角比
结论反思:
1.
2. 其中
3. 将任意角的三角比诱导为
的同名三角比
小结:
根据三角比定义,借助弦线探索了
同名诱导公式;
2.诱导公式结构特点和变形对象;
4.本节课渗透了从特殊到一般,归纳分类,问题转化,数形结合等重要的数学思想方法。
3.诱导公式应用的步骤与要素;
思考题:
x
y
r=1
x
y
r=1
单位圆
余弦线
正弦线
x
y
P(x,y)
三角比的定义:
P(x,y)
y
O
x
y
r
x
观察正弦运算过程,探讨正弦运算性质
截图:
角的大小
终边位置
正弦值
唯一确定
并用数学语言概括表述一般结论
三角比值
x
y
0.5
P(x,y)
的终边位置如图所示,且
问题1:
则
的值为多少?
问题2:在正弦运算中,若
则
的终边位置如何?
角的大小
终边位置
正弦值
关于Y轴对称两位置
与
x
y
P(x,y)
三角比值
用数学语言概括表述一般性结论
P(-x,y)
问题3:类似的,对于余弦运算使得
的
的象限位置如何?探讨余弦的相关性质
y
x
终边位置
角的大小
余弦值
关于X轴对称的两个位置
与
P(x,y)
P’(x,-y)
三角比值
问题4:根据正切运算的定义,若正切值确定,是否有两个象限位置?
象限位置如何?
终边位置
角的大小
正切值
关于原点对称两位置
与
如
P’(-x,-y)
x
y
P(x,y)
三角比值
x
y
O
P(x , y)
x
y
x
y
x
y
一般结论
任意角的
三角比
到 的角
的三角比
诱导公式 之 同名三角比
结论反思:
1.
2. 其中
3. 将任意角的三角比诱导为
的同名三角比
小结:
根据三角比定义,借助弦线探索了
同名诱导公式;
2.诱导公式结构特点和变形对象;
4.本节课渗透了从特殊到一般,归纳分类,问题转化,数形结合等重要的数学思想方法。
3.诱导公式应用的步骤与要素;
思考题:
