2020-2021学年高中数学人教B版(2019)必修第三册课件:第七章 章末整合(共30张PPT)
文档属性
| 名称 | 2020-2021学年高中数学人教B版(2019)必修第三册课件:第七章 章末整合(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-18 10:55:29 | ||
图片预览











文档简介
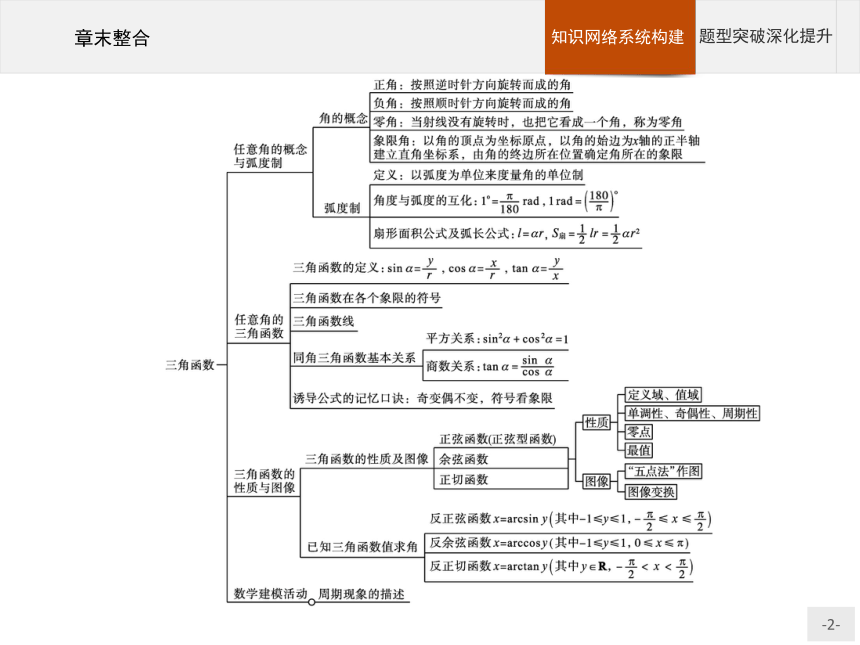
章末整合
专题一
专题二
专题三
专题四
专题一 扇形的弧长、面积公式的应用?
例1已知扇形的圆心角为α,所在圆的半径为r.
(1)若α=120°,r=6,求扇形的弧长;
(2)若扇形的周长为24,当α为多少弧度时,该扇形面积S最大?并求出最大面积.
专题一
专题二
专题三
专题四
方法规律弧度制下解决扇形相关问题的步骤
(2)分析题目的已知量和待求量,灵活选择公式.
(3)根据条件列方程(组)或建立目标函数求解.
专题一
专题二
专题三
专题四
变式训练1用一根长为10 m的绳索围成一个圆心角小于π,且半径不超过3 m的扇形场地,设扇形的半径为x m,面积为S m2.
(1)写出S关于x的函数表达式,并求出该函数的定义域;
(2)当半径x和圆心角α为多大时,所围扇形的面积S最大,并求出最大值.
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题二 利用单位圆解三角不等式?
例2利用三角函数线确定满足下列条件的角α的取值范围.
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
方法技巧 利用单位圆中的三角函数线解不等式的方法
(1)首先作出单位圆,然后根据各问题的约束条件,利用三角函数线画出角α满足条件的终边的位置.
(2)角的终边与单位圆交点的横坐标是该角的余弦值,与单位圆交点的纵坐标是该角的正弦值.
(3)写角的范围时,先抓住边界值,再注意角的范围的写法要求.
专题一
专题二
专题三
专题四
变式训练2利用三角函数线,写出满足|cos α|>|sin α|的角α的集合.
专题一
专题二
专题三
专题四
专题三 同角三角函数的基本关系式的应用?
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
名师点析 1.sin α+cos α,sin α-cos α,sin αcos α三个式子中,已知其中一个,可以求其他两个,即“知一求二”,它们之间的关系是(sin α±cos α)2=1±2sin αcos α.
2.已知tan α=m,求关于sin α,cos α的齐次式的值
解决这类问题需注意以下两点:(1)一定是关于sin α,cos α的齐次式(或能化为齐次式)的三角函数式;(2)因为cos α≠0,所以可除以cos α,这样可将被求式化为关于tan α的表示式,然后代入tan α=m的值,从而完成被求式的求值.
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题四 利用三角函数的图像与性质解题?
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
方法技巧 1.确定函数y=Asin(ωx+φ)的解析式的关键是φ的确定,常用方法有:
(1)代入法:把图像上的一个已知点代入(此时A,ω已知)或代入图像与x轴的交点求解(此时要注意交点在上升区间上还是在下降区间上).
专题一
专题二
专题三
专题四
2.求形如y=Asin(ωx+φ)+b或形如y=Acos(ωx+φ)+b(其中A≠0,ω>0,b为常数)的函数的单调区间,可以借助于正弦函数、余弦函数的单调区间,通过解不等式求得.
3.具体求解时注意两点:①要把ωx+φ看作一个整体,若ω<0,先用诱导公式将式子变形,将x的系数化为正;②在A>0,ω>0时,将“ωx+φ”代入正弦(或余弦)函数的单调区间,可以解得与之单调性一致的单调区间;当A<0,ω>0时用同样方法可以求得与正弦(余弦)函数单调性相反的单调区间.
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
规律方法三角函数最值问题的常见类型及求解方法
(1)y=asin2x+bsin x+c(a≠0),可以利用换元思想设t=sin x,转化为二次函数y=at2+bt+c求最值,t的范围需要根据定义域来确定.
(2)y=Asin(ωx+φ)+b,可先由定义域求得ωx+φ的范围,然后求得sin(ωx+φ)的范围,最后得最值.
专题一
专题二
专题三
专题四
变式训练5函数y=sin 2x+cos x的最大值为 .
专题一
专题二
专题三
专题四
专题一 扇形的弧长、面积公式的应用?
例1已知扇形的圆心角为α,所在圆的半径为r.
(1)若α=120°,r=6,求扇形的弧长;
(2)若扇形的周长为24,当α为多少弧度时,该扇形面积S最大?并求出最大面积.
专题一
专题二
专题三
专题四
方法规律弧度制下解决扇形相关问题的步骤
(2)分析题目的已知量和待求量,灵活选择公式.
(3)根据条件列方程(组)或建立目标函数求解.
专题一
专题二
专题三
专题四
变式训练1用一根长为10 m的绳索围成一个圆心角小于π,且半径不超过3 m的扇形场地,设扇形的半径为x m,面积为S m2.
(1)写出S关于x的函数表达式,并求出该函数的定义域;
(2)当半径x和圆心角α为多大时,所围扇形的面积S最大,并求出最大值.
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题二 利用单位圆解三角不等式?
例2利用三角函数线确定满足下列条件的角α的取值范围.
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
方法技巧 利用单位圆中的三角函数线解不等式的方法
(1)首先作出单位圆,然后根据各问题的约束条件,利用三角函数线画出角α满足条件的终边的位置.
(2)角的终边与单位圆交点的横坐标是该角的余弦值,与单位圆交点的纵坐标是该角的正弦值.
(3)写角的范围时,先抓住边界值,再注意角的范围的写法要求.
专题一
专题二
专题三
专题四
变式训练2利用三角函数线,写出满足|cos α|>|sin α|的角α的集合.
专题一
专题二
专题三
专题四
专题三 同角三角函数的基本关系式的应用?
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
名师点析 1.sin α+cos α,sin α-cos α,sin αcos α三个式子中,已知其中一个,可以求其他两个,即“知一求二”,它们之间的关系是(sin α±cos α)2=1±2sin αcos α.
2.已知tan α=m,求关于sin α,cos α的齐次式的值
解决这类问题需注意以下两点:(1)一定是关于sin α,cos α的齐次式(或能化为齐次式)的三角函数式;(2)因为cos α≠0,所以可除以cos α,这样可将被求式化为关于tan α的表示式,然后代入tan α=m的值,从而完成被求式的求值.
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题四 利用三角函数的图像与性质解题?
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
方法技巧 1.确定函数y=Asin(ωx+φ)的解析式的关键是φ的确定,常用方法有:
(1)代入法:把图像上的一个已知点代入(此时A,ω已知)或代入图像与x轴的交点求解(此时要注意交点在上升区间上还是在下降区间上).
专题一
专题二
专题三
专题四
2.求形如y=Asin(ωx+φ)+b或形如y=Acos(ωx+φ)+b(其中A≠0,ω>0,b为常数)的函数的单调区间,可以借助于正弦函数、余弦函数的单调区间,通过解不等式求得.
3.具体求解时注意两点:①要把ωx+φ看作一个整体,若ω<0,先用诱导公式将式子变形,将x的系数化为正;②在A>0,ω>0时,将“ωx+φ”代入正弦(或余弦)函数的单调区间,可以解得与之单调性一致的单调区间;当A<0,ω>0时用同样方法可以求得与正弦(余弦)函数单调性相反的单调区间.
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
专题一
专题二
专题三
专题四
规律方法三角函数最值问题的常见类型及求解方法
(1)y=asin2x+bsin x+c(a≠0),可以利用换元思想设t=sin x,转化为二次函数y=at2+bt+c求最值,t的范围需要根据定义域来确定.
(2)y=Asin(ωx+φ)+b,可先由定义域求得ωx+φ的范围,然后求得sin(ωx+φ)的范围,最后得最值.
专题一
专题二
专题三
专题四
变式训练5函数y=sin 2x+cos x的最大值为 .
