人教版九年级数学下册第26章:反比例函数 小结与复习(25张PPT)
文档属性
| 名称 | 人教版九年级数学下册第26章:反比例函数 小结与复习(25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 16:59:22 | ||
图片预览







文档简介
(共25张PPT)
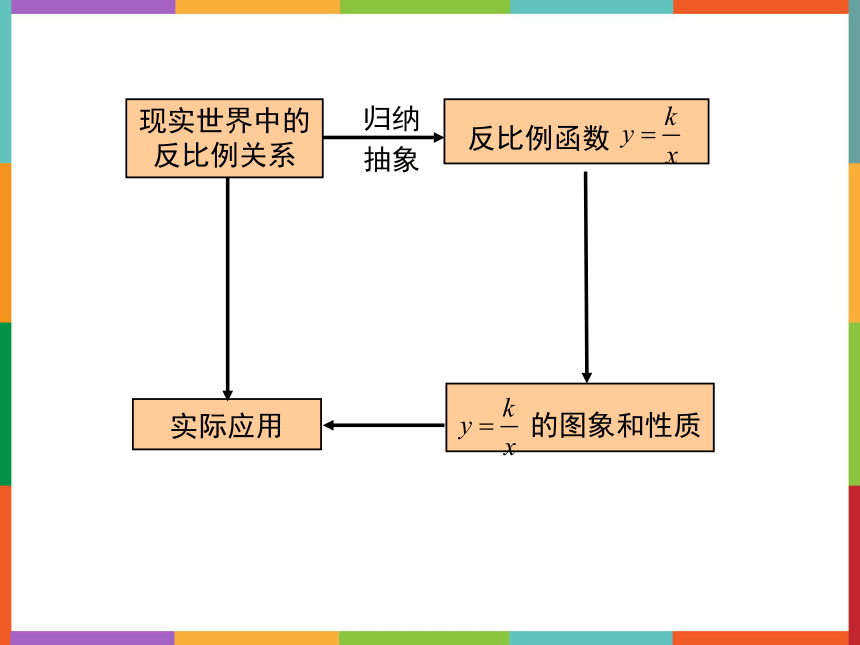
反比例函数
实际应用
现实世界中的反比例关系
反比例函数
归纳
抽象
的图象和性质
1
反比例函数的概念
2
反比例函数的图象和性质
双曲线
原点
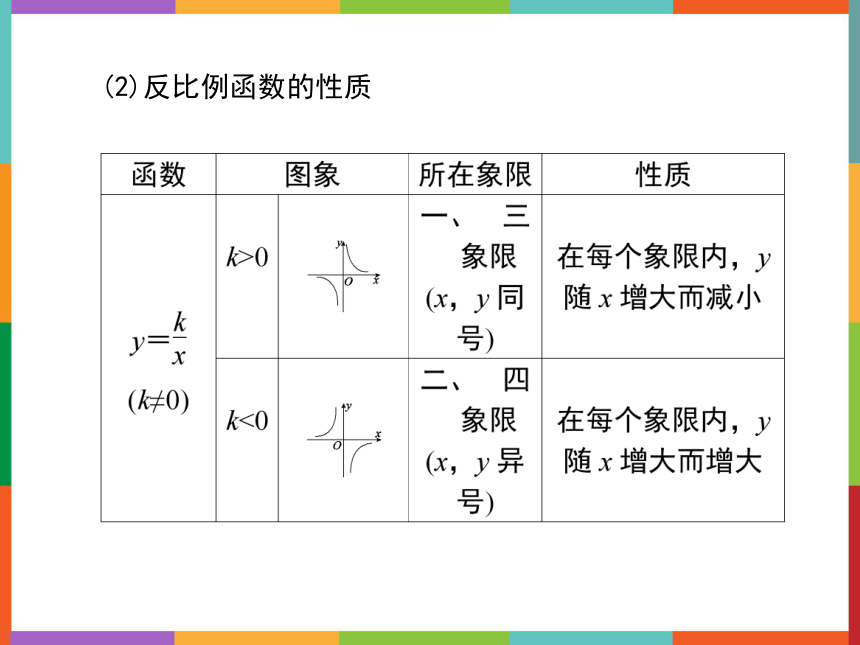
(2)反比例函数的性质
(3)反比例函数比例系数k的几何意义
k的几何意义:反比例函数图象上的点(x,y)具有两坐标之积(xy=k)为常数这一特点,即过双曲线上任意一点,向两坐标轴作垂线,两条垂线与坐标轴所围成的矩形的面积为常数|k|.
规律:过双曲线上任意一点,向两坐标轴作垂线,一条垂线与坐标轴、原点所围成的三角形的面积为常数
.
求函数解析式的方法步骤
利用待定系数法确定反比例函数:①根据两变量之间的反比例关系,设y=
;②代入图象上一个点的坐标,即x、y的一对对应值,求出k的值;③写出解析式.
反比例函数与一次函数的图象的交点的求法
求直线y=k1x+b(k≠0)和双曲线y=
的交点坐标就是解这两个函数解析式组成的方程组
3
反比例函数的应用
考点归纳
反比例函数的概念
一
命题角度:
1.
反比例函数的概念;
2.
求反比例函数的解析式.
B
反比例函数的图象和性质
二
命题角度:
反比例函数的图象与性质.
D
比较反比例函数值的大小,在同一个象限内根据反比例函数的性质比较,在不同象限内,不能按其性质比较,函数值的大小只能根据特征确定.
归纳
与反比例函数k有关的问题
三
命题角度:
反比例函数中k的几何意义.
1
利用反比例函数中k的几何意义时,要注意点的坐标与线段长之间的转化,并且利用关系式和横坐标,求各点的纵坐标是求面积的关键.
归纳
反比例函数的应用
四
命题角度:
1.
反比例函数与一次函数的综合运用.
2.
反比例函数在实际生活中的应用;
此类一次函数,反比例函数,二元一次方程组,三角形面积等知识的综合运用,其关键是理清解题思路,在直角坐标系中,求三角形或四边形面积时,常常采用分割法,把所求的图形分成几个三角形或四边形,分别求出面积后再相加.
归纳
例
病人按规定的剂量服用某种药物,测得服药后
2小时,
每毫升血液中的含药量达到最大值为
4
毫克.已知服药
后,2
小时前每毫升血液中的含药量
y(单位:毫克)与时间
x(单
位:小时)成正比例;2
小时后
y
与
x
成反比例(如图
).根
据以上信息解答下列问题:
(1)求当
0≤x≤2
时,y
与
x
的函数解析式;
(2)求当
x>2
时,y
与
x
的函数解析式;
(3)若每毫升血液中的含药量不低于
2
毫克时治疗有效,则
服药一次,治疗疾病的有效时间是多长?
考题预测
C
C
项
讲
解
一次函数与反比例函数综合应用
专
考情分析
反比例函数与一次函数结合主要考查
1.判断一次函数与反比例函数在同一坐标系中的大致图像。
2.利用函数图像确定自变量的取值范围
3.求反比例函数与一次函数解析式、点的坐标、三角形的面积等。
B
判断同一坐标系下一次函数与反比例图象
利用函数图像确定自变量的取值范围
如图,一次函数与反比例函数的图象相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围是( ).
A、x<-1
B、x>2
C、-1<x<0或x>2
D、x<-1或0<x<2
求一次函数及反比例函数的解析式
与面积有关的问题
谢谢观看
欢迎指导!
反比例函数
实际应用
现实世界中的反比例关系
反比例函数
归纳
抽象
的图象和性质
1
反比例函数的概念
2
反比例函数的图象和性质
双曲线
原点
(2)反比例函数的性质
(3)反比例函数比例系数k的几何意义
k的几何意义:反比例函数图象上的点(x,y)具有两坐标之积(xy=k)为常数这一特点,即过双曲线上任意一点,向两坐标轴作垂线,两条垂线与坐标轴所围成的矩形的面积为常数|k|.
规律:过双曲线上任意一点,向两坐标轴作垂线,一条垂线与坐标轴、原点所围成的三角形的面积为常数
.
求函数解析式的方法步骤
利用待定系数法确定反比例函数:①根据两变量之间的反比例关系,设y=
;②代入图象上一个点的坐标,即x、y的一对对应值,求出k的值;③写出解析式.
反比例函数与一次函数的图象的交点的求法
求直线y=k1x+b(k≠0)和双曲线y=
的交点坐标就是解这两个函数解析式组成的方程组
3
反比例函数的应用
考点归纳
反比例函数的概念
一
命题角度:
1.
反比例函数的概念;
2.
求反比例函数的解析式.
B
反比例函数的图象和性质
二
命题角度:
反比例函数的图象与性质.
D
比较反比例函数值的大小,在同一个象限内根据反比例函数的性质比较,在不同象限内,不能按其性质比较,函数值的大小只能根据特征确定.
归纳
与反比例函数k有关的问题
三
命题角度:
反比例函数中k的几何意义.
1
利用反比例函数中k的几何意义时,要注意点的坐标与线段长之间的转化,并且利用关系式和横坐标,求各点的纵坐标是求面积的关键.
归纳
反比例函数的应用
四
命题角度:
1.
反比例函数与一次函数的综合运用.
2.
反比例函数在实际生活中的应用;
此类一次函数,反比例函数,二元一次方程组,三角形面积等知识的综合运用,其关键是理清解题思路,在直角坐标系中,求三角形或四边形面积时,常常采用分割法,把所求的图形分成几个三角形或四边形,分别求出面积后再相加.
归纳
例
病人按规定的剂量服用某种药物,测得服药后
2小时,
每毫升血液中的含药量达到最大值为
4
毫克.已知服药
后,2
小时前每毫升血液中的含药量
y(单位:毫克)与时间
x(单
位:小时)成正比例;2
小时后
y
与
x
成反比例(如图
).根
据以上信息解答下列问题:
(1)求当
0≤x≤2
时,y
与
x
的函数解析式;
(2)求当
x>2
时,y
与
x
的函数解析式;
(3)若每毫升血液中的含药量不低于
2
毫克时治疗有效,则
服药一次,治疗疾病的有效时间是多长?
考题预测
C
C
项
讲
解
一次函数与反比例函数综合应用
专
考情分析
反比例函数与一次函数结合主要考查
1.判断一次函数与反比例函数在同一坐标系中的大致图像。
2.利用函数图像确定自变量的取值范围
3.求反比例函数与一次函数解析式、点的坐标、三角形的面积等。
B
判断同一坐标系下一次函数与反比例图象
利用函数图像确定自变量的取值范围
如图,一次函数与反比例函数的图象相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围是( ).
A、x<-1
B、x>2
C、-1<x<0或x>2
D、x<-1或0<x<2
求一次函数及反比例函数的解析式
与面积有关的问题
谢谢观看
欢迎指导!
